
First class constraint
Encyclopedia
In a constrained Hamiltonian system, a dynamical quantity is called a first class constraint if its Poisson bracket with all the other constraints vanishes on the constraint surface (the surface implicitly defined by the simultaneous vanishing of all the constraints).
, consider a symplectic manifold
M with a smooth
Hamiltonian over it (for field theories, M would be infinite-dimensional).
Suppose we have some constraints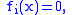
for n smooth functions
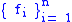
These will only be defined chartwise in general. Suppose that everywhere on the constrained set, the n derivatives of the n functions are all linearly independent and also that the Poisson bracket
s
and
all vanish on the constrained subspace. This means we can write
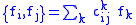
for some smooth functions
(there is a theorem showing this) and
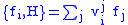
for some smooth functions
This can be done globally, using a partition of unity. Then, we say we have an irreducible first-class constraint (irreducible here is in a different sense from that used in representation theory
).
over M, with n-dimensional fiber
V. Equip this vector bundle with a connection
. Suppose too we have a smooth section f of this bundle.
Then the covariant derivative
of f with respect to the connection is a smooth linear map Δf from the tangent bundle
TM to V, which preserves the base point. Assume this linear map is right invertible (i.e. there exists a linear map g such that (Δf)g is the identity map
) for all the fibers at the zeros of f. Then, according to the implicit function theorem
, the subspace of zeros of f is a submanifold
.
The ordinary Poisson bracket
is only defined over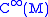 , the space of smooth functions over M. However, using the connection, we can extend it to the space of smooth sections of f if we work with the algebra bundle
, the space of smooth functions over M. However, using the connection, we can extend it to the space of smooth sections of f if we work with the algebra bundle
with the graded algebra
of V-tensors as fibers. Assume also that under this Poisson bracket,
(note that it's not true that
in general for this "extended Poisson bracket" anymore) and
on the submanifold of zeros of f (If these brackets also happen to be zero everywhere, then we say the constraints close off shell). It turns out the right invertibility condition and the commutativity of flows conditions are independent of the choice of connection. So, we can drop the connection provided we are working solely with the restricted subspace.
Since we wish to restrict ourselves to the constrained subspace only, this suggests that the Hamiltonian, or any other physical observable
, should only be defined on that subspace. Equivalently, we can look at the equivalence class of smooth functions over the symplectic manifold, which agree on the constrained subspace (the quotient algebra
by the ideal
generated by the fs, in other words).
The catch is, the Hamiltonian flows on the constrained subspace depend on the gradient of the Hamiltonian there, not its value. But there's an easy way out of this.
Look at the orbits of the constrained subspace under the action of the symplectic flows generated by the fs. This gives a local foliation
of the subspace because it satisfies integrability conditions (Frobenius theorem
). It turns out if we start with two different points on a same orbit on the constrained subspace and evolve both of them under two different Hamiltonians, respectively, which agree on the constrained subspace, then the time evolution of both points under their respective Hamiltonian flows will always lie in the same orbit at equal times. It also turns out if we have two smooth functions A1 and B1, which are constant over orbits at least on the constrained subspace (i.e. physical observables) (i.e. {A1,f}={B1,f}=0 over the constrained subspace)and another two A2 and B2, which are also constant over orbits such that A1 and B1 agrees with A2 and B2 respectively over the restrained subspace, then their Poisson brackets {A1, B1} and {A2, B2} are also constant over orbits and agree over the constrained subspace.
In general, we can't rule out "ergodic" flows (which basically means that an orbit is dense in some open set), or "subergodic" flows (which an orbit dense in some submanifold of dimension greater than the orbit's dimension). We can't have self-intersecting orbits.
For most "practical" applications of first-class constraints, we do not see such complications: the quotient space
of the restricted subspace by the f-flows (in other words, the orbit space) is well behaved enough to act as a differentiable manifold
, which can be turned into a symplectic manifold
by projecting the symplectic form of M onto it (this can be shown to be well defined). In light of the observation about physical observables mentioned earlier, we can work with this more "physical" smaller symplectic manifold, but with 2n fewer dimensions.
In general, the quotient space is a bit "nasty" to work with when doing concrete calculations (not to mention nonlocal when working with diffeomorphism constraint
s), so what is usually done instead is something similar. Note that the restricted submanifold is a bundle
(but not a fiber bundle
in general) over the quotient manifold. So, instead of working with the quotient manifold, we can work with a section
of the bundle instead. This is called gauge fixing
.
The major problem is this bundle might not have a global section in general. This is where the "problem" of global anomalies
comes in, for example. See Gribov ambiguity
. This is a flaw in quantizing gauge theories
many physicists overlooked.
What have been described are irreducible first-class constraints. Another complication is that Δf might not be right invertible on subspaces of the restricted submanifold of codimension
1 or greater (which violates the stronger assumption stated earlier in this article). This happens, for example in the cotetrad formulation of general relativity
, at the subspace of configurations where the cotetrad field and the connection form
happen to be zero over some open subset of space. Here, the constraints are the diffeomorphism constraints.
One way to get around this is this: For reducible constraints, we relax the condition on the right invertibility of Δf into this one: Any smooth function that vanishes at the zeros of f is the fiberwise contraction of f with (a non-unique) smooth section of a -vector bundle where
-vector bundle where  is the dual vector space to the constraint vector space V. This is called the regularity condition.
is the dual vector space to the constraint vector space V. This is called the regularity condition.
is the integral of a local Lagrangian
that only depends up to the first derivative of the fields. The analysis of more general cases, while possible is more complicated. When going over to the Hamiltonian formalism, we find there are constraints. Recall that in the action formalism, there are on shell and off shell configurations. The constraints that hold off shell are called primary constraints while those that only hold on shell are called secondary constraints.
g. Assume also that the parameter τ describing the trajectory of the particle is arbitrary (i.e. we insist upon reparametrization invariance). Then, its symplectic space
is the cotangent bundle
T*S with the canonical symplectic form ω. If we coordinatize T * S by its position x in the base manifold S and its position within the cotangent space p, then we have a constraint
The Hamiltonian H is, surprisingly enough, H = 0. In light of the observation that the Hamiltonian is only defined up to the equivalence class of smooth functions agreeing on the constrained subspace, we can use a new Hamiltonian H'=f instead. Then, we have the interesting case where the Hamiltonian is the same as a constraint! See Hamiltonian constraint
for more details.
Consider now the case of a Yang-Mills theory for a real simple Lie algebra L (with a negative definite Killing form
η) minimally coupled to a real scalar field σ, which transforms as an orthogonal representation ρ with the underlying vector space V under L in (d − 1) + 1 Minkowski spacetime. For l in L, we write
as
for simplicity. Let A be the L-valued connection form
of the theory. Note that the A here differs from the A used by physicists by a factor of i and g.
This article has multiple issues. Please help improve it or discuss these issues on the talk page.
It does not cite any references or sources. Please help improve it by adding citations to reliable sources. Tagged since December 2009.
It may need to be rewritten entirely to comply with Wikipedia's quality standards. Tagged since February 2009.
It may be confusing or unclear to readers. Tagged since December 2006.
This article needs attention from an expert on the subject. See the talk page for details. WikiProject Mathematics or the Mathematics Portal may be able to help recruit an expert. (November 2008)
In a constrained Hamiltonian system, a dynamical quantity is called a first class constraint if its Poisson bracket with all the other constraints vanishes on the constraint surface (the surface implicitly defined by the simultaneous vanishing of all the constraints).
Contents [hide]
1 Poisson brackets
2 Geometric theory
3 Intuitive meaning
4 Constrained Hamiltonian dynamics from a Lagrangian gauge theory
5 Examples
[edit]Poisson brackets
In Hamiltonian mechanics, consider a symplectic manifold M with a smooth Hamiltonian over it (for field theories, M would be infinite-dimensional).
Suppose we have some constraints
fi(x) = 0,
for n smooth functions
These will only be defined chartwise in general. Suppose that everywhere on the constrained set, the n derivatives of the n functions are all linearly independent and also that the Poisson brackets
{ fi, fj }
and
{ fi, H }
all vanish on the constrained subspace. This means we can write
for some smooth functions
cijk
(there is a theorem showing this) and
for some smooth functions
vij.
This can be done globally, using a partition of unity. Then, we say we have an irreducible first-class constraint (irreducible here is in a different sense from that used in representation theory).
[edit]Geometric theory
For a more elegant way, suppose given a vector bundle over M, with n-dimensional fiber V. Equip this vector bundle with a connection. Suppose too we have a smooth section f of this bundle.
Then the covariant derivative of f with respect to the connection is a smooth linear map Δf from the tangent bundle TM to V, which preserves the base point. Assume this linear map is right invertible (i.e. there exists a linear map g such that (Δf)g is the identity map) for all the fibers at the zeros of f. Then, according to the implicit function theorem, the subspace of zeros of f is a submanifold.
The ordinary Poisson bracket is only defined over , the space of smooth functions over M. However, using the connection, we can extend it to the space of smooth sections of f if we work with the algebra bundle with the graded algebra of V-tensors as fibers. Assume also that under this Poisson bracket,
{ f, f } = 0
(note that it's not true that
{ g, g } = 0
in general for this "extended Poisson bracket" anymore) and
{ f, H } = 0
on the submanifold of zeros of f (If these brackets also happen to be zero everywhere, then we say the constraints close off shell). It turns out the right invertibility condition and the commutativity of flows conditions are independent of the choice of connection. So, we can drop the connection provided we are working solely with the restricted subspace.
[edit]Intuitive meaning
What does it all mean intuitively? It means the Hamiltonian and constraint flows all commute with each other on the constrained subspace; or alternatively, that if we start on a point on the constrained subspace, then the Hamiltonian and constraint flows all bring the point to another point on the constrained subspace.
Since we wish to restrict ourselves to the constrained subspace only, this suggests that the Hamiltonian, or any other physical observable, should only be defined on that subspace. Equivalently, we can look at the equivalence class of smooth functions over the symplectic manifold, which agree on the constrained subspace (the quotient algebra by the ideal generated by the f's, in other words).
The catch is, the Hamiltonian flows on the constrained subspace depend on the gradient of the Hamiltonian there, not its value. But there's an easy way out of this.
Look at the orbits of the constrained subspace under the action of the symplectic flows generated by the f's. This gives a local foliation of the subspace because it satisfies integrability conditions (Frobenius theorem). It turns out if we start with two different points on a same orbit on the constrained subspace and evolve both of them under two different Hamiltonians, respectively, which agree on the constrained subspace, then the time evolution of both points under their respective Hamiltonian flows will always lie in the same orbit at equal times. It also turns out if we have two smooth functions A1 and B1, which are constant over orbits at least on the constrained subspace (i.e. physical observables) (i.e. {A1,f}={B1,f}=0 over the constrained subspace)and another two A2 and B2, which are also constant over orbits such that A1 and B1 agrees with A2 and B2 respectively over the restrained subspace, then their Poisson brackets {A1, B1} and {A2, B2} are also constant over orbits and agree over the constrained subspace.
In general, we[who?] can't rule out "ergodic" flows (which basically means that an orbit is dense in some open set), or "subergodic" flows (which an orbit dense in some submanifold of dimension greater than the orbit's dimension). We can't have self-intersecting orbits.
For most "practical" applications of first-class constraints, we do not see such complications: the quotient space of the restricted subspace by the f-flows (in other words, the orbit space) is well behaved enough to act as a differentiable manifold, which can be turned into a symplectic manifold by projecting the symplectic form of M onto it (this can be shown to be well defined). In light of the observation about physical observables mentioned earlier, we can work with this more "physical" smaller symplectic manifold, but with 2n fewer dimensions.
In general, the quotient space is a bit "nasty" to work with when doing concrete calculations (not to mention nonlocal when working with diffeomorphism constraints), so what is usually done instead is something similar. Note that the restricted submanifold is a bundle (but not a fiber bundle in general) over the quotient manifold. So, instead of working with the quotient manifold, we can work with a section of the bundle instead. This is called gauge fixing.
The major problem is this bundle might not have a global section in general. This is where the "problem" of global anomalies comes in, for example. See Gribov ambiguity. This is a flaw in quantizing gauge theories many physicists overlooked.
What have been described are irreducible first-class constraints. Another complication is that Δf might not be right invertible on subspaces of the restricted submanifold of codimension 1 or greater (which violates the stronger assumption stated earlier in this article). This happens, for example in the cotetrad formulation of general relativity, at the subspace of configurations where the cotetrad field and the connection form happen to be zero over some open subset of space. Here, the constraints are the diffeomorphism constraints.
One way to get around this is this: For reducible constraints, we relax the condition on the right invertibility of Δf into this one: Any smooth function that vanishes at the zeros of f is the fiberwise contraction of f with (a non-unique) smooth section of a -vector bundle where is the dual vector space to the constraint vector space V. This is called the regularity condition.
[edit]Constrained Hamiltonian dynamics from a Lagrangian gauge theory
First of all, we will assume the action is the integral of a local Lagrangian that only depends up to the first derivative of the fields. The analysis of more general cases, while possible is more complicated. When going over to the Hamiltonian formalism, we find there are constraints. Recall that in the action formalism, there are on shell and off shell configurations. The constraints that hold off shell are called primary constraints while those that only hold on shell are called secondary constraints.
[edit]Examples
Look at the dynamics of a single point particle of mass m with no internal degrees of freedom moving in a pseudo-Riemannian spacetime manifold S with metric g. Assume also that the parameter τ describing the trajectory of the particle is arbitrary (i.e. we insist upon reparametrization invariance). Then, its symplectic space is the cotangent bundle T*S with the canonical symplectic form ω. If we coordinatize T * S by its position x in the base manifold S and its position within the cotangent space p, then we have a constraint
f = m2 −g(x)−1(p,p) = 0.
The Hamiltonian H is, surprisingly enough, H = 0. In light of the observation that the Hamiltonian is only defined up to the equivalence class of smooth functions agreeing on the constrained subspace, we can use a new Hamiltonian H'=f instead. Then, we have the interesting case where the Hamiltonian is the same as a constraint! See Hamiltonian constraint for more details.
Consider now the case of a Yang-Mills theory for a real simple Lie algebra L (with a negative definite Killing form η) minimally coupled to a real scalar field σ, which transforms as an orthogonal representation ρ with the underlying vector space V under L in (d − 1) + 1 Minkowski spacetime. For l in L, we write
ρ(l)[σ]
as
l[σ]
for simplicity. Let A be the L-valued connection form of the theory. Note that the A here differs from the A used by physicists by a factor of i and also a g. This agrees with the mathematician's convention. The action S is given by
where g is the Minkowski metric, F is the curvature form
(
no is or gs!) where the second term is a formal shorthand for pretending the Lie bracket is a commutator, D is the covariant derivative
Dσ = dσ − A[σ]
and α is the orthogonal form for ρ.
I hope I have all the signs and factors right. I can't guarantee it.
What is the Hamiltonian version of this model? Well, first, we have to split A noncovariantly into a time component φ and a spatial part . Then, the resulting symplectic space has the conjugate variables σ, πσ (taking values in the underlying vector space of , the dual rep of ρ), , , φ and πφ. for each spatial point, we have the constraints, πφ=0 and the Gaussian constraint
where since ρ is an intertwiner
,
ρ' is the dualized intertwiner
(L is self-dual via η). The Hamiltonian,
Note that the last two terms are a linear combination of the Gaussian constraints and we have a whole family of (gauge equivalent)Hamiltonians parametrized by f. In fact, since the last three terms vanish for the constrained states, we can drop them.
See also Dirac bracket, second class constraints, BRST, analysis of flows
View page ratings
Rate this page
What's this?
Trustworthy
Objective
Complete
Well-written
I am highly knowledgeable about this topic (optional)
Submit ratings
Categories: Classical mechanicsTheoretical physics
YsawiresMy talkMy preferencesMy watchlistMy contributionsLog outArticleDiscussionReadEditView historyWatch
Feedback about editing
Main page
Contents
Featured content
Current events
Random article
Donate to Wikipedia
Interaction
Help
About Wikipedia
Community portal
Recent changes
Contact Wikipedia
Toolbox
What links here
Related changes
Upload file
Special pages
Permanent link
Cite this page
Rate this page
Print/export
Create a book
Download as PDF
Printable version
This page was last modified on 31 October 2010 at 21:03.
Text is available under the Creative Commons Attribution-ShareAlike License; additional terms may apply. See Terms of use for details.
Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profit organization.
Contact us
Privacy policyAbout WikipediaDisclaimersMobile view g". This agrees with the mathematician's convention. The action S is given by
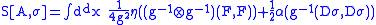
where g is the Minkowski metric, F is the curvature form
 (
(
no is or gs!) where the second term is a formal shorthand for pretending the Lie bracket is a commutator, D is the covariant derivative
and α is the orthogonal form for ρ.
I hope I have all the signs and factors right. I can't guarantee it.
What is the Hamiltonian version of this model? Well, first, we have to split A noncovariantly into a time component φ and a spatial part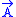 . Then, the resulting symplectic space has the conjugate variables σ, πσ (taking values in the underlying vector space of
. Then, the resulting symplectic space has the conjugate variables σ, πσ (taking values in the underlying vector space of 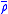 , the dual rep of ρ),
, the dual rep of ρ), 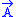 ,
, 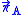 , φ and πφ. for each spatial point, we have the constraints, πφ=0 and the Gaussian constraint
, φ and πφ. for each spatial point, we have the constraints, πφ=0 and the Gaussian constraint
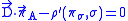
where since ρ is an intertwiner
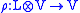 ,
,
ρ' is the dualized intertwiner
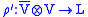
(L is self-dual via η). The Hamiltonian,
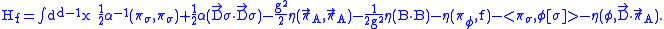
Note that the last two terms are a linear combination of the Gaussian constraints and we have a whole family of (gauge equivalent)Hamiltonians parametrized by f. In fact, since the last three terms vanish for the constrained states, we can drop them.
See also Dirac bracket
, second class constraints
, BRST
, analysis of flows
Poisson brackets
In Hamiltonian mechanicsHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, consider a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
M with a smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
Hamiltonian over it (for field theories, M would be infinite-dimensional).
Suppose we have some constraints
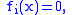
for n smooth functions
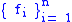
These will only be defined chartwise in general. Suppose that everywhere on the constrained set, the n derivatives of the n functions are all linearly independent and also that the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
s
- { fi, fj }
and
- { fi, H }
all vanish on the constrained subspace. This means we can write
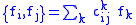
for some smooth functions
- cijk
(there is a theorem showing this) and
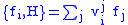
for some smooth functions
- vij.
This can be done globally, using a partition of unity. Then, we say we have an irreducible first-class constraint (irreducible here is in a different sense from that used in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
).
Geometric theory
For a more elegant way, suppose given a vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over M, with n-dimensional fiber
Fiber
Fiber is a class of materials that are continuous filaments or are in discrete elongated pieces, similar to lengths of thread.They are very important in the biology of both plants and animals, for holding tissues together....
V. Equip this vector bundle with a connection
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
. Suppose too we have a smooth section f of this bundle.
Then the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
of f with respect to the connection is a smooth linear map Δf from the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TM to V, which preserves the base point. Assume this linear map is right invertible (i.e. there exists a linear map g such that (Δf)g is the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
) for all the fibers at the zeros of f. Then, according to the implicit function theorem
Implicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
, the subspace of zeros of f is a submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
.
The ordinary Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
is only defined over
 , the space of smooth functions over M. However, using the connection, we can extend it to the space of smooth sections of f if we work with the algebra bundle
, the space of smooth functions over M. However, using the connection, we can extend it to the space of smooth sections of f if we work with the algebra bundleAlgebra bundle
In mathematics, an algebra bundle is a fiber bundle whose fibers are algebras and local trivializations respect the algebra structure. It follows that the transition functions are algebra isomorphisms...
with the graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
of V-tensors as fibers. Assume also that under this Poisson bracket,
- { f, f } = 0
(note that it's not true that
- { g, g } = 0
in general for this "extended Poisson bracket" anymore) and
- { f, H } = 0
on the submanifold of zeros of f (If these brackets also happen to be zero everywhere, then we say the constraints close off shell). It turns out the right invertibility condition and the commutativity of flows conditions are independent of the choice of connection. So, we can drop the connection provided we are working solely with the restricted subspace.
Intuitive meaning
What does it all mean intuitively? It means the Hamiltonian and constraint flows all commute with each other on the constrained subspace; or alternatively, that if we start on a point on the constrained subspace, then the Hamiltonian and constraint flows all bring the point to another point on the constrained subspace.Since we wish to restrict ourselves to the constrained subspace only, this suggests that the Hamiltonian, or any other physical observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
, should only be defined on that subspace. Equivalently, we can look at the equivalence class of smooth functions over the symplectic manifold, which agree on the constrained subspace (the quotient algebra
Quotient algebra
In mathematics, a quotient algebra, , also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence, that is an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense...
by the ideal
Ideal
-In philosophy:* Ideal , values that one actively pursues as goals* Platonic ideal, a philosophical idea of trueness of form, associated with Plato-In mathematics:* Ideal , special subsets of a ring considered in abstract algebra...
generated by the fs, in other words).
The catch is, the Hamiltonian flows on the constrained subspace depend on the gradient of the Hamiltonian there, not its value. But there's an easy way out of this.
Look at the orbits of the constrained subspace under the action of the symplectic flows generated by the fs. This gives a local foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
of the subspace because it satisfies integrability conditions (Frobenius theorem
Frobenius theorem (differential topology)
In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
). It turns out if we start with two different points on a same orbit on the constrained subspace and evolve both of them under two different Hamiltonians, respectively, which agree on the constrained subspace, then the time evolution of both points under their respective Hamiltonian flows will always lie in the same orbit at equal times. It also turns out if we have two smooth functions A1 and B1, which are constant over orbits at least on the constrained subspace (i.e. physical observables) (i.e. {A1,f}={B1,f}=0 over the constrained subspace)and another two A2 and B2, which are also constant over orbits such that A1 and B1 agrees with A2 and B2 respectively over the restrained subspace, then their Poisson brackets {A1, B1} and {A2, B2} are also constant over orbits and agree over the constrained subspace.
In general, we can't rule out "ergodic" flows (which basically means that an orbit is dense in some open set), or "subergodic" flows (which an orbit dense in some submanifold of dimension greater than the orbit's dimension). We can't have self-intersecting orbits.
For most "practical" applications of first-class constraints, we do not see such complications: the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of the restricted subspace by the f-flows (in other words, the orbit space) is well behaved enough to act as a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, which can be turned into a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
by projecting the symplectic form of M onto it (this can be shown to be well defined). In light of the observation about physical observables mentioned earlier, we can work with this more "physical" smaller symplectic manifold, but with 2n fewer dimensions.
In general, the quotient space is a bit "nasty" to work with when doing concrete calculations (not to mention nonlocal when working with diffeomorphism constraint
Diffeomorphism constraint
In theoretical physics, it is often important to study theories with the diffeomorphism symmetry such as general relativity. These theories are invariant under arbitrary coordinate transformations. Equations of motion are generally derived from the requirement that the action is stationary. There...
s), so what is usually done instead is something similar. Note that the restricted submanifold is a bundle
Bundle
Bundle or Bundling may refer to:In marketing:* Product bundling, a marketing strategy that involves offering several products for sale as one combined product...
(but not a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
in general) over the quotient manifold. So, instead of working with the quotient manifold, we can work with a section
Section (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
of the bundle instead. This is called gauge fixing
Gauge fixing
In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field...
.
The major problem is this bundle might not have a global section in general. This is where the "problem" of global anomalies
Global anomaly
In theoretical physics, a global anomaly is a type of anomaly: in this particular case, it is a quantum effect that invalidates a large gauge transformations that would otherwise be preserved in the classical theory...
comes in, for example. See Gribov ambiguity
Gribov ambiguity
In gauge theory, especially in non-abelian gauge theories, we often encounter global problems when gauge fixing. Gauge fixing means choosing a representative from each gauge orbit. The space of representatives is a submanifold and represents the gauge fixing condition. Ideally, every gauge orbit...
. This is a flaw in quantizing gauge theories
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
many physicists overlooked.
What have been described are irreducible first-class constraints. Another complication is that Δf might not be right invertible on subspaces of the restricted submanifold of codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
1 or greater (which violates the stronger assumption stated earlier in this article). This happens, for example in the cotetrad formulation of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, at the subspace of configurations where the cotetrad field and the connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
happen to be zero over some open subset of space. Here, the constraints are the diffeomorphism constraints.
One way to get around this is this: For reducible constraints, we relax the condition on the right invertibility of Δf into this one: Any smooth function that vanishes at the zeros of f is the fiberwise contraction of f with (a non-unique) smooth section of a
 -vector bundle where
-vector bundle where  is the dual vector space to the constraint vector space V. This is called the regularity condition.
is the dual vector space to the constraint vector space V. This is called the regularity condition.Constrained Hamiltonian dynamics from a Lagrangian gauge theory
First of all, we will assume the actionAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
is the integral of a local Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
that only depends up to the first derivative of the fields. The analysis of more general cases, while possible is more complicated. When going over to the Hamiltonian formalism, we find there are constraints. Recall that in the action formalism, there are on shell and off shell configurations. The constraints that hold off shell are called primary constraints while those that only hold on shell are called secondary constraints.
Examples
Look at the dynamics of a single point particle of mass m with no internal degrees of freedom moving in a pseudo-Riemannian spacetime manifold S with metricMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
g. Assume also that the parameter τ describing the trajectory of the particle is arbitrary (i.e. we insist upon reparametrization invariance). Then, its symplectic space
Symplectic space
A symplectic space is either a symplectic manifold or a symplectic vector space. The latter is a special case of the former....
is the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
T*S with the canonical symplectic form ω. If we coordinatize T * S by its position x in the base manifold S and its position within the cotangent space p, then we have a constraint
- f = m2 −g(x)−1(p,p) = 0.
The Hamiltonian H is, surprisingly enough, H = 0. In light of the observation that the Hamiltonian is only defined up to the equivalence class of smooth functions agreeing on the constrained subspace, we can use a new Hamiltonian H'=f instead. Then, we have the interesting case where the Hamiltonian is the same as a constraint! See Hamiltonian constraint
Hamiltonian constraint
In loop quantum gravity, dynamics such as time-evolutions of fields are controlled by the Hamiltonian constraint. The identity of the Hamiltonian constraint is a major open question in quantum gravity, as is extracting of physical observables from any such specific constraint.The Thiemann operator...
for more details.
Consider now the case of a Yang-Mills theory for a real simple Lie algebra L (with a negative definite Killing form
Killing form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
η) minimally coupled to a real scalar field σ, which transforms as an orthogonal representation ρ with the underlying vector space V under L in (d − 1) + 1 Minkowski spacetime. For l in L, we write
- ρ(l)[σ]
as
- l[σ]
for simplicity. Let A be the L-valued connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
of the theory. Note that the A here differs from the A used by physicists by a factor of i and g.
This article has multiple issues. Please help improve it or discuss these issues on the talk page.
It does not cite any references or sources. Please help improve it by adding citations to reliable sources. Tagged since December 2009.
It may need to be rewritten entirely to comply with Wikipedia's quality standards. Tagged since February 2009.
It may be confusing or unclear to readers. Tagged since December 2006.
This article needs attention from an expert on the subject. See the talk page for details. WikiProject Mathematics or the Mathematics Portal may be able to help recruit an expert. (November 2008)
In a constrained Hamiltonian system, a dynamical quantity is called a first class constraint if its Poisson bracket with all the other constraints vanishes on the constraint surface (the surface implicitly defined by the simultaneous vanishing of all the constraints).
Contents [hide]
1 Poisson brackets
2 Geometric theory
3 Intuitive meaning
4 Constrained Hamiltonian dynamics from a Lagrangian gauge theory
5 Examples
[edit]Poisson brackets
In Hamiltonian mechanics, consider a symplectic manifold M with a smooth Hamiltonian over it (for field theories, M would be infinite-dimensional).
Suppose we have some constraints
fi(x) = 0,
for n smooth functions
These will only be defined chartwise in general. Suppose that everywhere on the constrained set, the n derivatives of the n functions are all linearly independent and also that the Poisson brackets
{ fi, fj }
and
{ fi, H }
all vanish on the constrained subspace. This means we can write
for some smooth functions
cijk
(there is a theorem showing this) and
for some smooth functions
vij.
This can be done globally, using a partition of unity. Then, we say we have an irreducible first-class constraint (irreducible here is in a different sense from that used in representation theory).
[edit]Geometric theory
For a more elegant way, suppose given a vector bundle over M, with n-dimensional fiber V. Equip this vector bundle with a connection. Suppose too we have a smooth section f of this bundle.
Then the covariant derivative of f with respect to the connection is a smooth linear map Δf from the tangent bundle TM to V, which preserves the base point. Assume this linear map is right invertible (i.e. there exists a linear map g such that (Δf)g is the identity map) for all the fibers at the zeros of f. Then, according to the implicit function theorem, the subspace of zeros of f is a submanifold.
The ordinary Poisson bracket is only defined over , the space of smooth functions over M. However, using the connection, we can extend it to the space of smooth sections of f if we work with the algebra bundle with the graded algebra of V-tensors as fibers. Assume also that under this Poisson bracket,
{ f, f } = 0
(note that it's not true that
{ g, g } = 0
in general for this "extended Poisson bracket" anymore) and
{ f, H } = 0
on the submanifold of zeros of f (If these brackets also happen to be zero everywhere, then we say the constraints close off shell). It turns out the right invertibility condition and the commutativity of flows conditions are independent of the choice of connection. So, we can drop the connection provided we are working solely with the restricted subspace.
[edit]Intuitive meaning
What does it all mean intuitively? It means the Hamiltonian and constraint flows all commute with each other on the constrained subspace; or alternatively, that if we start on a point on the constrained subspace, then the Hamiltonian and constraint flows all bring the point to another point on the constrained subspace.
Since we wish to restrict ourselves to the constrained subspace only, this suggests that the Hamiltonian, or any other physical observable, should only be defined on that subspace. Equivalently, we can look at the equivalence class of smooth functions over the symplectic manifold, which agree on the constrained subspace (the quotient algebra by the ideal generated by the f's, in other words).
The catch is, the Hamiltonian flows on the constrained subspace depend on the gradient of the Hamiltonian there, not its value. But there's an easy way out of this.
Look at the orbits of the constrained subspace under the action of the symplectic flows generated by the f's. This gives a local foliation of the subspace because it satisfies integrability conditions (Frobenius theorem). It turns out if we start with two different points on a same orbit on the constrained subspace and evolve both of them under two different Hamiltonians, respectively, which agree on the constrained subspace, then the time evolution of both points under their respective Hamiltonian flows will always lie in the same orbit at equal times. It also turns out if we have two smooth functions A1 and B1, which are constant over orbits at least on the constrained subspace (i.e. physical observables) (i.e. {A1,f}={B1,f}=0 over the constrained subspace)and another two A2 and B2, which are also constant over orbits such that A1 and B1 agrees with A2 and B2 respectively over the restrained subspace, then their Poisson brackets {A1, B1} and {A2, B2} are also constant over orbits and agree over the constrained subspace.
In general, we[who?] can't rule out "ergodic" flows (which basically means that an orbit is dense in some open set), or "subergodic" flows (which an orbit dense in some submanifold of dimension greater than the orbit's dimension). We can't have self-intersecting orbits.
For most "practical" applications of first-class constraints, we do not see such complications: the quotient space of the restricted subspace by the f-flows (in other words, the orbit space) is well behaved enough to act as a differentiable manifold, which can be turned into a symplectic manifold by projecting the symplectic form of M onto it (this can be shown to be well defined). In light of the observation about physical observables mentioned earlier, we can work with this more "physical" smaller symplectic manifold, but with 2n fewer dimensions.
In general, the quotient space is a bit "nasty" to work with when doing concrete calculations (not to mention nonlocal when working with diffeomorphism constraints), so what is usually done instead is something similar. Note that the restricted submanifold is a bundle (but not a fiber bundle in general) over the quotient manifold. So, instead of working with the quotient manifold, we can work with a section of the bundle instead. This is called gauge fixing.
The major problem is this bundle might not have a global section in general. This is where the "problem" of global anomalies comes in, for example. See Gribov ambiguity. This is a flaw in quantizing gauge theories many physicists overlooked.
What have been described are irreducible first-class constraints. Another complication is that Δf might not be right invertible on subspaces of the restricted submanifold of codimension 1 or greater (which violates the stronger assumption stated earlier in this article). This happens, for example in the cotetrad formulation of general relativity, at the subspace of configurations where the cotetrad field and the connection form happen to be zero over some open subset of space. Here, the constraints are the diffeomorphism constraints.
One way to get around this is this: For reducible constraints, we relax the condition on the right invertibility of Δf into this one: Any smooth function that vanishes at the zeros of f is the fiberwise contraction of f with (a non-unique) smooth section of a -vector bundle where is the dual vector space to the constraint vector space V. This is called the regularity condition.
[edit]Constrained Hamiltonian dynamics from a Lagrangian gauge theory
First of all, we will assume the action is the integral of a local Lagrangian that only depends up to the first derivative of the fields. The analysis of more general cases, while possible is more complicated. When going over to the Hamiltonian formalism, we find there are constraints. Recall that in the action formalism, there are on shell and off shell configurations. The constraints that hold off shell are called primary constraints while those that only hold on shell are called secondary constraints.
[edit]Examples
Look at the dynamics of a single point particle of mass m with no internal degrees of freedom moving in a pseudo-Riemannian spacetime manifold S with metric g. Assume also that the parameter τ describing the trajectory of the particle is arbitrary (i.e. we insist upon reparametrization invariance). Then, its symplectic space is the cotangent bundle T*S with the canonical symplectic form ω. If we coordinatize T * S by its position x in the base manifold S and its position within the cotangent space p, then we have a constraint
f = m2 −g(x)−1(p,p) = 0.
The Hamiltonian H is, surprisingly enough, H = 0. In light of the observation that the Hamiltonian is only defined up to the equivalence class of smooth functions agreeing on the constrained subspace, we can use a new Hamiltonian H'=f instead. Then, we have the interesting case where the Hamiltonian is the same as a constraint! See Hamiltonian constraint for more details.
Consider now the case of a Yang-Mills theory for a real simple Lie algebra L (with a negative definite Killing form η) minimally coupled to a real scalar field σ, which transforms as an orthogonal representation ρ with the underlying vector space V under L in (d − 1) + 1 Minkowski spacetime. For l in L, we write
ρ(l)[σ]
as
l[σ]
for simplicity. Let A be the L-valued connection form of the theory. Note that the A here differs from the A used by physicists by a factor of i and also a g. This agrees with the mathematician's convention. The action S is given by
where g is the Minkowski metric, F is the curvature form
(
no is or gs!) where the second term is a formal shorthand for pretending the Lie bracket is a commutator, D is the covariant derivative
Dσ = dσ − A[σ]
and α is the orthogonal form for ρ.
I hope I have all the signs and factors right. I can't guarantee it.
What is the Hamiltonian version of this model? Well, first, we have to split A noncovariantly into a time component φ and a spatial part . Then, the resulting symplectic space has the conjugate variables σ, πσ (taking values in the underlying vector space of , the dual rep of ρ), , , φ and πφ. for each spatial point, we have the constraints, πφ=0 and the Gaussian constraint
where since ρ is an intertwiner
,
ρ' is the dualized intertwiner
(L is self-dual via η). The Hamiltonian,
Note that the last two terms are a linear combination of the Gaussian constraints and we have a whole family of (gauge equivalent)Hamiltonians parametrized by f. In fact, since the last three terms vanish for the constrained states, we can drop them.
See also Dirac bracket, second class constraints, BRST, analysis of flows
View page ratings
Rate this page
What's this?
Trustworthy
Objective
Complete
Well-written
I am highly knowledgeable about this topic (optional)
Submit ratings
Categories: Classical mechanicsTheoretical physics
YsawiresMy talkMy preferencesMy watchlistMy contributionsLog outArticleDiscussionReadEditView historyWatch
Feedback about editing
Main page
Contents
Featured content
Current events
Random article
Donate to Wikipedia
Interaction
Help
About Wikipedia
Community portal
Recent changes
Contact Wikipedia
Toolbox
What links here
Related changes
Upload file
Special pages
Permanent link
Cite this page
Rate this page
Print/export
Create a book
Download as PDF
Printable version
This page was last modified on 31 October 2010 at 21:03.
Text is available under the Creative Commons Attribution-ShareAlike License; additional terms may apply. See Terms of use for details.
Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profit organization.
Contact us
Privacy policyAbout WikipediaDisclaimersMobile view g". This agrees with the mathematician's convention. The action S is given by
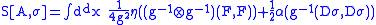
where g is the Minkowski metric, F is the curvature form
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
 (
(no is or gs!) where the second term is a formal shorthand for pretending the Lie bracket is a commutator, D is the covariant derivative
- Dσ = dσ − A[σ]
and α is the orthogonal form for ρ.
I hope I have all the signs and factors right. I can't guarantee it.
What is the Hamiltonian version of this model? Well, first, we have to split A noncovariantly into a time component φ and a spatial part
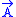 . Then, the resulting symplectic space has the conjugate variables σ, πσ (taking values in the underlying vector space of
. Then, the resulting symplectic space has the conjugate variables σ, πσ (taking values in the underlying vector space of 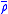 , the dual rep of ρ),
, the dual rep of ρ), 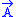 ,
, 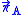 , φ and πφ. for each spatial point, we have the constraints, πφ=0 and the Gaussian constraint
, φ and πφ. for each spatial point, we have the constraints, πφ=0 and the Gaussian constraint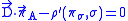
where since ρ is an intertwiner
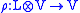 ,
,ρ' is the dualized intertwiner
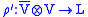
(L is self-dual via η). The Hamiltonian,
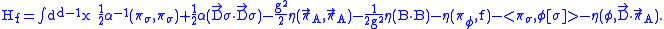
Note that the last two terms are a linear combination of the Gaussian constraints and we have a whole family of (gauge equivalent)Hamiltonians parametrized by f. In fact, since the last three terms vanish for the constrained states, we can drop them.
See also Dirac bracket
Dirac bracket
The Dirac bracket is a generalization of the Poisson bracket developed by Paul Dirac to correctly treat systems with second class constraints in Hamiltonian mechanics and canonical quantization. It is an important part of Dirac's development of Hamiltonian mechanics to handle more general Lagrangians...
, second class constraints
Second class constraints
In a constrained Hamiltonian system, a dynamical quantity is second class if its Poisson bracket with at least one constraint is nonvanishing...
, BRST
BRST
BRST may refer to:* BRST formalism and quantization in Yang-Mills theories* Big Red Switch Time , computer jargon for switching your computer off, when all other options for a more elegant shutdown have been exhausted...
, analysis of flows
Analysis of flows
In theoretical physics, an analysis of flows is the study of "gauge" or "gaugelike" "symmetries"...

