Fermi liquid
Encyclopedia
Fermi liquid theory is a theoretical model of interacting fermion
s that describes the normal state of most metal
s at sufficiently low temperatures. The interaction between the particles of the many-body system does not need to be small. The phenomenological
theory of Fermi liquids was introduced by the Soviet physicist Lev Davidovich Landau in 1956, and later developed by Alexei Abrikosov
and I. M. Khalatnikov using diagrammatic perturbation theory
. The theory explains why some of the properties of an interacting fermion system are very similar to those of the Fermi gas
(i.e. non-interacting fermions), and why other properties differ.
Important examples of where Fermi liquid theory has been successfully applied are most notably electrons in most metals and Liquid He-3. Liquid He-3
is a Fermi liquid at low temperatures (but not low enough to be in its superfluid
phase
.) He-3 is an isotope
of Helium
, with 2 proton
s, 1 neutron
and 2 electrons per atom. Because there is an odd number of fermions inside the atom, the atom itself is also a fermion. The electron
s in a normal (non-superconducting
) metal
also form a Fermi liquid, as do the nucleons (protons and neutrons) in an atomic nucleus
.
. Consider a non-interacting fermion system (a Fermi gas
), and suppose we "turn on" the interaction slowly. Landau argued that in this situation, the ground state of the Fermi gas would adiabatically transform into the ground state of the interacting system.
By Pauli's exclusion principle, the ground state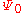
of a Fermi gas consists of fermions occupying all momentum states corresponding to momentum 
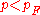with all higher momentum states unoccupied. As interaction is turned on, the spin, charge and momentum of the fermions corresponding to the occupied states remain unchanged, however, their dynamical properties, such as their mass, magnetic moment etc. are renormalized
to new values. Thus, there is a one-to-one correspondence between the elementary excitations of a Fermi gas system and a Fermi liquid system. In the context of Fermi liquids, these excitations are called "quasi-particles".
Landau quasiparticles are long-lived excitations with a lifetime
that satifies 
where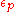 
is the Fermi energy.
For this system, the Green's function
can be written (near its poles) in the form
where
is the chemical potential
and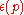
is the energy corresponding to the given momentum state.
The value
is called the quasiparticle residue and is very characteristic of Fermi liquid theory. The spectral function for the system can be directly observed via ARPES
experiment, and can be written (in the limit of low-lying excitations) in the form:
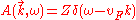
where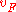
is the Fermi velocity.
Physically, we can say that a propagating fermion interacts with its surrounding in such a way that the net effect of the interactions is to make the fermion behave as a "dressed" fermion, altering its effective mass and other dynamical properties. These "dressed" fermions are what we think of as "quasiparticles".
Another important property of Fermi liquids is related to the scattering cross section for electrons. Suppose we have an electron with energy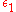
above the Fermi surface, and suppose it scatters with a particle in the Fermi sea with energy 
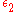. By Pauli's exclusion principle, both the particles after scattering have to lie above the Fermi surface, with energies 
Now, suppose the initial electron has energy very close to the Fermi surface 
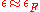Then, we have that 
also have to be very close to the Fermi surface. This reduces the phase space
volume of the possible states after scattering, and hence, by Fermi's golden rule
, the scattering cross section goes to zero. Thus we can say that the lifetime of particles at the Fermi surface goes to infinity.
, in the following sense: The system's dynamics and thermodynamics at low excitation energies and temperatures may be described by substituting the interacting fermions with non-interacting quasiparticle
s, each of which carries the same spin
, charge
and momentum
as the original particles. Physically these may be thought of as being particles whose motion is disturbed by the surrounding particles and which themselves perturb the particles in their vicinity. Each many-particle excited state of the interacting system may be described by listing all occupied momentum states, just as in the non-interacting system. As a consequence, quantities such as the heat capacity of the Fermi liquid behave qualitatively in the same way as in the Fermi gas (e.g. the heat capacity rises linearly with temperature).
of a many-particle state is not simply a sum of the single-particle energies of all occupied states. Instead, the change in energy for a given change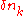
in occupation of states 
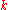contains terms both linear and quadratic in 
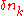(for the Fermi gas, it would only be linear, 
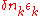, where 
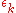denotes the single-particle energies). The linear contribution corresponds to renormalized single-particle energies, which involve, e.g., a change in the effective mass of particles. The quadratic terms correspond to a sort of "mean-field" interaction between quasiparticles, which is parameterized by so-called Landau Fermi liquid parameters and determines the behaviour of density oscillations (and spin-density oscillations) in the Fermi liquid. Still, these mean-field interactions do not lead to a scattering of quasi-particles with a transfer of particles between different momentum states.
would prevent an accurate definition of the energy).
is similar to that in the Fermi gas (where, for a given momentum, the Green's function in frequency space is a delta peak at the respective single-particle energy). The delta peak in the density-of-states is broadened (with a width given by the quasiparticle lifetime). In addition (and in contrast to the quasiparticle Green's function), its weight (integral over frequency) is suppressed by a quasiparticle weight factor
. The remainder of the total weight is in a broad "incoherent background", corresponding to the strong effects of interactions on the fermions at short time-scales.
.
. For a Fermi liquid, the resistance from this mechanism varies as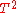
, which is often taken as an experimental check for Fermi liquid behaviour (in addition to the linear temperature-dependence of the specific heat), although it only arises in combination with the lattice.
. Although Luttinger liquids are physically the same as Fermi liquids, the restriction to one dimension gives rise to several qualitative differences such as the absence of a quasiparticle peak in the momentum dependent spectral function and the presence of spin density waves
.
Another example of such behaviour is observed at quantum critical point
s of certain second-order phase transitions, such as
Heavy fermion
criticality, Mott criticality
and high-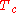
cuprate phase transitions. The ground state of such transitions is characterized by the presence of a sharp Fermi surface, although there may not be well-defined quasiparticles. That is, on approaching the critical point, it is observed that the quasiparticle residue 
Understanding the behaviour of non-Fermi liquids is an important problem in condensed matter physics. Approaches towards explaining these phenomena include the treatment of marginal Fermi liquids; attempts to understand critical points and derive scaling relations; and descriptions using emergent gauge theories
with techniques of holographic
gauge/gravity duality.
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s that describes the normal state of most metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s at sufficiently low temperatures. The interaction between the particles of the many-body system does not need to be small. The phenomenological
Phenomenology (science)
The term phenomenology in science is used to describe a body of knowledge that relates empirical observations of phenomena to each other, in a way that is consistent with fundamental theory, but is not directly derived from theory. For example, we find the following definition in the Concise...
theory of Fermi liquids was introduced by the Soviet physicist Lev Davidovich Landau in 1956, and later developed by Alexei Abrikosov
Alexei Alexeyevich Abrikosov
Alexei Alexeyevich Abrikosov is a Soviet and Russian theoretical physicist whose main contributions are in the field of condensed matter physics. He was awarded the Nobel Prize in Physics in 2003.- Biography :...
and I. M. Khalatnikov using diagrammatic perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
. The theory explains why some of the properties of an interacting fermion system are very similar to those of the Fermi gas
Fermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
(i.e. non-interacting fermions), and why other properties differ.
Important examples of where Fermi liquid theory has been successfully applied are most notably electrons in most metals and Liquid He-3. Liquid He-3
Helium-3
Helium-3 is a light, non-radioactive isotope of helium with two protons and one neutron. It is rare on Earth, and is sought for use in nuclear fusion research...
is a Fermi liquid at low temperatures (but not low enough to be in its superfluid
Superfluid
Superfluidity is a state of matter in which the matter behaves like a fluid without viscosity and with extremely high thermal conductivity. The substance, which appears to be a normal liquid, will flow without friction past any surface, which allows it to continue to circulate over obstructions and...
phase
Phase (matter)
In the physical sciences, a phase is a region of space , throughout which all physical properties of a material are essentially uniform. Examples of physical properties include density, index of refraction, and chemical composition...
.) He-3 is an isotope
Isotope
Isotopes are variants of atoms of a particular chemical element, which have differing numbers of neutrons. Atoms of a particular element by definition must contain the same number of protons but may have a distinct number of neutrons which differs from atom to atom, without changing the designation...
of Helium
Helium
Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...
, with 2 proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s, 1 neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
and 2 electrons per atom. Because there is an odd number of fermions inside the atom, the atom itself is also a fermion. The electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s in a normal (non-superconducting
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
) metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
also form a Fermi liquid, as do the nucleons (protons and neutrons) in an atomic nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
.
Description
The key ideas behind Landau's theory are the notion of adiabaticity and the exclusion principleExclusion principle
The Exclusion principle is a philosophical principle that states:-In physicalism:The exclusion principle is most commonly applied when one poses this scenario; One usually considers that the desire to lift one’s arm as a mental event, and the lifting on one's arm, a physical event...
. Consider a non-interacting fermion system (a Fermi gas
Fermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
), and suppose we "turn on" the interaction slowly. Landau argued that in this situation, the ground state of the Fermi gas would adiabatically transform into the ground state of the interacting system.
By Pauli's exclusion principle, the ground state
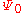of a Fermi gas consists of fermions occupying all momentum states corresponding to momentum 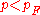with all higher momentum states unoccupied. As interaction is turned on, the spin, charge and momentum of the fermions corresponding to the occupied states remain unchanged, however, their dynamical properties, such as their mass, magnetic moment etc. are renormalizedRenormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
to new values. Thus, there is a one-to-one correspondence between the elementary excitations of a Fermi gas system and a Fermi liquid system. In the context of Fermi liquids, these excitations are called "quasi-particles".
Landau quasiparticles are long-lived excitations with a lifetime
that satifies where 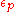is the Fermi energy.For this system, the Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
can be written (near its poles) in the form
where
is the chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
and
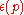is the energy corresponding to the given momentum state.The value
is called the quasiparticle residue and is very characteristic of Fermi liquid theory. The spectral function for the system can be directly observed via ARPESARPES
Angle-resolved photoemission spectroscopy , also known as ARUPS , is a direct experimental technique to observe the distribution of the electrons in the reciprocal space of solids...
experiment, and can be written (in the limit of low-lying excitations) in the form:
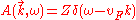
where
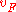is the Fermi velocity.Physically, we can say that a propagating fermion interacts with its surrounding in such a way that the net effect of the interactions is to make the fermion behave as a "dressed" fermion, altering its effective mass and other dynamical properties. These "dressed" fermions are what we think of as "quasiparticles".
Another important property of Fermi liquids is related to the scattering cross section for electrons. Suppose we have an electron with energy
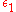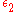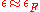above the Fermi surface, and suppose it scatters with a particle in the Fermi sea with energy . By Pauli's exclusion principle, both the particles after scattering have to lie above the Fermi surface, with energies Now, suppose the initial electron has energy very close to the Fermi surface Then, we have that also have to be very close to the Fermi surface. This reduces the phase spacePhase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
volume of the possible states after scattering, and hence, by Fermi's golden rule
Fermi's golden rule
In quantum physics, Fermi's golden rule is a way to calculate the transition rate from one energy eigenstate of a quantum system into a continuum of energy eigenstates, due to a perturbation....
, the scattering cross section goes to zero. Thus we can say that the lifetime of particles at the Fermi surface goes to infinity.
Similarities to Fermi gas
The Fermi liquid is qualitatively analogous to the non-interacting Fermi gasFermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
, in the following sense: The system's dynamics and thermodynamics at low excitation energies and temperatures may be described by substituting the interacting fermions with non-interacting quasiparticle
Quasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
s, each of which carries the same spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
and momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
as the original particles. Physically these may be thought of as being particles whose motion is disturbed by the surrounding particles and which themselves perturb the particles in their vicinity. Each many-particle excited state of the interacting system may be described by listing all occupied momentum states, just as in the non-interacting system. As a consequence, quantities such as the heat capacity of the Fermi liquid behave qualitatively in the same way as in the Fermi gas (e.g. the heat capacity rises linearly with temperature).
Energy
The energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of a many-particle state is not simply a sum of the single-particle energies of all occupied states. Instead, the change in energy for a given change
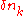in occupation of states 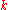contains terms both linear and quadratic in 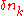(for the Fermi gas, it would only be linear, 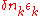, where 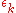denotes the single-particle energies). The linear contribution corresponds to renormalized single-particle energies, which involve, e.g., a change in the effective mass of particles. The quadratic terms correspond to a sort of "mean-field" interaction between quasiparticles, which is parameterized by so-called Landau Fermi liquid parameters and determines the behaviour of density oscillations (and spin-density oscillations) in the Fermi liquid. Still, these mean-field interactions do not lead to a scattering of quasi-particles with a transfer of particles between different momentum states.Specific heat and compressibility
Specific heat, compressibility, spin-susceptibility and other quantities show the same qualitative behaviour (e.g. dependence on temperature) as in the Fermi gas, but the magnitude is (sometimes strongly) changed.Interactions
In addition to the mean-field interactions, some weak interactions between quasiparticles remain, which lead to scattering of quasiparticles off each other. Therefore, quasiparticles acquire a finite lifetime. However, at low enough energies above the Fermi surface, this lifetime becomes very long, such that the product of excitation energy (expressed in frequency) and lifetime is much larger than one. In this sense, the quasiparticle energy is still well-defined (in the opposite limit, Heisenberg's uncertainty relationUncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
would prevent an accurate definition of the energy).
Structure
The structure of the "bare" particle's (as opposed to quasiparticle) Green's functionGreen's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
is similar to that in the Fermi gas (where, for a given momentum, the Green's function in frequency space is a delta peak at the respective single-particle energy). The delta peak in the density-of-states is broadened (with a width given by the quasiparticle lifetime). In addition (and in contrast to the quasiparticle Green's function), its weight (integral over frequency) is suppressed by a quasiparticle weight factor
. The remainder of the total weight is in a broad "incoherent background", corresponding to the strong effects of interactions on the fermions at short time-scales.Distribution
The distribution of particles (as opposed to quasiparticles) over momentum states at zero temperature still shows a discontinuous jump at the Fermi surface (as in the Fermi gas), but it does not drop from 1 to 0: the step is only of size.Resistance
In a metal the resistance at low temperatures is dominated by electron-electron scattering in combination with Umklapp scatteringUmklapp scattering
Umklapp scattering is the transformation, like a reflection or a translation, of a wave vector to another Brillouin zone as a result of a scattering process, for example an electron-lattice potential scattering or an anharmonic phonon-phonon scattering process, reflecting an electronic state or...
. For a Fermi liquid, the resistance from this mechanism varies as
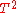, which is often taken as an experimental check for Fermi liquid behaviour (in addition to the linear temperature-dependence of the specific heat), although it only arises in combination with the lattice.Instabilities of the Fermi Liquid
The experimental observation of exotic phases in strongly correlated systems has triggered an enormous effort from the theoretical community to try to understand their microscopical origin. One possible route to detect instabilities of a FL is precisely the analysis done by Pomeranchuk. Due to that, the Pomeranchuk instability has been studied by several authors with different techniques in the last few years and in particular, the instability of the FL towards the nematic phase was investigated for several models.Non-Fermi liquids
The term non-Fermi liquid is used to describe a system which displays breakdown of Fermi-liquid behaviour. The simplest example of such a system is the system of interacting fermions in one-dimension, called Luttinger liquidLuttinger liquid
A Tomonaga-Luttinger liquid, more often referred to as simply a Luttinger liquid, is a theoretical model describing interacting electrons in a one-dimensional conductor...
. Although Luttinger liquids are physically the same as Fermi liquids, the restriction to one dimension gives rise to several qualitative differences such as the absence of a quasiparticle peak in the momentum dependent spectral function and the presence of spin density waves
Spin wave
Spin waves are propagating disturbances in the ordering of magnetic materials. These low-lying collective excitations occur in magnetic lattices with continuous symmetry. From the equivalent quasiparticle point of view, spin waves are known as magnons, which are boson modes of the spin lattice...
.
Another example of such behaviour is observed at quantum critical point
Critical point
Critical point may refer to:*Critical point *Critical point *Critical point *Construction point of a ski jumping hill-See also:*Brillouin zone*Percolation thresholds...
s of certain second-order phase transitions, such as
Heavy fermion
Heavy Fermion
In solid-state physics, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons. Electrons, a kind of fermion, found in such materials are sometimes referred to as heavy electrons...
criticality, Mott criticality
Mott insulator
Mott insulators are a class of materials that should conduct electricity under conventional band theories, but are insulators when measured...
and high-
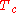cuprate phase transitions. The ground state of such transitions is characterized by the presence of a sharp Fermi surface, although there may not be well-defined quasiparticles. That is, on approaching the critical point, it is observed that the quasiparticle residue Understanding the behaviour of non-Fermi liquids is an important problem in condensed matter physics. Approaches towards explaining these phenomena include the treatment of marginal Fermi liquids; attempts to understand critical points and derive scaling relations; and descriptions using emergent gauge theories
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
with techniques of holographic
Holographic principle
The holographic principle is a property of quantum gravity and string theories which states that the description of a volume of space can be thought of as encoded on a boundary to the region—preferably a light-like boundary like a gravitational horizon...
gauge/gravity duality.
See also
- Fermi gasFermi gasA Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
- Classical fluidsClassical fluidsClassical fluids are systems of particles which retain a definite volume, and are at sufficiently high temperatures that quantum effects can be neglected. A system of hard spheres, interacting only by hard collisions , is a model classical fluid. Such a system is well described by the Percus-Yevik...
- Fermionic condensateFermionic condensateA fermionic condensate is a superfluid phase formed by fermionic particles at low temperatures. It is closely related to the Bose–Einstein condensate, a superfluid phase formed by bosonic atoms under similar conditions. Unlike the Bose–Einstein condensates, fermionic condensates are formed using...
- Luttinger liquidLuttinger liquidA Tomonaga-Luttinger liquid, more often referred to as simply a Luttinger liquid, is a theoretical model describing interacting electrons in a one-dimensional conductor...
- Luttinger's theoremLuttinger's theoremIn condensed matter physics, Luttinger's theorem is a result derived by J. M. Luttinger and J. C. Ward in 1960 that has broad implications in the field of electron transport...
- Zero soundZero soundZero sound is the name given by Landau to the unique quantum vibrations in quantum Fermi liquids.This sound can no longer be thought of as a simple wave of compression and rarefaction....