
Faraday's law of induction
Encyclopedia
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism
relating to the operating principles of transformer
s, inductor
s, and many types of electrical
motors
and generators
. Faraday's law is applicable to a closed circuit made of thin wire and states that:
Or alternatively:
The law strictly holds only when the closed circuit is an infinitely-thin wire; for example, a spinning homopolar generator
has a constant magnetically-induced EMF, but its magnetic flux does not rise perpetually higher and higher, as would be implied by a naive interpretation of the statements above.
EMF is defined as the energy available per unit charge that travels once around the wire loop (the unit of EMF is the volt
). Equivalently, it is the voltage that would be measured by cutting the wire to create an open circuit, and attaching a voltmeter
to the leads. According to the Lorentz force law, the EMF on a wire loop is:
Faraday's law of induction is closely related to the Maxwell-Faraday equation:
where: denotes curl
denotes curl
The Maxwell-Faraday equation is one of the four Maxwell's equations
, and therefore plays a fundamental role in the theory of classical electromagnetism
.
was discovered independently by Michael Faraday
and Joseph Henry
in 1831; however, Faraday was the first to publish the results of his experiments.
 In Faraday's first experimental demonstration of electromagnetic induction (August 29, 1831), he wrapped two wires around opposite sides of an iron torus (an arrangement similar to a modern transformer
In Faraday's first experimental demonstration of electromagnetic induction (August 29, 1831), he wrapped two wires around opposite sides of an iron torus (an arrangement similar to a modern transformer
). Based on his assessment of recently-discovered properties of electromagnets, he expected that when current started to flow in one wire, a sort of wave would travel through the ring and cause some electrical effect on the opposite side. He plugged one wire into a galvanometer
, and watched it as he connected the other wire to a battery. Indeed, he saw a transient current (which he called a "wave of electricity") when he connected the wire to the battery, and another when he disconnected it. This induction was due to the change in magnetic flux
that occurred when the battery was connected and disconnected. Within two months, Faraday had found several other manifestations of electromagnetic induction. For example, he saw transient currents when he quickly slid a bar magnet in and out of a coil of wires, and he generated a steady (DC
) current by rotating a copper disk near a bar magnet with a sliding electrical lead ("Faraday's disk").
Faraday explained electromagnetic induction using a concept he called lines of force. However, scientists at the time widely rejected his theoretical ideas, mainly because they were not formulated mathematically. An exception was Maxwell
, who used Faraday's ideas as the basis of his quantitative electromagnetic theory. In Maxwell's papers, the time varying aspect of electromagnetic induction is expressed as a differential equation which Oliver Heaviside
referred to as Faraday's law
even though it is slightly different in form from the original version of Faraday's law, and does not describe motional EMF. Heaviside's version (see Maxwell-Faraday equation below) is the form recognized today in the group of equations known as Maxwell's equations
.
Lenz's law, formulated by Heinrich Lenz
in 1834, describes "flux through the circuit", and gives the direction of the induced electromotive force and current resulting from electromagnetic induction (elaborated upon in the examples below).
drew attention to this fact in his 1861 paper On Physical Lines of Force. In the latter half of part II of that paper, Maxwell gives a separate physical explanation for each of the two phenomena. A reference to these two aspects of electromagnetic induction is made in some modern textbooks. As Richard Feynman states:
Reflection on this apparent dichotomy was one of the principal paths that led Einstein to develop special relativity
:
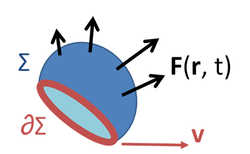
 Faraday's law of induction makes use of the magnetic flux
Faraday's law of induction makes use of the magnetic flux
ΦB through a hypothetical surface Σ whose boundary is a wire loop. Since the wire loop may be moving, we write Σ(t) for the surface. The magnetic flux is defined by a surface integral
:
where dA is an element of surface area of the moving surface Σ(t), B is the magnetic field, and B·dA is a vector dot product
. In more visual terms, the magnetic flux through the wire loop is proportional to the number of magnetic flux lines
that pass through the loop.
When the flux changes—because B changes, or because the wire loop is moved or deformed, or both—Faraday's law of induction says that the wire loop acquires an EMF
 , defined as the energy available per unit charge that travels once around the wire loop (the unit of EMF is the volt
, defined as the energy available per unit charge that travels once around the wire loop (the unit of EMF is the volt
). The EMF is given by the rate of change
of the magnetic flux:
where is the magnitude of the electromotive force
is the magnitude of the electromotive force
(EMF) in volt
s and
ΦB is the magnetic flux
in webers. The direction of the electromotive force is given by Lenz's law
.
For a tightly-wound coil of wire
, composed of N identical loops, each with the same ΦB, Faraday's law of induction states that

where N is the number of turns of wire and ΦB is the magnetic flux in webers through a single loop.
 A changing magnetic field creates an electric field; this phenomenon is described by the Maxwell-Faraday equation:
A changing magnetic field creates an electric field; this phenomenon is described by the Maxwell-Faraday equation:

where: denotes curl
denotes curl
This equation appears in modern sets of Maxwell's equations
and is often referred to as Faraday's law. It can also be written in an integral form by the Kelvin-Stokes theorem:

where, as indicated in the figure:
Both dℓ and dA have a sign ambiguity; to get the correct sign, the right-hand rule
is used, as explained in the article Kelvin-Stokes theorem. For a planar surface Σ, a positive path element dℓ of curve ∂Σ is defined by the right-hand rule as one that points with the fingers of the right hand when the thumb points in the direction of the normal n to the surface Σ.
The integral around ∂Σ is called a path integral or line integral
. The surface integral
at the right-hand side of the Maxwell-Faraday equation is the explicit expression for the magnetic flux
ΦB through Σ.
Notice that a nonzero path integral
for E is different from the behavior of the electric field generated by charges. A charge-generated E-field can be expressed as the gradient of a scalar field
that is a solution to Poisson's equation
, and has a zero path integral. See gradient theorem
.
The integral equation is true for any path ∂Σ through space, and any surface Σ for which that path is a boundary.
If the path Σ is not changing in time, the equation can be rewritten:
(including the Maxwell-Faraday equation), along with the Lorentz force law, are a sufficient foundation to derive everything in classical electromagnetism
. Therefore it is possible to "prove" Faraday's law starting with these equations. Click "show" in the box below for an outline of this proof. (In an alternative approach, not shown here but equally valid, Faraday's law could be taken as the starting point and used to "prove" the Maxwell-Faraday equation and/or other laws.)
(above left): A spinning circular metal disc in a homogeneous magnetic field generates a DC (constant in time) EMF. In Faraday's law, EMF is the time-derivative of flux, so a DC EMF is only possible if the magnetic flux is getting uniformly larger and larger perpetually. But in the generator, the magnetic field is constant and the disc stays in the same position, so no magnetic fluxes are growing larger and larger. So this example cannot be analyzed directly with Faraday's law.
Another example, due to Feynman, has a dramatic change in flux through a circuit, even though the EMF is arbitrarily small. See figure and caption above right.
In both these examples, the changes in the current path are different from the motion of the material making up the circuit. The electrons in a material tend to follow the motion of the atoms that make up the material, due to scattering
in the bulk and work function
confinement at the edges. Therefore, motional EMF is generated when a material's atoms are moving through a magnetic field, dragging the electrons with them, thus subjecting the electrons to the Lorentz force
. In the homopolar generator, the material's atoms are moving, even though the overall geometry of the circuit is staying the same. In the second example, the material's atoms are almost stationary, even though the overall geometry of the circuit is changing dramatically. On the other hand, Faraday's law always holds for thin wires, because there the geometry of the circuit always changes in a direct relationship to the motion of the material's atoms.
Although Faraday's law does not apply to all situations, the Maxwell-Faraday equation and Lorentz force law are always correct and can always be used directly.

The EMF generated by Faraday's law of induction due to relative movement of a circuit and a magnetic field is the phenomenon underlying electrical generator
s. When a permanent magnet
is moved relative to a conductor, or vice versa, an electromotive force is created. If the wire is connected through an electrical load, current will flow, and thus electrical energy is generated, converting the mechanical energy of motion to electrical energy. For example, the drum generator is based upon the figure to the right. A different implementation of this idea is the Faraday's disc
, shown in simplified form on the right.
In the Faraday's disc example, the disc is rotated in a uniform magnetic field perpendicular to the disc, causing a current to flow in the radial arm due to the Lorentz force. It is interesting to understand how it arises that mechanical work is necessary to drive this current. When the generated current flows through the conducting rim, a magnetic field is generated by this current through Ampère's circuital law (labeled "induced B" in the figure). The rim thus becomes an electromagnet
that resists rotation of the disc (an example of Lenz's law
). On the far side of the figure, the return current flows from the rotating arm through the far side of the rim to the bottom brush. The B-field induced by this return current opposes the applied B-field, tending to decrease the flux through that side of the circuit, opposing the increase in flux due to rotation. On the near side of the figure, the return current flows from the rotating arm through the near side of the rim to the bottom brush. The induced B-field increases the flux on this side of the circuit, opposing the decrease in flux due to rotation. Thus, both sides of the circuit generate an emf opposing the rotation. The energy required to keep the disc moving, despite this reactive force, is exactly equal to the electrical energy generated (plus energy wasted due to friction
, Joule heating, and other inefficiencies). This behavior is common to all generators converting mechanical energy
to electrical energy.
. In the absence of irreversible effects, like friction or Joule heating, the disc turns at the rate necessary to make d ΦB / dt equal to the voltage driving the current.

where ℓ is the distance between electrodes in the magnetic flow meter.
There are a number of methods employed to control these undesirable inductive effects.
 Eddy currents occur when a solid metallic mass is rotated in a magnetic field, because the outer portion of the metal cuts more lines of force than the inner portion, hence the induced electromotive force not being uniform, tends to set up currents between the points of greatest and least potential. Eddy currents consume a considerable amount of energy and often cause a harmful rise in temperature.
Eddy currents occur when a solid metallic mass is rotated in a magnetic field, because the outer portion of the metal cuts more lines of force than the inner portion, hence the induced electromotive force not being uniform, tends to set up currents between the points of greatest and least potential. Eddy currents consume a considerable amount of energy and often cause a harmful rise in temperature.
 Only five laminations or plates are shown in this example, so as to show the subdivision of the eddy currents. In practical use, the number of laminations or punchings ranges from 40 to 66 per inch, and brings the eddy current loss down to about one percent. While the plates can be separated by insulation, the voltage is so low that the natural rust/oxide coating of the plates is enough to prevent current flow across the laminations.
Only five laminations or plates are shown in this example, so as to show the subdivision of the eddy currents. In practical use, the number of laminations or punchings ranges from 40 to 66 per inch, and brings the eddy current loss down to about one percent. While the plates can be separated by insulation, the voltage is so low that the natural rust/oxide coating of the plates is enough to prevent current flow across the laminations.
 This is a rotor approximately 20mm in diameter from a DC motor used in a CD player. Note the laminations of the electromagnet pole pieces, used to limit parasitic inductive losses.
This is a rotor approximately 20mm in diameter from a DC motor used in a CD player. Note the laminations of the electromagnet pole pieces, used to limit parasitic inductive losses.
 In this illustration, a solid copper bar inductor on a rotating armature is just passing under the tip of the pole piece N of the field magnet. Note the uneven distribution of the lines of force across the bar inductor. The magnetic field is more concentrated and thus stronger on the left edge of the copper bar (a,b) while the field is weaker on the right edge (c,d). Since the two edges of the bar move with the same velocity, this difference in field strength across the bar creates whorls or current eddies within the copper bar.
In this illustration, a solid copper bar inductor on a rotating armature is just passing under the tip of the pole piece N of the field magnet. Note the uneven distribution of the lines of force across the bar inductor. The magnetic field is more concentrated and thus stronger on the left edge of the copper bar (a,b) while the field is weaker on the right edge (c,d). Since the two edges of the bar move with the same velocity, this difference in field strength across the bar creates whorls or current eddies within the copper bar.
This is one reason high voltage devices tend to be more efficient than low voltage devices. High voltage devices use many turns of small-gauge wire in motors, generators, and transformers. These many small turns of inductor wire in the electromagnet break up the eddy flows that can form within the large, thick inductors of low voltage, high current devices.
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
relating to the operating principles of transformer
Transformer
A transformer is a device that transfers electrical energy from one circuit to another through inductively coupled conductors—the transformer's coils. A varying current in the first or primary winding creates a varying magnetic flux in the transformer's core and thus a varying magnetic field...
s, inductor
Inductor
An inductor is a passive two-terminal electrical component used to store energy in a magnetic field. An inductor's ability to store magnetic energy is measured by its inductance, in units of henries...
s, and many types of electrical
Electricity
Electricity is a general term encompassing a variety of phenomena resulting from the presence and flow of electric charge. These include many easily recognizable phenomena, such as lightning, static electricity, and the flow of electrical current in an electrical wire...
motors
Electric motor
An electric motor converts electrical energy into mechanical energy.Most electric motors operate through the interaction of magnetic fields and current-carrying conductors to generate force...
and generators
Electrical generator
In electricity generation, an electric generator is a device that converts mechanical energy to electrical energy. A generator forces electric charge to flow through an external electrical circuit. It is analogous to a water pump, which causes water to flow...
. Faraday's law is applicable to a closed circuit made of thin wire and states that:
Or alternatively:
The law strictly holds only when the closed circuit is an infinitely-thin wire; for example, a spinning homopolar generator
Homopolar generator
A homopolar generator is a DC electrical generator comprising an electrically conductive disc rotating in a plane perpendicular to a uniform static magnetic field. A potential difference is created between the center of the disc and the rim, the electrical polarity depending on the direction of...
has a constant magnetically-induced EMF, but its magnetic flux does not rise perpetually higher and higher, as would be implied by a naive interpretation of the statements above.
EMF is defined as the energy available per unit charge that travels once around the wire loop (the unit of EMF is the volt
Volt
The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the...
). Equivalently, it is the voltage that would be measured by cutting the wire to create an open circuit, and attaching a voltmeter
Voltmeter
A voltmeter is an instrument used for measuring electrical potential difference between two points in an electric circuit. Analog voltmeters move a pointer across a scale in proportion to the voltage of the circuit; digital voltmeters give a numerical display of voltage by use of an analog to...
to the leads. According to the Lorentz force law, the EMF on a wire loop is:

Faraday's law of induction is closely related to the Maxwell-Faraday equation:

where:
 denotes curl
denotes curl
- E is the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
- B is the magnetic flux density, or magnetic field.
The Maxwell-Faraday equation is one of the four Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, and therefore plays a fundamental role in the theory of classical electromagnetism
Classical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
.
History
Electromagnetic inductionElectromagnetic induction
Electromagnetic induction is the production of an electric current across a conductor moving through a magnetic field. It underlies the operation of generators, transformers, induction motors, electric motors, synchronous motors, and solenoids....
was discovered independently by Michael Faraday
Michael Faraday
Michael Faraday, FRS was an English chemist and physicist who contributed to the fields of electromagnetism and electrochemistry....
and Joseph Henry
Joseph Henry
Joseph Henry was an American scientist who served as the first Secretary of the Smithsonian Institution, as well as a founding member of the National Institute for the Promotion of Science, a precursor of the Smithsonian Institution. During his lifetime, he was highly regarded...
in 1831; however, Faraday was the first to publish the results of his experiments.

Transformer
A transformer is a device that transfers electrical energy from one circuit to another through inductively coupled conductors—the transformer's coils. A varying current in the first or primary winding creates a varying magnetic flux in the transformer's core and thus a varying magnetic field...
). Based on his assessment of recently-discovered properties of electromagnets, he expected that when current started to flow in one wire, a sort of wave would travel through the ring and cause some electrical effect on the opposite side. He plugged one wire into a galvanometer
Galvanometer
A galvanometer is a type of ammeter: an instrument for detecting and measuring electric current. It is an analog electromechanical transducer that produces a rotary deflection of some type of pointer in response to electric current flowing through its coil in a magnetic field. .Galvanometers were...
, and watched it as he connected the other wire to a battery. Indeed, he saw a transient current (which he called a "wave of electricity") when he connected the wire to the battery, and another when he disconnected it. This induction was due to the change in magnetic flux
Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
that occurred when the battery was connected and disconnected. Within two months, Faraday had found several other manifestations of electromagnetic induction. For example, he saw transient currents when he quickly slid a bar magnet in and out of a coil of wires, and he generated a steady (DC
Direct current
Direct current is the unidirectional flow of electric charge. Direct current is produced by such sources as batteries, thermocouples, solar cells, and commutator-type electric machines of the dynamo type. Direct current may flow in a conductor such as a wire, but can also flow through...
) current by rotating a copper disk near a bar magnet with a sliding electrical lead ("Faraday's disk").
Faraday explained electromagnetic induction using a concept he called lines of force. However, scientists at the time widely rejected his theoretical ideas, mainly because they were not formulated mathematically. An exception was Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
, who used Faraday's ideas as the basis of his quantitative electromagnetic theory. In Maxwell's papers, the time varying aspect of electromagnetic induction is expressed as a differential equation which Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
referred to as Faraday's law
Faraday's law
Faraday's law may refer to the following:*Faraday's laws of electrolysis in chemistry*Faraday's law of induction, also known as Faraday-Lenz Law, in electromagnetism physics**The Maxwell–Faraday equation...
even though it is slightly different in form from the original version of Faraday's law, and does not describe motional EMF. Heaviside's version (see Maxwell-Faraday equation below) is the form recognized today in the group of equations known as Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
.
Lenz's law, formulated by Heinrich Lenz
Heinrich Lenz
Heinrich Friedrich Emil Lenz was a Russian physicist of Baltic German ethnicity. He is most noted for formulating Lenz's law in electrodynamics in 1833....
in 1834, describes "flux through the circuit", and gives the direction of the induced electromotive force and current resulting from electromagnetic induction (elaborated upon in the examples below).
Faraday's law as two different phenomena
Some physicists have remarked that Faraday's law is a single equation describing two different phenomena: the motional EMF generated by a magnetic force on a moving wire (see Lorentz force), and the transformer EMF generated by an electric force due to a changing magnetic field (due to the Maxwell-Faraday equation). James Clerk MaxwellJames Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
drew attention to this fact in his 1861 paper On Physical Lines of Force. In the latter half of part II of that paper, Maxwell gives a separate physical explanation for each of the two phenomena. A reference to these two aspects of electromagnetic induction is made in some modern textbooks. As Richard Feynman states:
Reflection on this apparent dichotomy was one of the principal paths that led Einstein to develop special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
:
Flux through a surface and EMF around a loop


Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
ΦB through a hypothetical surface Σ whose boundary is a wire loop. Since the wire loop may be moving, we write Σ(t) for the surface. The magnetic flux is defined by a surface integral
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
:
where dA is an element of surface area of the moving surface Σ(t), B is the magnetic field, and B·dA is a vector dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
. In more visual terms, the magnetic flux through the wire loop is proportional to the number of magnetic flux lines
Field line
A field line is a locus that is defined by a vector field and a starting location within the field. Field lines are useful for visualizing vector fields, which are otherwise hard to depict...
that pass through the loop.
When the flux changes—because B changes, or because the wire loop is moved or deformed, or both—Faraday's law of induction says that the wire loop acquires an EMF
Electromotive force
In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
 , defined as the energy available per unit charge that travels once around the wire loop (the unit of EMF is the volt
, defined as the energy available per unit charge that travels once around the wire loop (the unit of EMF is the voltVolt
The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the...
). The EMF is given by the rate of change
Time derivative
A time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as t\,.-Notation:...
of the magnetic flux:

where
 is the magnitude of the electromotive force
is the magnitude of the electromotive forceElectromotive force
In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
(EMF) in volt
Volt
The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the...
s and
ΦB is the magnetic flux
Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
in webers. The direction of the electromotive force is given by Lenz's law
Lenz's law
Lenz's law is a common way of understanding how electromagnetic circuits must always obey Newton's third law and The Law of Conservation of Energy...
.
For a tightly-wound coil of wire
Inductor
An inductor is a passive two-terminal electrical component used to store energy in a magnetic field. An inductor's ability to store magnetic energy is measured by its inductance, in units of henries...
, composed of N identical loops, each with the same ΦB, Faraday's law of induction states that

where N is the number of turns of wire and ΦB is the magnetic flux in webers through a single loop.
The Maxwell-Faraday equation


where:
 denotes curl
denotes curl
- E is the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
- B is the magnetic flux density.
This equation appears in modern sets of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
and is often referred to as Faraday's law. It can also be written in an integral form by the Kelvin-Stokes theorem:

where, as indicated in the figure:
- Σ is a surface bounded by the closed contour ∂Σ,
- E is the electric field,
- dℓ is an infinitesimalInfinitesimalInfinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
vector element of the contour ∂Σ, - B is the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
. - dA is an infinitesimal vector element of surface Σ. If its direction is orthogonal to that surface patch, the magnitude is the area of an infinitesimal patch of surface.
Both dℓ and dA have a sign ambiguity; to get the correct sign, the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
is used, as explained in the article Kelvin-Stokes theorem. For a planar surface Σ, a positive path element dℓ of curve ∂Σ is defined by the right-hand rule as one that points with the fingers of the right hand when the thumb points in the direction of the normal n to the surface Σ.
The integral around ∂Σ is called a path integral or line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
. The surface integral
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
at the right-hand side of the Maxwell-Faraday equation is the explicit expression for the magnetic flux
Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
ΦB through Σ.
Notice that a nonzero path integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
for E is different from the behavior of the electric field generated by charges. A charge-generated E-field can be expressed as the gradient of a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
that is a solution to Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
, and has a zero path integral. See gradient theorem
Gradient theorem
The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve: \phi\left-\phi\left = \int_L...
.
The integral equation is true for any path ∂Σ through space, and any surface Σ for which that path is a boundary.
If the path Σ is not changing in time, the equation can be rewritten:

Proof of Faraday's law
The four Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
(including the Maxwell-Faraday equation), along with the Lorentz force law, are a sufficient foundation to derive everything in classical electromagnetism
Classical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
. Therefore it is possible to "prove" Faraday's law starting with these equations. Click "show" in the box below for an outline of this proof. (In an alternative approach, not shown here but equally valid, Faraday's law could be taken as the starting point and used to "prove" the Maxwell-Faraday equation and/or other laws.)
| Outline of proof of Faraday's law from Maxwell's equations and the Lorentz force law. |
|---|
: The integral can change over time for two reasons: The integrand can change, or the integration region can change. These add linearly, therefore:  where t0 is any given fixed time. We will show that the first term on the right-hand side corresponds to transformer EMF, the second to motional EMF (see above). The first term on the right-hand side can be rewritten using the integral form of the Maxwell-Faraday equation:  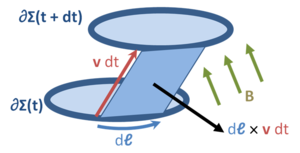  This is the most difficult part of the proof; more details and alternate approaches can be found in references. As the loop moves and/or deforms, it sweeps out a surface (see figure on right). The magnetic flux through this swept-out surface corresponds to the magnetic flux that is either entering or exiting the loop, and therefore this is the magnetic flux that contributes to the time-derivative. (This step implicitly uses Gauss's law for magnetism: Since the flux lines have no beginning or end, they can only get into the loop by getting cut through by the wire.) As a small part of the loop  moves with velocity v for a short time moves with velocity v for a short time  , it sweeps out a vector area vector , it sweeps out a vector area vector  . Therefore, the change in magnetic flux through the loop here is . Therefore, the change in magnetic flux through the loop here is Therefore:  where v is the velocity of a point on the loop  . .Putting these together,  Meanwhile, EMF is defined as the energy available per unit charge that travels once around the wire loop. Therefore, by the Lorentz force law,  Combining these,  |
"Counterexamples" to Faraday's law
Although Faraday's law is always true for loops of thin wire, it can give the wrong result if naively extrapolated to other contexts. One example is the homopolar generatorHomopolar generator
A homopolar generator is a DC electrical generator comprising an electrically conductive disc rotating in a plane perpendicular to a uniform static magnetic field. A potential difference is created between the center of the disc and the rim, the electrical polarity depending on the direction of...
(above left): A spinning circular metal disc in a homogeneous magnetic field generates a DC (constant in time) EMF. In Faraday's law, EMF is the time-derivative of flux, so a DC EMF is only possible if the magnetic flux is getting uniformly larger and larger perpetually. But in the generator, the magnetic field is constant and the disc stays in the same position, so no magnetic fluxes are growing larger and larger. So this example cannot be analyzed directly with Faraday's law.
Another example, due to Feynman, has a dramatic change in flux through a circuit, even though the EMF is arbitrarily small. See figure and caption above right.
In both these examples, the changes in the current path are different from the motion of the material making up the circuit. The electrons in a material tend to follow the motion of the atoms that make up the material, due to scattering
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
in the bulk and work function
Work function
In solid-state physics, the work function is the minimum energy needed to remove an electron from a solid to a point immediately outside the solid surface...
confinement at the edges. Therefore, motional EMF is generated when a material's atoms are moving through a magnetic field, dragging the electrons with them, thus subjecting the electrons to the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
. In the homopolar generator, the material's atoms are moving, even though the overall geometry of the circuit is staying the same. In the second example, the material's atoms are almost stationary, even though the overall geometry of the circuit is changing dramatically. On the other hand, Faraday's law always holds for thin wires, because there the geometry of the circuit always changes in a direct relationship to the motion of the material's atoms.
Although Faraday's law does not apply to all situations, the Maxwell-Faraday equation and Lorentz force law are always correct and can always be used directly.
Electrical generator

The EMF generated by Faraday's law of induction due to relative movement of a circuit and a magnetic field is the phenomenon underlying electrical generator
Electrical generator
In electricity generation, an electric generator is a device that converts mechanical energy to electrical energy. A generator forces electric charge to flow through an external electrical circuit. It is analogous to a water pump, which causes water to flow...
s. When a permanent magnet
Magnet
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, and attracts or repels other magnets.A permanent magnet is an object...
is moved relative to a conductor, or vice versa, an electromotive force is created. If the wire is connected through an electrical load, current will flow, and thus electrical energy is generated, converting the mechanical energy of motion to electrical energy. For example, the drum generator is based upon the figure to the right. A different implementation of this idea is the Faraday's disc
Homopolar generator
A homopolar generator is a DC electrical generator comprising an electrically conductive disc rotating in a plane perpendicular to a uniform static magnetic field. A potential difference is created between the center of the disc and the rim, the electrical polarity depending on the direction of...
, shown in simplified form on the right.
In the Faraday's disc example, the disc is rotated in a uniform magnetic field perpendicular to the disc, causing a current to flow in the radial arm due to the Lorentz force. It is interesting to understand how it arises that mechanical work is necessary to drive this current. When the generated current flows through the conducting rim, a magnetic field is generated by this current through Ampère's circuital law (labeled "induced B" in the figure). The rim thus becomes an electromagnet
Electromagnet
An electromagnet is a type of magnet in which the magnetic field is produced by the flow of electric current. The magnetic field disappears when the current is turned off...
that resists rotation of the disc (an example of Lenz's law
Lenz's law
Lenz's law is a common way of understanding how electromagnetic circuits must always obey Newton's third law and The Law of Conservation of Energy...
). On the far side of the figure, the return current flows from the rotating arm through the far side of the rim to the bottom brush. The B-field induced by this return current opposes the applied B-field, tending to decrease the flux through that side of the circuit, opposing the increase in flux due to rotation. On the near side of the figure, the return current flows from the rotating arm through the near side of the rim to the bottom brush. The induced B-field increases the flux on this side of the circuit, opposing the decrease in flux due to rotation. Thus, both sides of the circuit generate an emf opposing the rotation. The energy required to keep the disc moving, despite this reactive force, is exactly equal to the electrical energy generated (plus energy wasted due to friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
, Joule heating, and other inefficiencies). This behavior is common to all generators converting mechanical energy
Mechanical energy
In physics, mechanical energy is the sum of potential energy and kinetic energy present in the components of a mechanical system. It is the energy associated with the motion and position of an object. The law of conservation of energy states that in an isolated system that is only subject to...
to electrical energy.
Electrical motor
An electrical generator can be run "backwards" to become a motor. For example, with the Faraday disc, suppose a DC current is driven through the conducting radial arm by a voltage. Then by the Lorentz force law, this traveling charge experiences a force in the magnetic field B that will turn the disc in a direction given by Fleming's left hand ruleFleming's left hand rule
Fleming's left-hand rule , and Fleming's right-hand rule are a pair of visual mnemonics that is used for working out the direction of motion in an electric motor, or the direction of electric current in an electric generator...
. In the absence of irreversible effects, like friction or Joule heating, the disc turns at the rate necessary to make d ΦB / dt equal to the voltage driving the current.
Electrical transformer
The EMF predicted by Faraday's law is also responsible for electrical transformers. When the electric current in a loop of wire changes, the changing current creates a changing magnetic field. A second wire in reach of this magnetic field will experience this change in magnetic field as a change in its coupled magnetic flux, a d ΦB / d t. Therefore, an electromotive force is set up in the second loop called the induced EMF or transformer EMF. If the two ends of this loop are connected through an electrical load, current will flow.Magnetic flow meter
Faraday's law is used for measuring the flow of electrically conductive liquids and slurries. Such instruments are called magnetic flow meters. The induced voltage ℇ generated in the magnetic field B due to a conductive liquid moving at velocity v is thus given by:
where ℓ is the distance between electrodes in the magnetic flow meter.
Parasitic induction and waste heating
All metal objects moving in relation to a static magnetic field will experience inductive power flow, as do all stationary metal objects in relation to a moving magnetic field. These power flows are occasionally undesirable, resulting in flowing electric current at very low voltage and heating of the metal.There are a number of methods employed to control these undesirable inductive effects.
- Electromagnets in electric motors, generators, and transformers do not use solid metal, but instead use thin sheets of metal plate, called laminations. These thin plates reduce the parasitic eddy currents, as described below.
- Inductive coils in electronics typically use magnetic coreMagnetic coreA magnetic core is a piece of magnetic material with a high permeability used to confine and guide magnetic fields in electrical, electromechanical and magnetic devices such as electromagnets, transformers, electric motors, inductors and magnetic assemblies. It is made of ferromagnetic metal such...
s to minimize parasitic current flow. They are a mixture of metal powder plus a resin binder that can hold any shape. The binder prevents parasitic current flow through the powdered metal.
Electromagnet laminations



Parasitic induction within inductors

This is one reason high voltage devices tend to be more efficient than low voltage devices. High voltage devices use many turns of small-gauge wire in motors, generators, and transformers. These many small turns of inductor wire in the electromagnet break up the eddy flows that can form within the large, thick inductors of low voltage, high current devices.
See also
- AlternatorAlternatorAn alternator is an electromechanical device that converts mechanical energy to electrical energy in the form of alternating current.Most alternators use a rotating magnetic field but linear alternators are occasionally used...
- Crosstalk
- Faraday paradoxFaraday paradoxThe Faraday paradox is an experiment that illustrates Michael Faraday's law of electromagnetic induction. Faraday deduced this law in 1831, after inventing the first electromagnetic generator or dynamo, but was never satisfied with his own explanation of the paradox.-The equipment:The experiment...
- Moving magnet and conductor problemMoving magnet and conductor problemThe moving magnet and conductor problem is a famous thought experiment, originating in the 19th century, concerning the intersection of classical electromagnetism and special relativity. In it, the current in a conductor moving with constant velocity, v, with respect to a magnet is calculated in...
- Vector calculus
Further reading
- Maxwell, James Clerk (1881), A treatise on electricity and magnetism, Vol. II, Chapter III, §530, p. 178. Oxford, UK: Clarendon Press. ISBN 0486606376.
External links
- A simple interactive Java tutorial on electromagnetic induction National High Magnetic Field Laboratory
- R. Vega Induction: Faraday's law and Lenz's law - Highly animated lecture
- Notes from Physics and Astronomy HyperPhysics at Georgia State University
- Faraday's Law for EMC Engineers
- Tankersley and Mosca: Introducing Faraday's law


