
External (mathematics)
Encyclopedia
The term external is useful for describing certain algebraic structures. The term comes from the concept of an external binary operation which is a binary operation that draws from some external set. To be more specific, a left external binary operation on S over R is a function 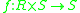 and a right external binary operation on S over R is a function
and a right external binary operation on S over R is a function 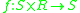 where S is the set the operation is defined on, and R is the external set (the set the operation is defined over).
where S is the set the operation is defined on, and R is the external set (the set the operation is defined over).
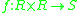 . Internal binary functions are like binary functions, but are a form of specialization, so they only accept a subset of the domains of binary functions. Here we list these terms with the function
. Internal binary functions are like binary functions, but are a form of specialization, so they only accept a subset of the domains of binary functions. Here we list these terms with the function
signatures they imply, along with some examples:
s are defined in terms of binary operations, we can define an external monoid in terms of external binary operations. For the sake of simplicity, unless otherwise specified, a left external binary operation is implied. Using the term external, we can make the generalizations:
and vector spaces are fairly straightforward, or discussed above. The only thing not covered yet is their distribution axioms. The external ring multiplication is externally distributive in
is externally distributive in 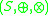 over the ring
over the ring
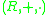 iff
iff
:
Using these terminology we can make the following local generalizations:
, and vector spaces. However, there is still no other terminology available for an external monoid for which this terminology gives us a concise expression. Above all else, this is a reason this term should be of use in the mathematical community.
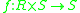 and a right external binary operation on S over R is a function
and a right external binary operation on S over R is a function 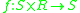 where S is the set the operation is defined on, and R is the external set (the set the operation is defined over).
where S is the set the operation is defined on, and R is the external set (the set the operation is defined over).Generalizations
The external concept is a generalization rather than a specialization, and as such, it is different from many terms in mathematics. A similar but opposite concept is that of an internal binary function from R to S, defined as a function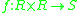 . Internal binary functions are like binary functions, but are a form of specialization, so they only accept a subset of the domains of binary functions. Here we list these terms with the function
. Internal binary functions are like binary functions, but are a form of specialization, so they only accept a subset of the domains of binary functions. Here we list these terms with the functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
signatures they imply, along with some examples:
-
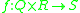 (binary functionBinary functionIn mathematics, a binary function, or function of two variables, is a function which takes two inputs.Precisely stated, a function f is binary if there exists sets X, Y, Z such that\,f \colon X \times Y \rightarrow Z...
(binary functionBinary functionIn mathematics, a binary function, or function of two variables, is a function which takes two inputs.Precisely stated, a function f is binary if there exists sets X, Y, Z such that\,f \colon X \times Y \rightarrow Z...
)- Example: exponentiationExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
(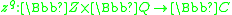 as in
as in 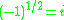 ),
), - Example: set membership (
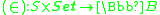 where
where 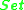 is the category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
is the category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
) - Examples: matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, the tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
, and the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
- Example: exponentiation
-
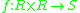 (internal binary function)
(internal binary function)
- Example: internal binary relations (
 )
) - Examples: the dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, the inner productInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, and metricsMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
.
- Example: internal binary relations (
-
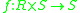 (external binary operation)
(external binary operation)
- Examples: dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
flowsFlow (mathematics)In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
, group actionsGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
, projection maps, and scalar multiplicationScalar multiplicationIn mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
.
- Examples: dynamical system
-
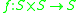 (binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
(binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
).- Examples: additionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, multiplicationMultiplicationMultiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, permutationsPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
, and the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
.
- Examples: addition
External monoids
Since monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s are defined in terms of binary operations, we can define an external monoid in terms of external binary operations. For the sake of simplicity, unless otherwise specified, a left external binary operation is implied. Using the term external, we can make the generalizations:
- An external magma
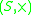 over R is a set S with an external binary operation. This satisfies
over R is a set S with an external binary operation. This satisfies 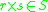 for all
for all 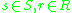 (external closureClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
(external closureClosure (mathematics)In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
). - An external semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
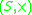 over
over 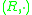 is an external magma that satisfies
is an external magma that satisfies 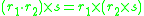 for all
for all 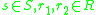 (externally associative).
(externally associative). - An external monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
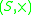 over
over 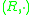 is an external semigroup in which there exists
is an external semigroup in which there exists 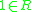 such that
such that 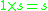 for all
for all 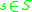 (has external identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
(has external identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
).
Modules as external rings
Much of the machinery of modulesModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
and vector spaces are fairly straightforward, or discussed above. The only thing not covered yet is their distribution axioms. The external ring multiplication
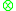 is externally distributive in
is externally distributive in 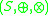 over the ring
over the ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
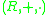 iff
iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
:
-
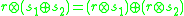 for all
for all 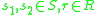 and:
and: -
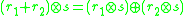 for all
for all 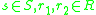
Using these terminology we can make the following local generalizations:
- An external semiring
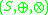 over the semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
over the semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
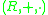 is a commutative monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
is a commutative monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
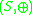 and an external monoid
and an external monoid 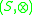 where
where 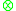 is externally distributive in
is externally distributive in 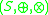 over the semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
over the semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
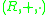 .
. - An external ring
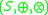 over the ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
over the ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
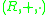 is an Abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
is an Abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
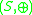 and an external monoid
and an external monoid 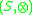 where
where 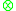 is externally distributive in
is externally distributive in 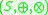 over the ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
over the ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
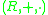 .
.
Other examples
Now that we have all the terminology we need, we can make simple connections between various structures:- Complex exponentiation forms an external monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
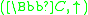 over the Abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
over the Abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
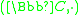 .
. - Prime factorization forests form an external semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
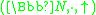 over the semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
over the semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
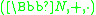 .
. - A dynamical systemDynamical system (definition)The dynamical system concept is a mathematical formalization for any fixed "rule" which describes the time dependence of a point's position in its ambient space...
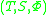 is an external monoid
is an external monoid 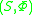 over the monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
over the monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
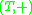 .
. - A semimodule is an external semiring over a semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
. - A moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
is an external ring over a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. - A vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
is an external ring over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
Usefulness
It could be argued that we already have terms for the concepts described here, like dynamical systems, group actions, modulesModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, and vector spaces. However, there is still no other terminology available for an external monoid for which this terminology gives us a concise expression. Above all else, this is a reason this term should be of use in the mathematical community.

