Examples of groups
Encyclopedia
Some elementary examples of groups in mathematics
are given on Group (mathematics)
.
Further examples are listed here.
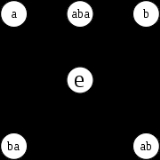
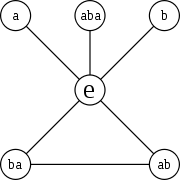Consider three colored blocks (red, green, and blue), initially placed in the order RGB. Let a be the operation "swap the first block and the second block", and b be the operation "swap the second block and the third block".
We can write xy for the operation "first do y, then do x"; so that ab is the operation RGB → RBG → BRG, which could be described as "move the first two blocks one position to the right and put the third block into the first position". If we write e for "leave the blocks as they are" (the identity operation), then we can write the six permutations of the three blocks as follows:
Note that aa has the effect RGB → GRB → RGB; so we can write aa = e. Similarly, bb = (aba)(aba) = e; (ab)(ba) = (ba)(ab) = e; so every element has an inverse.
By inspection, we can determine associativity and closure; note in particular that (ba)b = aba = b(ab).
Since it is built up from the basic operations a and b, we say that the set {a,b} generates
this group. The group, called the symmetric group
S3, has order 6, and is non-abelian (since, for example, ab ≠ ba).
For instance "move in the North-East direction for 2 miles" is a translation of the plane.
If you have two such translations a and b, they can be composed to form a new translation a ∘ b as follows: first follow the prescription of b, then that of a.
For instance, if
and
then
(see Pythagorean theorem
for why this is so, geometrically).
The set of all translations of the plane with composition as operation forms a group:
This is an Abelian group and our first (nondiscrete) example of a Lie group
: a group which is also a manifold
.
The symmetry group
Groups are very important to describe the symmetry
of objects, be they geometrical (like a tetrahedron
) or algebraic (like a set of equations).
As an example, we consider a glass square of a certain thickness (with a letter "F" written on it, just to make the different positions discriminable).
In order to describe its symmetry, we form the set of all those rigid movements of the square that don't make a visible difference (except the "F").
For instance, if you turn it by 90° clockwise, then it still looks the same, so this movement is one element of our set, let's call it a.
We could also flip it horizontally so that its underside become up.
Again, after performing this movement, the glass square looks the same, so this is also an element of our set and we call it b.
Then there's of course the movement that does nothing; it's denoted by e.
Now if you have two such movements x and y, you can define the composition x ∘ y as above: you first perform the movement y and then the movement x.
The result will leave the slab looking like before.
The point is that the set of all those movements, with composition as operation, forms a group.
This group is the most concise description of the square's symmetry.
Chemists use symmetry groups of this type to describe the symmetry of crystals.
Let's investigate our squares symmetry group some more.
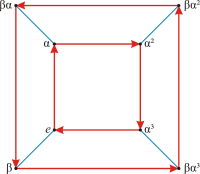
Right now, we have the elements a, b and e, but we can easily form more:
for instance a ∘ a, also written as a2, is a 180° degree turn.
a3 is a 270° clockwise rotation (or a 90° counter-clockwise rotation).
We also see that b2 = e and also a4 = e.
Here's an interesting one: what does a ∘ b do?
First flip horizontally, then rotate.
Try to visualize that a ∘ b = b ∘ a3.
Also, a2 ∘ b is a vertical flip and is equal to b ∘ a2.
This group of order 8 has the following Cayley table
:
For any two elements in the group, the table records what their composition is.
Here we wrote "a3b" as a short hand for a3 ∘ b.
Mathematicians know this group as the dihedral group
of order 8, and call it either Dih4, D4 or D8 depending on what notation they use for dihedral groups.
This was an example of a non-abelian group: the operation ∘ here is not commutative, which you can see from the table; the table is not symmetrical about the main diagonal.
The dihedral group of order 8 is isomorphic to the permutation group generated by (1234) and (13).
over the reals
, say.
This is a group with matrix multiplication as operation. It is called the general linear group
, GL(n).
Geometrically, it contains all combinations of rotations, reflections, dilations and skew transformations of n-dimensional Euclidean space
that fix
a given point (the origin).
If we restrict ourselves to matrices with determinant
1, then we get another group, the special linear group
, SL(n).
Geometrically, this consists of all the elements of GL(n) that preserve both orientation and volume of the various geometric solids in Euclidean space.
If instead we restrict ourselves to orthogonal
matrices, then we get the orthogonal group
O(n).
Geometrically, this consists of all combinations of rotations and reflections that fix the origin.
These are precisely the transformations which preserve lengths and angles.
Finally, if we impose both restrictions, then we get the special orthogonal group SO(n), which consists of rotations only.
These groups are our first examples of infinite non-abelian groups. They are also happen to be Lie group
s. In fact, most of the important Lie groups (but not all) can be expressed as matrix groups.
If this idea is generalised to matrices with complex number
s as entries, then we get further useful Lie groups, such as the unitary group
U(n).
We can also consider matrices with quaternion
s as entries; in this case, there is no well-defined notion of a determinant (and thus no good way to define a quaternionic "volume"), but we can still define a group analogous to the orthogonal group, the symplectic group
Sp(n).
Furthermore, the idea can be treated purely algebraically with matrices over any field, but then the groups are not Lie groups.
For example, we have the general linear group
s over finite field
s. The group theorist J. L. Alperin has written that "The typical example of a finite group is GL(n,q), the general linear group of n dimensions over the field with q elements. The student who is introduced to the subject with other examples is being completely misled." (Bulletin (New Series) of the American Mathematical Society, 10 (1984) 121)
with two generators a and b consists of all finite string
s that can be formed from the four symbols a, a-1, b and b-1 such that no a appears directly next to an a-1 and no b appears directly next to an b-1.
Two such strings can be concatenated and converted into a string of this type by repeatedly replacing the "forbidden" substrings with the empty string.
For instance: "abab-1a-1" concatenated with
"abab-1a" yields "abab-1a-1abab-1a", which gets reduced to "abaab-1a".
One can check that the set of those strings with this operation forms a group with neutral element the empty string ε := "".
(Usually the quotation marks are left off, which is why you need the symbol ε!)
This is another infinite non-abelian group.
Free groups are important in algebraic topology
; the free group in two generators is also used for a proof of the Banach–Tarski paradox
.
The set of maps M(S, G) is itself a group; namely for two maps f,g of S into G we define fg to be the map such that (fg)(x) = f(x)g(x) for every x∈S and f−1 to be the map such that f−1(x) = f(x)−1.
Take maps f, g, and h in M(S,G).
For every x in S, f(x) and g(x) are both in G, and so is (fg)(x).
Therefore fg is also in M(S, G), or M(S, G) is closed.
For ((fg)h)(x) = (fg)(x)h(x) = (f(x)g(x))h(x) = f(x)(g(x)h(x)) = f(x)(gh)(x) = (f(gh))(x),
M(S, G) is associative.
And there is a map i such that i(x) = e where e is the unit element of G.
The map i makes all the functions f in M(S, G) such that
if = fi = f, or i is the unit element of M(S, G).
Thus, M(S, G) is actually a group.
If G is commutative, then (fg)(x) = f(x)g(x) = g(x)f(x) = (gf)(x).
Therefore so is M(S, G).
Then G, also denoted by Perm(S) or Sym(S), is a group with ordinary composition of mappings.
The unit element of G is the identity map of S.
For two maps f and g in G are bijective, fg is also bijective.
Therefore G is closed.
The composition of maps is associative; hence G is a group.
S may be either finite, or infinite.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
are given on Group (mathematics)
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
Further examples are listed here.
Permutations of a set of three elements
We can write xy for the operation "first do y, then do x"; so that ab is the operation RGB → RBG → BRG, which could be described as "move the first two blocks one position to the right and put the third block into the first position". If we write e for "leave the blocks as they are" (the identity operation), then we can write the six permutations of the three blocks as follows:
- e : RGB → RGB
- a : RGB → GRB
- b : RGB → RBG
- ab : RGB → BRG
- ba : RGB → GBR
- aba : RGB → BGR
Note that aa has the effect RGB → GRB → RGB; so we can write aa = e. Similarly, bb = (aba)(aba) = e; (ab)(ba) = (ba)(ab) = e; so every element has an inverse.
By inspection, we can determine associativity and closure; note in particular that (ba)b = aba = b(ab).
Since it is built up from the basic operations a and b, we say that the set {a,b} generates
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
this group. The group, called the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S3, has order 6, and is non-abelian (since, for example, ab ≠ ba).
The group of translations of the plane
A translation of the plane is a rigid movement of every point of the plane for a certain distance in a certain direction.For instance "move in the North-East direction for 2 miles" is a translation of the plane.
If you have two such translations a and b, they can be composed to form a new translation a ∘ b as follows: first follow the prescription of b, then that of a.
For instance, if
- a = "move North-East for 3 miles"
and
- b = "move South-East for 4 miles"
then
- a ∘ b = "move East for 5 miles"
(see Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
for why this is so, geometrically).
The set of all translations of the plane with composition as operation forms a group:
- If a and b are translations, then a ∘ b is also a translation.
- Composition of translations is associative: (a ∘ b) ∘ c = a ∘ (b ∘ c).
- The identity element for this group is the translation with prescription "move zero miles in whatever direction you like".
- The inverse of a translation is given by walking in the opposite direction for the same distance.
This is an Abelian group and our first (nondiscrete) example of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
: a group which is also a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.
The symmetry groupSymmetry groupThe symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of a square - dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of order 8
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of objects, be they geometrical (like a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
) or algebraic (like a set of equations).
As an example, we consider a glass square of a certain thickness (with a letter "F" written on it, just to make the different positions discriminable).
In order to describe its symmetry, we form the set of all those rigid movements of the square that don't make a visible difference (except the "F").
For instance, if you turn it by 90° clockwise, then it still looks the same, so this movement is one element of our set, let's call it a.
We could also flip it horizontally so that its underside become up.
Again, after performing this movement, the glass square looks the same, so this is also an element of our set and we call it b.
Then there's of course the movement that does nothing; it's denoted by e.
Now if you have two such movements x and y, you can define the composition x ∘ y as above: you first perform the movement y and then the movement x.
The result will leave the slab looking like before.
The point is that the set of all those movements, with composition as operation, forms a group.
This group is the most concise description of the square's symmetry.
Chemists use symmetry groups of this type to describe the symmetry of crystals.
Let's investigate our squares symmetry group some more.
Right now, we have the elements a, b and e, but we can easily form more:
for instance a ∘ a, also written as a2, is a 180° degree turn.
a3 is a 270° clockwise rotation (or a 90° counter-clockwise rotation).
We also see that b2 = e and also a4 = e.
Here's an interesting one: what does a ∘ b do?
First flip horizontally, then rotate.
Try to visualize that a ∘ b = b ∘ a3.
Also, a2 ∘ b is a vertical flip and is equal to b ∘ a2.
This group of order 8 has the following Cayley table
Cayley table
A Cayley table, after the 19th century British mathematician Arthur Cayley, describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table...
:
| o | e | b | a | a2 | a3 | ab | a2b | a3b |
|---|---|---|---|---|---|---|---|---|
| e | e | b | a | a2 | a3 | ab | a2b | a3b |
| b | b | e | a3b | a2b | ab | a3 | a2 | a |
| a | a | ab | a2 | a3 | e | a2b | a3b | b |
| a2 | a2 | a2b | a3 | e | a | a3b | b | ab |
| a3 | a3 | a3b | e | a | a2 | b | ab | a2b |
| ab | ab | a | b | a3b | a2b | e | a3 | a2 |
| a2b | a2b | a2 | ab | b | a3b | a | e | a3 |
| a3b | a3b | a3 | a2b | ab | b | a2 | a | e |
For any two elements in the group, the table records what their composition is.
Here we wrote "a3b" as a short hand for a3 ∘ b.
Mathematicians know this group as the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of order 8, and call it either Dih4, D4 or D8 depending on what notation they use for dihedral groups.
This was an example of a non-abelian group: the operation ∘ here is not commutative, which you can see from the table; the table is not symmetrical about the main diagonal.
The dihedral group of order 8 is isomorphic to the permutation group generated by (1234) and (13).
Matrix groups
If n is some positive integer, we can consider the set of all invertible n by n matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
over the reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, say.
This is a group with matrix multiplication as operation. It is called the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
, GL(n).
Geometrically, it contains all combinations of rotations, reflections, dilations and skew transformations of n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
that fix
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
a given point (the origin).
If we restrict ourselves to matrices with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1, then we get another group, the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
, SL(n).
Geometrically, this consists of all the elements of GL(n) that preserve both orientation and volume of the various geometric solids in Euclidean space.
If instead we restrict ourselves to orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
matrices, then we get the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n).
Geometrically, this consists of all combinations of rotations and reflections that fix the origin.
These are precisely the transformations which preserve lengths and angles.
Finally, if we impose both restrictions, then we get the special orthogonal group SO(n), which consists of rotations only.
These groups are our first examples of infinite non-abelian groups. They are also happen to be Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s. In fact, most of the important Lie groups (but not all) can be expressed as matrix groups.
If this idea is generalised to matrices with complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s as entries, then we get further useful Lie groups, such as the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n).
We can also consider matrices with quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s as entries; in this case, there is no well-defined notion of a determinant (and thus no good way to define a quaternionic "volume"), but we can still define a group analogous to the orthogonal group, the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
Sp(n).
Furthermore, the idea can be treated purely algebraically with matrices over any field, but then the groups are not Lie groups.
For example, we have the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
s over finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s. The group theorist J. L. Alperin has written that "The typical example of a finite group is GL(n,q), the general linear group of n dimensions over the field with q elements. The student who is introduced to the subject with other examples is being completely misled." (Bulletin (New Series) of the American Mathematical Society, 10 (1984) 121)
Free group on two generators
The free groupFree group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
with two generators a and b consists of all finite string
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
s that can be formed from the four symbols a, a-1, b and b-1 such that no a appears directly next to an a-1 and no b appears directly next to an b-1.
Two such strings can be concatenated and converted into a string of this type by repeatedly replacing the "forbidden" substrings with the empty string.
For instance: "abab-1a-1" concatenated with
"abab-1a" yields "abab-1a-1abab-1a", which gets reduced to "abaab-1a".
One can check that the set of those strings with this operation forms a group with neutral element the empty string ε := "".
(Usually the quotation marks are left off, which is why you need the symbol ε!)
This is another infinite non-abelian group.
Free groups are important in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
; the free group in two generators is also used for a proof of the Banach–Tarski paradox
Banach–Tarski paradox
The Banach–Tarski paradox is a theorem in set theoretic geometry which states the following: Given a solid ball in 3-dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces , which can then be put back together in a different way to yield two...
.
The sets of maps from a set to a group
Let G be a group and S a nonempty set.The set of maps M(S, G) is itself a group; namely for two maps f,g of S into G we define fg to be the map such that (fg)(x) = f(x)g(x) for every x∈S and f−1 to be the map such that f−1(x) = f(x)−1.
Take maps f, g, and h in M(S,G).
For every x in S, f(x) and g(x) are both in G, and so is (fg)(x).
Therefore fg is also in M(S, G), or M(S, G) is closed.
For ((fg)h)(x) = (fg)(x)h(x) = (f(x)g(x))h(x) = f(x)(g(x)h(x)) = f(x)(gh)(x) = (f(gh))(x),
M(S, G) is associative.
And there is a map i such that i(x) = e where e is the unit element of G.
The map i makes all the functions f in M(S, G) such that
if = fi = f, or i is the unit element of M(S, G).
Thus, M(S, G) is actually a group.
If G is commutative, then (fg)(x) = f(x)g(x) = g(x)f(x) = (gf)(x).
Therefore so is M(S, G).
The groups of permutations
Let G be the set of bijective mappings of a set S onto itself.Then G, also denoted by Perm(S) or Sym(S), is a group with ordinary composition of mappings.
The unit element of G is the identity map of S.
For two maps f and g in G are bijective, fg is also bijective.
Therefore G is closed.
The composition of maps is associative; hence G is a group.
S may be either finite, or infinite.
Some more finite groups
- list of small groups
- List of the 230 crystallographic 3D space groups