Q-function
Encyclopedia
In statistics
, the Q-function is the tail probability of the standard normal distribution. In other words,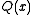
is the probability that a standard normal random variable will obtain a value larger than 
. Other definitions of the Q-function, all of which are simple transformations of the normal cumulative distribution function
, are also used occasionally.
Because of its relation to the cumulative distribution function
of the normal distribution, the Q-function can also be expressed in terms of the error function
, which is an important function in applied mathematics and physics.
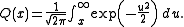
Thus,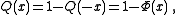
where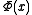
is the cumulative distribution function of the normal Gaussian distribution.
The Q-function can be expressed in terms of the error function
, or the compelementary error function, as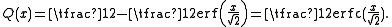
An alternative form of the Q-function that is more useful is expressed as:
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Q-function is the tail probability of the standard normal distribution. In other words,
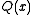is the probability that a standard normal random variable will obtain a value larger than . Other definitions of the Q-function, all of which are simple transformations of the normal cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
, are also used occasionally.
Because of its relation to the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the normal distribution, the Q-function can also be expressed in terms of the error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
, which is an important function in applied mathematics and physics.
Definition and basic properties
Formally, the Q-function is defined as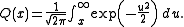Thus,
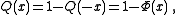
where
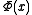is the cumulative distribution function of the normal Gaussian distribution.The Q-function can be expressed in terms of the error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
, or the compelementary error function, as
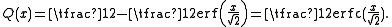
An alternative form of the Q-function that is more useful is expressed as:
Bounds
- The Q-function is not an elementary function. However, the bounds
become increasingly tight for large x, and are often useful.
Using the substitutionIntegration by substitutionIn calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
and defining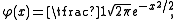 
the upper bound is derived as follows:
Similarly, using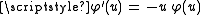
and the quotient rule,
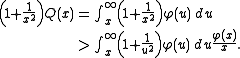
Solving for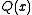
provides the lower bound.
- Chernoff boundChernoff boundIn probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
of Q-function is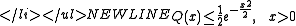
Values
The Q-function is well tabulated and can be computed directly in most of the mathematical software packages such as Matlab and Mathematica. Some values of the Q-function are given below for reference.
Q(0.0) = 0.500000000
Q(0.1) = 0.460172163
Q(0.2) = 0.420740291
Q(0.3) = 0.382088578
Q(0.4) = 0.344578258
Q(0.5) = 0.308537539
Q(0.6) = 0.274253118
Q(0.7) = 0.241963652
Q(0.8) = 0.211855399
Q(0.9) = 0.184060125
Q(1.0) = 0.158655254
Q(1.1) = 0.135666061
Q(1.2) = 0.115069670
Q(1.3) = 0.096800485
Q(1.4) = 0.080756659
Q(1.5) = 0.066807201
Q(1.6) = 0.054799292
Q(1.7) = 0.044565463
Q(1.8) = 0.035930319
Q(1.9) = 0.028716560
Q(2.0) = 0.022750132
Q(2.1) = 0.017864421
Q(2.2) = 0.013903448
Q(2.3) = 0.010724110
Q(2.4) = 0.008197536
Q(2.5) = 0.006209665
Q(2.6) = 0.004661188
Q(2.7) = 0.003466974
Q(2.8) = 0.002555130
Q(2.9) = 0.001865813
Q(3.0) = 0.001349898
Q(3.1) = 0.000967603
Q(3.2) = 0.000687138
Q(3.3) = 0.000483424
Q(3.4) = 0.000336929
Q(3.5) = 0.000232629
Q(3.6) = 0.000159109
Q(3.7) = 0.000107800
Q(3.8) = 0.000072348
Q(3.9) = 0.000048096
Q(4.0) = 0.000031671
- Chernoff bound