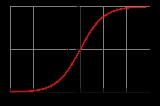
Sigmoid function
Overview
Learning curve
A learning curve is a graphical representation of the changing rate of learning for a given activity or tool. Typically, the increase in retention of information is sharpest after the initial attempts, and then gradually evens out, meaning that less and less new information is retained after each...
s, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
having an "S" shape. Often, sigmoid function refers to the special case of the logistic function
Logistic function
A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
shown at right and defined by the formula
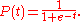
Another example is the Gompertz curve
Gompertz curve
A Gompertz curve or Gompertz function, named after Benjamin Gompertz, is a sigmoid function. It is a type of mathematical model for a time series, where growth is slowest at the start and end of a time period...
.
Unanswered Questions

