
Philo line
Encyclopedia
In geometry
, the Philo line is a line segment
defined from an angle
and a point
. The Philo line for a point P that lies inside an angle with edges d and e is the shortest line segment that passes through P and has its endpoints on d and e. Also known as the Philon line, it is named after Philo of Byzantium
, a Greek writer on mechanical devices, who lived probably during the 1st or 2nd century BC. The Philo line is not, in general, constructible
by compass and straightedge
.
, that is, to construct a geometric representation of the cube root of two, and this was Philo's purpose in defining this line (Coxeter and van de Craats, 1993). Specifically, let PQRS be a rectangle in which the aspect ratio
PQ:QR is 1:2, as in the figure below. Let TU be the Philo line of point P with respect to right angle QRS. Define point V to be the point of intersection of line TU and of the circle through points PQRS, and let W be the point where line QR crosses a perpendicular line through V. Then segments RS and RW are in proportion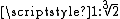 .
.
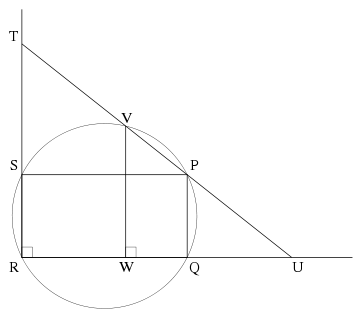
In this figure, segments PU and VT are of equal length, and RV is perpendicular to TU. These properties can be used as part of an equivalent alternative definition for the Philo line for a point P and angle edges d and e: it is a line segment connecting d to e through P such that the distance along the segment from P to d is equal to the distance along the segment from V to e, where V is the closest point on the segment to the corner point of the angle.
Since doubling the cube is impossible with compass and straightedge
, it is similarly impossible to construct the Philo line with these tools.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Philo line is a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
defined from an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
and a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
. The Philo line for a point P that lies inside an angle with edges d and e is the shortest line segment that passes through P and has its endpoints on d and e. Also known as the Philon line, it is named after Philo of Byzantium
Philo of Byzantium
Philo of Byzantium , also known as Philo Mechanicus, was a Greek engineer and writer on mechanics, who lived during the latter half of the 3rd century BC...
, a Greek writer on mechanical devices, who lived probably during the 1st or 2nd century BC. The Philo line is not, in general, constructible
Constructible number
A point in the Euclidean plane is a constructible point if, given a fixed coordinate system , the point can be constructed with unruled straightedge and compass...
by compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
.
Doubling the cube
Philo's line can be used to double the cubeDoubling the cube
Doubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction...
, that is, to construct a geometric representation of the cube root of two, and this was Philo's purpose in defining this line (Coxeter and van de Craats, 1993). Specifically, let PQRS be a rectangle in which the aspect ratio
Aspect ratio
The aspect ratio of a shape is the ratio of its longer dimension to its shorter dimension. It may be applied to two characteristic dimensions of a three-dimensional shape, such as the ratio of the longest and shortest axis, or for symmetrical objects that are described by just two measurements,...
PQ:QR is 1:2, as in the figure below. Let TU be the Philo line of point P with respect to right angle QRS. Define point V to be the point of intersection of line TU and of the circle through points PQRS, and let W be the point where line QR crosses a perpendicular line through V. Then segments RS and RW are in proportion
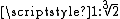 .
.
In this figure, segments PU and VT are of equal length, and RV is perpendicular to TU. These properties can be used as part of an equivalent alternative definition for the Philo line for a point P and angle edges d and e: it is a line segment connecting d to e through P such that the distance along the segment from P to d is equal to the distance along the segment from V to e, where V is the closest point on the segment to the corner point of the angle.
Since doubling the cube is impossible with compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
, it is similarly impossible to construct the Philo line with these tools.

