A conchoid is a curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

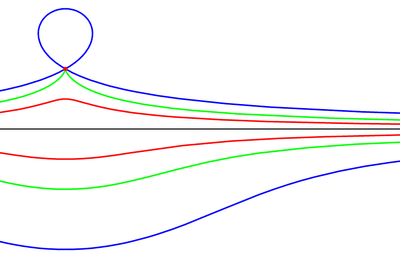
 derived from a fixed point O, another curve, and a length d. For every line through O that intersects the given curve at A the two points on the line which are d from A are on the conchoid. The conchoid is, therefore, the cissoid

Cissoid

In geometry, a cissoid is a curve generated from two given curves C1, C2 and a point O . Let L be a variable line passing through O and intersecting C1 at P1 and C2 at P2. Let P be the point on L so that OP = P1P2...

 of a circle with center O and the given curve. They are called conchoids because the shape of their outer branches resembles conch shells

Mussel

The common name mussel is used for members of several families of clams or bivalvia mollusca, from saltwater and freshwater habitats. These groups have in common a shell whose outline is elongated and asymmetrical compared with other edible clams, which are often more or less rounded or oval.The...

.

The simplest expression uses polar coordinates with O at the origin. If 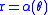expresses the given curve then r = α(θ) ± d expresses the conchoid. Parametrically, it can be expressed as x = a + cos(θ) and y = atan(θ) + sin(θ).

All conchoids are cissoids with a circle centered on O as one of the curves.

The prototype of this class is the conchoid of Nicomedes

Nicomedes (mathematician)

Nicomedes was an ancient Greek mathematician.- Life and work :Almost nothing is known about his life apart from references in his works. We know that he lived around the time of Eratosthenes or after, because he criticized Eratosthenes' method of doubling the cube...

 in which the given curve is a line

Line (mathematics)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

.

A limaçon

Limaçon

In geometry, a limaçon or limacon , also known as a limaçon of Pascal, is defined as a roulette formed when a circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller...

 is a conchoid with a circle as the given curve.

The often-so-called conchoid of de Sluze

Conchoid of de Sluze

The conchoid of de Sluze is a family of plane curves studied in 1662 by René François Walter, baron de Sluze.The curves are defined by the polar equationr=\sec\theta+a\cos\theta \,....

 and conchoid of Dürer

Conchoid of Dürer

The conchoid of Dürer, also called Dürer's shell curve, is a variant of a conchoid or plane algebraic curve. It is not a true conchoid.-Construction:...

do not fit this definition; the former is a strict cissoid and the latter a construction more general yet.