
Dimension theorem for vector spaces
Encyclopedia
In mathematics
, the dimension theorem for vector spaces states that all bases
of a vector space
have equally many elements. This number of elements may be finite, or given by an infinite cardinal number
, and defines the dimension
of the space.
Formally, the dimension theorem for vector spaces states that
If V is finitely generated, then it has a finite basis, and the result says that any two bases have the same number of elements.
While the proof of the existence of a basis for any vector space in the general case requires Zorn's lemma
and is in fact equivalent to the axiom of choice, the uniqueness of the cardinality of the basis requires only the ultrafilter lemma , which is strictly weaker (the proof given below, however, assumes trichotomy, i.e., that all cardinal number
s are comparable, a statement which is also equivalent to the axiom of choice). The theorem can be generalized to arbitrary R-modules
for rings R having invariant basis number
.
The theorem for finitely generated case can be proved with elementary arguments of linear algebra
, and requires no forms of the axiom of choice.
{ bj: j ∈ J } are both bases, with the cardinality of I bigger than the cardinality of J. From this assumption we will derive a contradiction.
Every bj can be written as a finite sum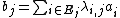 , where
, where 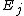 is a finite subset of
is a finite subset of 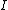 .
.
Since the cardinality of I is greater than that of J and the Ej's are finite subsets of I, the cardinality of I is also bigger than the cardinality of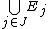 . (Note that this argument works only for infinite I.) So there is some
. (Note that this argument works only for infinite I.) So there is some 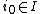 which does not appear
which does not appear
in any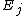 . The corresponding
. The corresponding 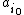 can be expressed as a finite linear combination of
can be expressed as a finite linear combination of 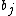 's, which in turn can be expressed as finite linear combination of
's, which in turn can be expressed as finite linear combination of 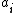 's, not involving
's, not involving  . Hence
. Hence 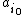 is linearly dependent on the other
is linearly dependent on the other 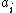 's.
's.
Every ai can be written as a sum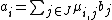
The matrix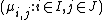 has n columns (the j-th column is the
has n columns (the j-th column is the
m-tuple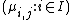 ), so it has rank at most n. This means that its m rows cannot be linearly independent. Write
), so it has rank at most n. This means that its m rows cannot be linearly independent. Write 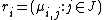 for the i-th row, then there is a nontrivial
for the i-th row, then there is a nontrivial
linear combination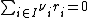
But then also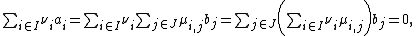
so the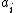 are linearly dependent.
are linearly dependent.
Theorem 1: If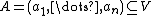 is a linearly independent tuple
is a linearly independent tuple
in a vector space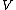 , and
, and 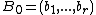 is a tuple that spans
is a tuple that spans 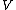 , then
, then 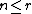 . The argument is as follows:
. The argument is as follows:
Since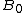 spans
spans 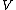 , the tuple
, the tuple 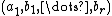 also spans. Since
also spans. Since 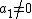 (because
(because 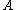 is linearly independent), there is at least one
is linearly independent), there is at least one 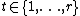 such that
such that 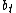 can be written as a linear combination of
can be written as a linear combination of 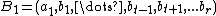 . Thus,
. Thus, 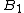 is a spanning tuple, and its length is the same as
is a spanning tuple, and its length is the same as 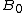 's.
's.
Repeat this process. Because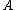 is linearly independent, we can always remove an element from the list
is linearly independent, we can always remove an element from the list 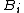 which is not one of the
which is not one of the 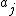 's that we prepended to the list in a prior step (because
's that we prepended to the list in a prior step (because 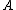 is linearly independent, and so there must be some nonzero coefficient in front of one of the
is linearly independent, and so there must be some nonzero coefficient in front of one of the 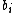 's). Thus, after
's). Thus, after  iterations, the result will be a tuple
iterations, the result will be a tuple 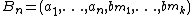 (possibly with
(possibly with 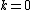 ) of length
) of length  . In particular,
. In particular, 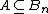 , so
, so 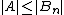 , i.e.,
, i.e., 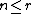 .
.
To prove the finite case of the dimension theorem from this, suppose that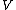 is a vector space and
is a vector space and 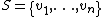 and
and 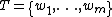 are both bases of
are both bases of 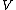 . Since
. Since 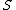 is linearly independent and
is linearly independent and 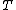 spans, we can apply Theorem 1 to get
spans, we can apply Theorem 1 to get  . And since
. And since 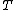 is linearly independent and
is linearly independent and 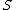 spans, we get
spans, we get 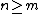 . From these, we get
. From these, we get  .
.
be a linear transformation
. Then
that is, the dimension of U is equal to the dimension of the transformation's range
plus the dimension of the kernel
. See rank-nullity theorem
for a fuller discussion.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the dimension theorem for vector spaces states that all bases
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
have equally many elements. This number of elements may be finite, or given by an infinite cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
, and defines the dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of the space.
Formally, the dimension theorem for vector spaces states that
- Given a vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V, any two linearly independent generating setGenerating setIn mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
s (in other words, any two bases) have the same cardinality.
If V is finitely generated, then it has a finite basis, and the result says that any two bases have the same number of elements.
While the proof of the existence of a basis for any vector space in the general case requires Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
and is in fact equivalent to the axiom of choice, the uniqueness of the cardinality of the basis requires only the ultrafilter lemma , which is strictly weaker (the proof given below, however, assumes trichotomy, i.e., that all cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s are comparable, a statement which is also equivalent to the axiom of choice). The theorem can be generalized to arbitrary R-modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
for rings R having invariant basis number
Invariant basis number
In mathematics, the invariant basis number property of a ring R is the property that all free modules over R are similarly well-behaved as vector spaces, with respect to the uniqueness of their ranks.-Definition:...
.
The theorem for finitely generated case can be proved with elementary arguments of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, and requires no forms of the axiom of choice.
Proof
Assume that { ai: i ∈ I } and{ bj: j ∈ J } are both bases, with the cardinality of I bigger than the cardinality of J. From this assumption we will derive a contradiction.
Case 1
Assume that I is infinite.Every bj can be written as a finite sum
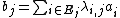 , where
, where 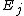 is a finite subset of
is a finite subset of 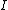 .
.Since the cardinality of I is greater than that of J and the Ej's are finite subsets of I, the cardinality of I is also bigger than the cardinality of
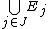 . (Note that this argument works only for infinite I.) So there is some
. (Note that this argument works only for infinite I.) So there is some 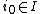 which does not appear
which does not appearin any
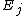 . The corresponding
. The corresponding 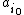 can be expressed as a finite linear combination of
can be expressed as a finite linear combination of 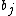 's, which in turn can be expressed as finite linear combination of
's, which in turn can be expressed as finite linear combination of 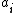 's, not involving
's, not involving  . Hence
. Hence 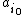 is linearly dependent on the other
is linearly dependent on the other 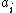 's.
's.Case 2
Now assume that I is finite and of cardinality bigger than the cardinality of J. Write m and n for the cardinalities of I and J, respectively.Every ai can be written as a sum
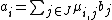
The matrix
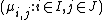 has n columns (the j-th column is the
has n columns (the j-th column is them-tuple
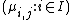 ), so it has rank at most n. This means that its m rows cannot be linearly independent. Write
), so it has rank at most n. This means that its m rows cannot be linearly independent. Write 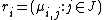 for the i-th row, then there is a nontrivial
for the i-th row, then there is a nontriviallinear combination
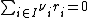
But then also
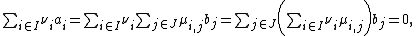
so the
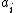 are linearly dependent.
are linearly dependent.Alternative Proof
The proof above uses several non-trivial results. If these results are not carefully established in advance, the proof may give rise to circular reasoning. Here is a proof of the finite case which requires less prior development.Theorem 1: If
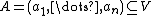 is a linearly independent tuple
is a linearly independent tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
in a vector space
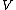 , and
, and 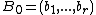 is a tuple that spans
is a tuple that spans 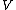 , then
, then 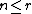 . The argument is as follows:
. The argument is as follows:Since
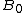 spans
spans 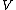 , the tuple
, the tuple 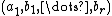 also spans. Since
also spans. Since 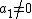 (because
(because 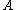 is linearly independent), there is at least one
is linearly independent), there is at least one 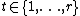 such that
such that 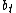 can be written as a linear combination of
can be written as a linear combination of 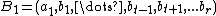 . Thus,
. Thus, 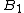 is a spanning tuple, and its length is the same as
is a spanning tuple, and its length is the same as 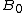 's.
's.Repeat this process. Because
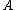 is linearly independent, we can always remove an element from the list
is linearly independent, we can always remove an element from the list 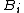 which is not one of the
which is not one of the 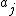 's that we prepended to the list in a prior step (because
's that we prepended to the list in a prior step (because 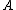 is linearly independent, and so there must be some nonzero coefficient in front of one of the
is linearly independent, and so there must be some nonzero coefficient in front of one of the 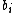 's). Thus, after
's). Thus, after  iterations, the result will be a tuple
iterations, the result will be a tuple 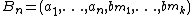 (possibly with
(possibly with 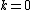 ) of length
) of length  . In particular,
. In particular, 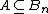 , so
, so 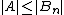 , i.e.,
, i.e., 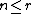 .
.To prove the finite case of the dimension theorem from this, suppose that
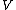 is a vector space and
is a vector space and 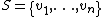 and
and 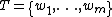 are both bases of
are both bases of 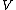 . Since
. Since 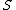 is linearly independent and
is linearly independent and 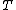 spans, we can apply Theorem 1 to get
spans, we can apply Theorem 1 to get  . And since
. And since 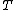 is linearly independent and
is linearly independent and 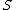 spans, we get
spans, we get 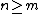 . From these, we get
. From these, we get  .
.Kernel extension theorem for vector spaces
This application of the dimension theorem is sometimes itself called the dimension theorem. Let- T: U → V
be a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
. Then
- dim(range(T)) + dim(kernel(T)) = dim(U),
that is, the dimension of U is equal to the dimension of the transformation's range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
plus the dimension of the kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
. See rank-nullity theorem
Rank-nullity theorem
In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
for a fuller discussion.

