
Perverse sheaf
Encyclopedia
The mathematical term perverse sheaves refers to a certain abelian category
associated to a topological space X, which may be a real or complex manifold, or a more general Topologically stratified space
, usually singular. This concept was introduced by Zoghman Mebkhout
in his thesis and then further developed by Joseph Bernstein
, Alexander Beilinson
, Pierre Deligne
, and Ofer Gabber (1982) as a formalisation of the Riemann-Hilbert correspondence, which related the topology of singular spaces (intersection homology of Mark Goresky
and Robert MacPherson) and the algebraic theory of differential equations (microlocal calculus and holonomic D-module
s of Joseph Bernstein
, Masaki Kashiwara
and Takahira Kawai). It was clear from the outset that perverse sheaves are fundamental mathematical objects at the crossroads of algebraic geometry
, topology
, analysis and differential equations. They also play an important role in number theory
, algebra, and representation theory
.
The Beilinson-Bernstein-Deligne definition of a perverse sheaf proceeds through the machinery of triangulated categories in homological algebra
and has very strong algebraic flavour, although the main examples arising from Goresky-MacPherson theory are topological in nature. This motivated MacPherson to recast the whole theory in geometric terms on a basis of Morse theory
. For many applications in representation theory, perverse sheaves can be treated as a 'black box', a category with certain formal properties.
In the Riemann-Hilbert correspondence, perverse sheaves correspond to holonomic D-module
s. This application established the notion of perverse sheaf as occurring 'in nature'.
of sheaves with constructible cohomology on a space X such that the set of points x with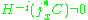 or
or 
has dimension at most 2i, for all i. Here jx is the inclusion map of the point x.
The category of perverse sheaves is an abelian subcategory of the (non-abelian) derived category of sheaves,
equal to the core of a suitable t-structure, and is preserved by Verdier duality
.
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
associated to a topological space X, which may be a real or complex manifold, or a more general Topologically stratified space
Topologically stratified space
In topology, a branch of mathematics, a topologically stratified space is a space X that has been decomposed into pieces called strata; these strata are topological manifolds and are required to fit together in a certain way...
, usually singular. This concept was introduced by Zoghman Mebkhout
Zoghman Mebkhout
Zoghman Mebkhout is an Algerian mathematician known for his work in algebraic analysis, geometry, and representation theory, more precisely on the theory of D-modules ....
in his thesis and then further developed by Joseph Bernstein
Joseph Bernstein
Joseph Bernstein is an Israeli mathematician working at Tel Aviv University. He works in algebraic geometry, representation theory, and number theory....
, Alexander Beilinson
Alexander Beilinson
Alexander A. Beilinson is the David and Mary Winton Green University Professor at the University of Chicago and works on mathematics. His research has spanned representation theory, algebraic geometry and mathematical physics...
, Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
, and Ofer Gabber (1982) as a formalisation of the Riemann-Hilbert correspondence, which related the topology of singular spaces (intersection homology of Mark Goresky
Mark Goresky
Robert Mark Goresky is a Canadian mathematician who invented intersection homology with Robert MacPherson.He received his Ph.D. from Brown University in 1976. His thesis, titled Geometric Cohomology and Homology of Stratified Objects, was written under the direction of MacPherson...
and Robert MacPherson) and the algebraic theory of differential equations (microlocal calculus and holonomic D-module
D-module
In mathematics, a D-module is a module over a ring D of differential operators. The major interest of such D-modules is as an approach to the theory of linear partial differential equations...
s of Joseph Bernstein
Joseph Bernstein
Joseph Bernstein is an Israeli mathematician working at Tel Aviv University. He works in algebraic geometry, representation theory, and number theory....
, Masaki Kashiwara
Masaki Kashiwara
is a Japanese mathematician. He was a student of Mikio Sato at the University of Tokyo. Sato and Kashiwara have collaborated on algebraic analysis and D-module theory.He is a member of the French Academy of Sciences.- Concepts named after Kashiwara :...
and Takahira Kawai). It was clear from the outset that perverse sheaves are fundamental mathematical objects at the crossroads of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, analysis and differential equations. They also play an important role in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, algebra, and representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
.
Preliminary remarks
The name perverse sheaf is a bit of a misnomer for neither are they sheaves, in the ordinary, stylistic, genealogical or literal senses, nor are they perverse. The justification is that perverse sheaves have several features in common with sheaves: they form an abelian category, you can take their cohomology, and to construct one, it suffices to construct it locally everywhere. The adjective perverse originates in the intersection homology theory, and its origin was explained by .The Beilinson-Bernstein-Deligne definition of a perverse sheaf proceeds through the machinery of triangulated categories in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
and has very strong algebraic flavour, although the main examples arising from Goresky-MacPherson theory are topological in nature. This motivated MacPherson to recast the whole theory in geometric terms on a basis of Morse theory
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
. For many applications in representation theory, perverse sheaves can be treated as a 'black box', a category with certain formal properties.
In the Riemann-Hilbert correspondence, perverse sheaves correspond to holonomic D-module
D-module
In mathematics, a D-module is a module over a ring D of differential operators. The major interest of such D-modules is as an approach to the theory of linear partial differential equations...
s. This application established the notion of perverse sheaf as occurring 'in nature'.
Definition
A perverse sheaf is an object C of the bounded derived categoryDerived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of sheaves with constructible cohomology on a space X such that the set of points x with
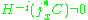 or
or 
has dimension at most 2i, for all i. Here jx is the inclusion map of the point x.
The category of perverse sheaves is an abelian subcategory of the (non-abelian) derived category of sheaves,
equal to the core of a suitable t-structure, and is preserved by Verdier duality
Verdier duality
In mathematics, Verdier duality is a generalization of the Poincaré duality of manifolds to locally compact spaces with singularities. Verdier duality was introduced by , as an analog for locally compact spaces of the coherent duality for schemes due to Grothendieck...
.

