
D-brane
Encyclopedia
In string theory
, D-branes are a class of extended objects upon which open string
s can end with Dirichlet boundary condition
s, after which they are named. D-branes were discovered by Dai, Leigh
and Polchinski
, and independently by Hořava
in 1989. In 1995, Polchinski identified D-branes with black p-brane solutions of supergravity
, a discovery that triggered the Second Superstring Revolution and led to both holographic
and M-theory
dualities.
D-branes are typically classified by their spatial dimension
, which is indicated by a number written after the D. A D0-brane is a single point, a D1-brane is a line (sometimes called a "D-string"), a D2-brane is a plane, and a D25-brane fills the highest-dimensional space considered in bosonic string theory
. There are also instanton
ic D(-1)-branes, which are localized in both space and time.
, corresponding to free endpoints moving through spacetime at the speed of light, or the Dirichlet boundary conditions, which pin the string endpoint. Each coordinate of the string must satisfy one or the other of these conditions. There can also exist strings with mixed boundary conditions, where the two endpoints satisfy NN, DD, ND and DN boundary conditions. If p spatial dimensions satisfy the Neumann boundary condition, then the string endpoint is confined to move within a p-dimensional hyperplane. This hyperplane provides one description of a Dp-brane.
Although rigid in the limit of zero coupling, the spectrum of open strings ending on a D-brane contains modes associated with its fluctuations, implying that D-branes are dynamical objects. When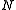 D-branes are nearly coincident, the spectrum of strings stretching between them becomes very rich. One set of modes produce a non-abelian gauge theory on the world-volume. Another set of modes is an
D-branes are nearly coincident, the spectrum of strings stretching between them becomes very rich. One set of modes produce a non-abelian gauge theory on the world-volume. Another set of modes is an 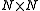 dimensional matrix for each transverse dimension of the brane. If these matrices commute, they may be diagonalized, and the eigenvalues define the position of the
dimensional matrix for each transverse dimension of the brane. If these matrices commute, they may be diagonalized, and the eigenvalues define the position of the 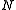 D-branes in space. More generally, the branes are described by non-commutative geometry, which allows exotic behavior such as the Myers effect, in which a collection of Dp-branes expand into a D(p+2)-brane.
D-branes in space. More generally, the branes are described by non-commutative geometry, which allows exotic behavior such as the Myers effect, in which a collection of Dp-branes expand into a D(p+2)-brane.
Tachyon condensation
is a central concept in this field. Ashoke Sen
has argued that in Type IIB string theory
, tachyon condensation allows (in the absence of Neveu-Schwarz 3-form
flux) an arbitrary D-brane configuration to be obtained from a stack of D9 and anti D9-branes. Edward Witten
has shown that such configurations will be classified by the K-theory
of the spacetime
. Tachyon condensation is still very poorly understood. This is due to the lack of an exact string field theory that would describe the off-shell evolution of the tachyon.
. Because string theory implies that the Universe has more dimensions than we expect—26 for bosonic string theories
and 10 for superstring theories
—we have to find a reason why the extra dimensions are not apparent. One possibility would be that the visible Universe is in fact a very large D-brane extending over three spatial dimensions. Material objects, made of open strings, are bound to the D-brane, and cannot move "at right angles to reality" to explore the Universe outside the brane. This scenario is called a brane cosmology
. The force of gravity is not due to open strings; the graviton
s which carry gravitational forces are vibrational states of closed strings. Because closed strings do not have to be attached to D-branes, gravitational effects could depend upon the extra dimensions at right angles to the brane.
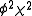 . Thus, as the field
. Thus, as the field 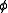 (separation of the branes) changes, the mass of the field
(separation of the branes) changes, the mass of the field 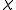 changes. This induces open string production and as a result the two scattering branes will be trapped.
changes. This induces open string production and as a result the two scattering branes will be trapped.
 and the
and the 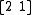 sectors. In addition, a string may begin and end on the same brane, giving
sectors. In addition, a string may begin and end on the same brane, giving 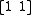 and
and  sectors. (The numbers inside the brackets are called Chan-Paton indices
sectors. (The numbers inside the brackets are called Chan-Paton indices
, but they are really just labels identifying the branes.) A string in either the or the
or the  sector has a minimum length: it cannot be shorter than the separation between the branes. All strings have some tension, against which one must pull to lengthen the object; this pull does work on the string, adding to its energy. Because string theories are by nature relativistic
sector has a minimum length: it cannot be shorter than the separation between the branes. All strings have some tension, against which one must pull to lengthen the object; this pull does work on the string, adding to its energy. Because string theories are by nature relativistic
, adding energy to a string is equivalent to adding mass, by Einstein's relation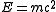 . Therefore, the separation between D-branes controls the minimum mass open strings may have.
. Therefore, the separation between D-branes controls the minimum mass open strings may have.
Furthermore, affixing a string's endpoint to a brane influences the way the string can move and vibrate. Because particle states "emerge" from the string theory as the different vibrational states the string can experience, the arrangement of D-branes controls the types of particles present in the theory. The simplest case is the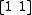 sector for a Dp-brane, that is to say the strings which begin and end on any particular D-brane of p dimensions. Examining the consequences of the Nambu-Goto action
sector for a Dp-brane, that is to say the strings which begin and end on any particular D-brane of p dimensions. Examining the consequences of the Nambu-Goto action
(and applying the rules of quantum mechanics
to quantize
the string), one finds that among the spectrum of particles is one resembling the photon
, the fundamental quantum of the electromagnetic field. The resemblance is precise: a p-dimensional version of the electromagnetic field, obeying a p-dimensional analogue of Maxwell's equations
, exists on every Dp-brane.
In this sense, then, one can say that string theory "predicts" electromagnetism: D-branes are a necessary part of the theory if we permit open strings to exist, and all D-branes carry an electromagnetic field on their volume.
Other particle states originate from strings beginning and ending on the same D-brane. Some correspond to massless particles like the photon; also in this group are a set of massless scalar particles. If a Dp-brane is embedded in a spacetime of d spatial dimensions, the brane carries (in addition to its Maxwell field) a set of d - p massless scalars
(particles which do not have polarizations like the photons making up light). Intriguingly, there are just as many massless scalars as there are directions perpendicular to the brane; the geometry of the brane arrangement is closely related to the quantum field theory
of the particles existing on it. In fact, these massless scalars are Goldstone excitations of the brane, corresponding to the different ways the symmetry of empty space can be broken. Placing a D-brane in a universe breaks the symmetry among locations, because it defines a particular place, assigning a special meaning to a particular location along each of the d - p directions perpendicular to the brane.
The quantum version of Maxwell's electromagnetism is only one kind of gauge theory
, a U(1)
gauge theory where the gauge group
is made of unitary matrices
of order 1. D-branes can be used to generate gauge theories of higher order, in the following way:
Consider a group of N separate Dp-branes, arranged in parallel for simplicity. The branes are labeled 1,2,...,N for convenience. Open strings in this system exist in one of many sectors: the strings beginning and ending on some brane i give that brane a Maxwell field and some massless scalar fields on its volume. The strings stretching from brane i to another brane j have more intriguing properties. For starters, it is worthwhile to ask which sectors of strings can interact with one another. One straightforward mechanism for a string interaction is for two strings to join endpoints (or, conversely, for one string to "split down the middle" and make two "daughter" strings). Since endpoints are restricted to lie on D-branes, it is evident that a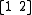 string may interact with a
string may interact with a 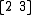 string, but not with a
string, but not with a  or a
or a 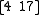 one. The masses of these strings will be influenced by the separation between the branes, as discussed above, so for simplicity's sake we can imagine the branes squeezed closer and closer together, until they lie atop one another. If we regard two overlapping branes as distinct objects, then we still have all the sectors we had before, but without the effects due to the brane separations.
one. The masses of these strings will be influenced by the separation between the branes, as discussed above, so for simplicity's sake we can imagine the branes squeezed closer and closer together, until they lie atop one another. If we regard two overlapping branes as distinct objects, then we still have all the sectors we had before, but without the effects due to the brane separations.
The zero-mass states in the open-string particle spectrum for a system of N coincident D-branes yields a set of interacting quantum fields which is exactly a U(N) gauge theory. (The string theory does contain other interactions, but they are only detectable at very high energies.) Gauge theories were not invented starting with bosonic or fermionic strings; they originated from a different area of physics, and have become quite useful in their own right. If nothing else, the relation between D-brane geometry and gauge theory offers a useful pedagogical tool for explaining gauge interactions, even if string theory fails to be the "theory of everything".
s. Since the 1970s, scientists have debated the problem of black holes having entropy
. Consider, as a thought experiment
, dropping an amount of hot gas into a black hole. Since the gas cannot escape from the hole's gravitational pull, its entropy would seem to have vanished from the universe. In order to maintain the second law of thermodynamics
, one must postulate that the black hole gained whatever entropy the infalling gas originally had. Attempting to apply quantum mechanics
to the study of black holes, Stephen Hawking
discovered that a hole should emit energy with the characteristic spectrum of thermal radiation. The characteristic temperature of this Hawking radiation
is given by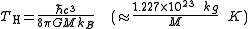 ,
,
where G is Newton
's gravitational constant
, M is the black hole's mass and kB is Boltzmann's constant.
Using this expression for the Hawking temperature, and assuming that a zero-mass black hole has zero entropy, one can use thermodynamic arguments to derive the "Bekenstein
entropy":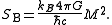
The Bekenstein entropy is proportional to the black hole mass squared; because the Schwarzschild radius
is proportional to the mass, the Bekenstein entropy is proportional to the black hole's surface area. In fact,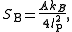
where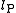 is the Planck length.
is the Planck length.
The concept of black hole entropy poses some interesting conundra. In an ordinary situation, a system has entropy when a large number of different "microstates" can satisfy the same macroscopic condition. For example, given a box full of gas, many different arrangements of the gas atoms can have the same total energy. However, a black hole was believed to be a featureless object (in John Wheeler
's catchphrase, "Black holes have no hair
"). What, then, are the "degrees of freedom" which can give rise to black hole entropy?
String theorists have constructed models in which a black hole is a very long (and hence very massive) string. This model gives rough agreement with the expected entropy of a Schwarzschild black hole, but an exact proof has yet to be found one way or the other. The chief difficulty is that it is relatively easy to count the degrees of freedom quantum strings possess if they do not interact with one another. This is analogous to the ideal gas
studied in introductory thermodynamics: the easiest situation to model is when the gas atoms do not have interactions among themselves. Developing the kinetic theory
of gases in the case where the gas atoms or molecules experience inter-particle forces (like the van der Waals force
) is more difficult. However, a world without interactions is an uninteresting place: most significantly for the black hole problem, gravity is an interaction, and so if the "string coupling" is turned off, no black hole could ever arise. Therefore, calculating black hole entropy requires working in a regime where string interactions exist.
Extending the simpler case of non-interacting strings to the regime where a black hole could exist requires supersymmetry
. In certain cases, the entropy calculation done for zero string coupling remains valid when the strings interact. The challenge for a string theorist is to devise a situation in which a black hole can exist which does not "break" supersymmetry. In recent years, this has been done by building black holes out of D-branes. Calculating the entropies of these hypothetical holes gives results which agree with the expected Bekenstein entropy. Unfortunately, the cases studied so far all involve higher-dimensional spaces — D5-branes in nine-dimensional space, for example. They do not directly apply to the familiar case, the Schwarzschild black holes observed in our own universe.
in 1977 as a means of introducing point-like structure into string theory, in an attempt to construct a string theory of the strong interaction
. String compactifications studied by Harvey and Minahan, Ishibashi and Onogi, and Pradisi and Sagnotti in 1987-89 also employed Dirichlet boundary conditions.
The fact that T-duality
interchanges the usual Neumann boundary conditions with Dirichlet boundary conditions was discovered independently by Horava and by Dai, Leigh, and Polchinski
in 1989; this result implies that such boundary conditions must necessarily appear in regions of the moduli space
of any open string theory. The Dai et al. paper also notes that the locus of the Dirichlet boundary conditions is dynamical, and coins the term Dirichlet-brane (D-brane) for the resulting object (this paper also coins orientifold
for another object that arises under string T-duality). A 1989 paper by Leigh showed that D-brane dynamics are governed by the Dirac-Born-Infeld action. D-instantons were extensively studied by Green in the early 1990s, and were shown by Polchinski in 1994 to produce the e^{-1/g} nonperturbative string effects anticipated by Shenker. In 1995 Polchinski showed that D-branes are the sources of electric and magnetic Ramond-Ramond field
s that are required by string duality, leading to rapid progress in the nonperturbative understanding of string theory.
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, D-branes are a class of extended objects upon which open string
String (physics)
A string is a hypothetical vibrating one-dimensional sub-atomic structure and one of the main objects of study in string theory, a branch of theoretical physics. There are different string theories, many of which are unified by M-theory. A string is an object with a one-dimensional spatial extent,...
s can end with Dirichlet boundary condition
Dirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
s, after which they are named. D-branes were discovered by Dai, Leigh
Robert Leigh
Robert Leigh is a physicist working on string theory.He obtained his B.Sc. degree from the University of Guelph in 1986, and his Ph.D. from the University of Texas at Austin in 1991, working with Joe Polchinski...
and Polchinski
Joseph Polchinski
Joseph Polchinski is a physicist working on string theory. He graduated from Canyon del Oro High School in Tucson, Arizona in 1971, obtained his B.S. degree from Caltech in 1975, and his Ph.D. from the University of California, Berkeley in 1980 under the supervision of Stanley Mandelstam...
, and independently by Hořava
Petr Horava
Petr Hořava is a Czech string theorist. He is currently a professor of physics at the University of California, Berkeley, where he frequently teaches courses on quantum field theory and string theory...
in 1989. In 1995, Polchinski identified D-branes with black p-brane solutions of supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
, a discovery that triggered the Second Superstring Revolution and led to both holographic
Holographic principle
The holographic principle is a property of quantum gravity and string theories which states that the description of a volume of space can be thought of as encoded on a boundary to the region—preferably a light-like boundary like a gravitational horizon...
and M-theory
M-theory
In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
dualities.
D-branes are typically classified by their spatial dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
, which is indicated by a number written after the D. A D0-brane is a single point, a D1-brane is a line (sometimes called a "D-string"), a D2-brane is a plane, and a D25-brane fills the highest-dimensional space considered in bosonic string theory
Bosonic string theory
Bosonic string theory is the original version of string theory, developed in the late 1960s.In the early 1970s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory became the real focus...
. There are also instanton
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
ic D(-1)-branes, which are localized in both space and time.
Theoretical background
The equations of motion of string theory require that the endpoints of an open string (a string with endpoints) satisfy one of two types of boundary conditions: The Neumann boundary conditionNeumann boundary condition
In mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
, corresponding to free endpoints moving through spacetime at the speed of light, or the Dirichlet boundary conditions, which pin the string endpoint. Each coordinate of the string must satisfy one or the other of these conditions. There can also exist strings with mixed boundary conditions, where the two endpoints satisfy NN, DD, ND and DN boundary conditions. If p spatial dimensions satisfy the Neumann boundary condition, then the string endpoint is confined to move within a p-dimensional hyperplane. This hyperplane provides one description of a Dp-brane.
Although rigid in the limit of zero coupling, the spectrum of open strings ending on a D-brane contains modes associated with its fluctuations, implying that D-branes are dynamical objects. When
 D-branes are nearly coincident, the spectrum of strings stretching between them becomes very rich. One set of modes produce a non-abelian gauge theory on the world-volume. Another set of modes is an
D-branes are nearly coincident, the spectrum of strings stretching between them becomes very rich. One set of modes produce a non-abelian gauge theory on the world-volume. Another set of modes is an 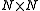 dimensional matrix for each transverse dimension of the brane. If these matrices commute, they may be diagonalized, and the eigenvalues define the position of the
dimensional matrix for each transverse dimension of the brane. If these matrices commute, they may be diagonalized, and the eigenvalues define the position of the 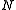 D-branes in space. More generally, the branes are described by non-commutative geometry, which allows exotic behavior such as the Myers effect, in which a collection of Dp-branes expand into a D(p+2)-brane.
D-branes in space. More generally, the branes are described by non-commutative geometry, which allows exotic behavior such as the Myers effect, in which a collection of Dp-branes expand into a D(p+2)-brane.Tachyon condensation
Tachyon condensation
In particle physics, theoretical processes that eliminate or resolve particles or fields into better understood phenomena are called, by extension and metaphor with the macroscopic process, "condensation"...
is a central concept in this field. Ashoke Sen
Ashoke Sen
Ashoke Sen , FRS, is an Indian theoretical physicist. He has made a number of major original contributions to the subject of string theory, including his landmark paper on strong-weak coupling duality or S-duality, which was influential in changing the course of research in the field...
has argued that in Type IIB string theory
Type II string theory
In theoretical physics, type II string theory is a unified term that includes both type IIA strings and type IIB strings. These account for two of the five consistent superstring theories in ten dimensions. Both theories have the maximal amount of supersymmetry — namely 32 supercharges...
, tachyon condensation allows (in the absence of Neveu-Schwarz 3-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
flux) an arbitrary D-brane configuration to be obtained from a stack of D9 and anti D9-branes. Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
has shown that such configurations will be classified by the K-theory
K-theory (physics)
In string theory, the K-theory classification refers to a conjectured application of K-theory to superstrings, to classify the allowed Ramond-Ramond field strengths as well as the charges of stable D-branes....
of the spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. Tachyon condensation is still very poorly understood. This is due to the lack of an exact string field theory that would describe the off-shell evolution of the tachyon.
Braneworld cosmology
This has implications for physical cosmologyPhysical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
. Because string theory implies that the Universe has more dimensions than we expect—26 for bosonic string theories
Bosonic string theory
Bosonic string theory is the original version of string theory, developed in the late 1960s.In the early 1970s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory became the real focus...
and 10 for superstring theories
Superstring theory
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...
—we have to find a reason why the extra dimensions are not apparent. One possibility would be that the visible Universe is in fact a very large D-brane extending over three spatial dimensions. Material objects, made of open strings, are bound to the D-brane, and cannot move "at right angles to reality" to explore the Universe outside the brane. This scenario is called a brane cosmology
Brane cosmology
Brane cosmology refers to several theories in particle physics and cosmology motivated by, but not exclusively derived from, superstring theory and M-theory.-Brane and bulk:...
. The force of gravity is not due to open strings; the graviton
Graviton
In physics, the graviton is a hypothetical elementary particle that mediates the force of gravitation in the framework of quantum field theory. If it exists, the graviton must be massless and must have a spin of 2...
s which carry gravitational forces are vibrational states of closed strings. Because closed strings do not have to be attached to D-branes, gravitational effects could depend upon the extra dimensions at right angles to the brane.
D-brane scattering
When two D-branes approach each other the interaction is captured by the one loop annulus amplitude of strings between the two branes. The scenario of two parallel branes approaching each other at a constant velocity can be mapped to the problem of two stationary branes that are rotated relative to each other by some angle. The annulus amplitude yields singularities that correspond to the on-shell production of open strings stretched between the two branes. This is true irrespective of the charge of the D-branes. At non-relativistic scattering velocities the open strings may be described by a low-energy effective action that contains two complex scalar fields that are coupled via a term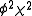 . Thus, as the field
. Thus, as the field 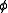 (separation of the branes) changes, the mass of the field
(separation of the branes) changes, the mass of the field 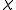 changes. This induces open string production and as a result the two scattering branes will be trapped.
changes. This induces open string production and as a result the two scattering branes will be trapped.Gauge theories
The arrangement of D-branes constricts the types of string states which can exist in a system. For example, if we have two parallel D2-branes, we can easily imagine strings stretching from brane 1 to brane 2 or vice versa. (In most theories, strings are oriented objects: each one carries an "arrow" defining a direction along its length.) The open strings permissible in this situation then fall into two categories, or "sectors": those originating on brane 1 and terminating on brane 2, and those originating on brane 2 and terminating on brane 1. Symbolically, we say we have the and the
and the 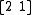 sectors. In addition, a string may begin and end on the same brane, giving
sectors. In addition, a string may begin and end on the same brane, giving 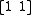 and
and  sectors. (The numbers inside the brackets are called Chan-Paton indices
sectors. (The numbers inside the brackets are called Chan-Paton indicesChan-Paton factor
In theoretical physics, the Chan–Paton factor is a multivalued index associated with the endpoints of an open string. An open string can be interpreted as a fluxtube connecting a quark and its antiparticle...
, but they are really just labels identifying the branes.) A string in either the
 or the
or the  sector has a minimum length: it cannot be shorter than the separation between the branes. All strings have some tension, against which one must pull to lengthen the object; this pull does work on the string, adding to its energy. Because string theories are by nature relativistic
sector has a minimum length: it cannot be shorter than the separation between the branes. All strings have some tension, against which one must pull to lengthen the object; this pull does work on the string, adding to its energy. Because string theories are by nature relativisticSpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, adding energy to a string is equivalent to adding mass, by Einstein's relation
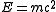 . Therefore, the separation between D-branes controls the minimum mass open strings may have.
. Therefore, the separation between D-branes controls the minimum mass open strings may have.Furthermore, affixing a string's endpoint to a brane influences the way the string can move and vibrate. Because particle states "emerge" from the string theory as the different vibrational states the string can experience, the arrangement of D-branes controls the types of particles present in the theory. The simplest case is the
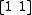 sector for a Dp-brane, that is to say the strings which begin and end on any particular D-brane of p dimensions. Examining the consequences of the Nambu-Goto action
sector for a Dp-brane, that is to say the strings which begin and end on any particular D-brane of p dimensions. Examining the consequences of the Nambu-Goto actionNambu-Goto action
The Nambu–Goto action is the simplest invariant action in bosonic string theory, and is also used in other theories that investigate string-like objects . It is the starting point of the analysis of zero-thickness string behavior, using the principles of Lagrangian mechanics...
(and applying the rules of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
to quantize
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
the string), one finds that among the spectrum of particles is one resembling the photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
, the fundamental quantum of the electromagnetic field. The resemblance is precise: a p-dimensional version of the electromagnetic field, obeying a p-dimensional analogue of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, exists on every Dp-brane.
In this sense, then, one can say that string theory "predicts" electromagnetism: D-branes are a necessary part of the theory if we permit open strings to exist, and all D-branes carry an electromagnetic field on their volume.
Other particle states originate from strings beginning and ending on the same D-brane. Some correspond to massless particles like the photon; also in this group are a set of massless scalar particles. If a Dp-brane is embedded in a spacetime of d spatial dimensions, the brane carries (in addition to its Maxwell field) a set of d - p massless scalars
Scalar field theory
In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
(particles which do not have polarizations like the photons making up light). Intriguingly, there are just as many massless scalars as there are directions perpendicular to the brane; the geometry of the brane arrangement is closely related to the quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
of the particles existing on it. In fact, these massless scalars are Goldstone excitations of the brane, corresponding to the different ways the symmetry of empty space can be broken. Placing a D-brane in a universe breaks the symmetry among locations, because it defines a particular place, assigning a special meaning to a particular location along each of the d - p directions perpendicular to the brane.
The quantum version of Maxwell's electromagnetism is only one kind of gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, a U(1)
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
gauge theory where the gauge group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is made of unitary matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of order 1. D-branes can be used to generate gauge theories of higher order, in the following way:
Consider a group of N separate Dp-branes, arranged in parallel for simplicity. The branes are labeled 1,2,...,N for convenience. Open strings in this system exist in one of many sectors: the strings beginning and ending on some brane i give that brane a Maxwell field and some massless scalar fields on its volume. The strings stretching from brane i to another brane j have more intriguing properties. For starters, it is worthwhile to ask which sectors of strings can interact with one another. One straightforward mechanism for a string interaction is for two strings to join endpoints (or, conversely, for one string to "split down the middle" and make two "daughter" strings). Since endpoints are restricted to lie on D-branes, it is evident that a
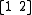 string may interact with a
string may interact with a 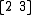 string, but not with a
string, but not with a  or a
or a 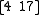 one. The masses of these strings will be influenced by the separation between the branes, as discussed above, so for simplicity's sake we can imagine the branes squeezed closer and closer together, until they lie atop one another. If we regard two overlapping branes as distinct objects, then we still have all the sectors we had before, but without the effects due to the brane separations.
one. The masses of these strings will be influenced by the separation between the branes, as discussed above, so for simplicity's sake we can imagine the branes squeezed closer and closer together, until they lie atop one another. If we regard two overlapping branes as distinct objects, then we still have all the sectors we had before, but without the effects due to the brane separations.The zero-mass states in the open-string particle spectrum for a system of N coincident D-branes yields a set of interacting quantum fields which is exactly a U(N) gauge theory. (The string theory does contain other interactions, but they are only detectable at very high energies.) Gauge theories were not invented starting with bosonic or fermionic strings; they originated from a different area of physics, and have become quite useful in their own right. If nothing else, the relation between D-brane geometry and gauge theory offers a useful pedagogical tool for explaining gauge interactions, even if string theory fails to be the "theory of everything".
Black holes
Another important use of D-branes has been in the study of black holeBlack hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s. Since the 1970s, scientists have debated the problem of black holes having entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
. Consider, as a thought experiment
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
, dropping an amount of hot gas into a black hole. Since the gas cannot escape from the hole's gravitational pull, its entropy would seem to have vanished from the universe. In order to maintain the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
, one must postulate that the black hole gained whatever entropy the infalling gas originally had. Attempting to apply quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
to the study of black holes, Stephen Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
discovered that a hole should emit energy with the characteristic spectrum of thermal radiation. The characteristic temperature of this Hawking radiation
Hawking radiation
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
is given by
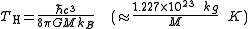 ,
,where G is Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, M is the black hole's mass and kB is Boltzmann's constant.
Using this expression for the Hawking temperature, and assuming that a zero-mass black hole has zero entropy, one can use thermodynamic arguments to derive the "Bekenstein
Jacob Bekenstein
Jacob David Bekenstein is an Israeli theoretical physicist who has contributed to the foundation of black hole thermodynamics and to other aspects of the connections between information and gravitation.-Biography:...
entropy":
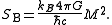
The Bekenstein entropy is proportional to the black hole mass squared; because the Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
is proportional to the mass, the Bekenstein entropy is proportional to the black hole's surface area. In fact,
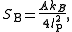
where
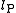 is the Planck length.
is the Planck length.The concept of black hole entropy poses some interesting conundra. In an ordinary situation, a system has entropy when a large number of different "microstates" can satisfy the same macroscopic condition. For example, given a box full of gas, many different arrangements of the gas atoms can have the same total energy. However, a black hole was believed to be a featureless object (in John Wheeler
John Wheeler
John Wheeler may refer to:* John Wheeler , American Emmy Award-winning audio/video engineer* John Wheeler , Union officer in the Civil War; killed at Gettysburg* John Wheeler John Wheeler may refer to:* John Wheeler (audio/video technologist) (born 1957), American Emmy Award-winning audio/video...
's catchphrase, "Black holes have no hair
No hair theorem
The no-hair theorem postulates that all black hole solutions of the Einstein-Maxwell equations of gravitation and electromagnetism in general relativity can be completely characterized by only three externally observable classical parameters: mass, electric charge, and angular momentum...
"). What, then, are the "degrees of freedom" which can give rise to black hole entropy?
String theorists have constructed models in which a black hole is a very long (and hence very massive) string. This model gives rough agreement with the expected entropy of a Schwarzschild black hole, but an exact proof has yet to be found one way or the other. The chief difficulty is that it is relatively easy to count the degrees of freedom quantum strings possess if they do not interact with one another. This is analogous to the ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
studied in introductory thermodynamics: the easiest situation to model is when the gas atoms do not have interactions among themselves. Developing the kinetic theory
Kinetic theory
The kinetic theory of gases describes a gas as a large number of small particles , all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container...
of gases in the case where the gas atoms or molecules experience inter-particle forces (like the van der Waals force
Van der Waals force
In physical chemistry, the van der Waals force , named after Dutch scientist Johannes Diderik van der Waals, is the sum of the attractive or repulsive forces between molecules other than those due to covalent bonds or to the electrostatic interaction of ions with one another or with neutral...
) is more difficult. However, a world without interactions is an uninteresting place: most significantly for the black hole problem, gravity is an interaction, and so if the "string coupling" is turned off, no black hole could ever arise. Therefore, calculating black hole entropy requires working in a regime where string interactions exist.
Extending the simpler case of non-interacting strings to the regime where a black hole could exist requires supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
. In certain cases, the entropy calculation done for zero string coupling remains valid when the strings interact. The challenge for a string theorist is to devise a situation in which a black hole can exist which does not "break" supersymmetry. In recent years, this has been done by building black holes out of D-branes. Calculating the entropies of these hypothetical holes gives results which agree with the expected Bekenstein entropy. Unfortunately, the cases studied so far all involve higher-dimensional spaces — D5-branes in nine-dimensional space, for example. They do not directly apply to the familiar case, the Schwarzschild black holes observed in our own universe.
History
Dirichlet boundary conditions and D-branes had a long `pre-history' before their full significance was recognized. Mixed Dirichlet/Neumann boundary conditions were first considered by Warren Siegel in 1976 as a means of lowering the critical dimension of open string theory from 26 or 10 to 4 (Siegel also cites unpublished work by Halpern, and a 1974 paper by Chodos and Thorn, but a reading of the latter paper shows that it is actually concerned with linear dilation backgrounds, not Dirichlet boundary conditions). This paper, though prescient, was little-noted in its time (a 1985 parody by Siegel, `The Super-g String,' contains an almost dead-on description of braneworlds). Dirichlet conditions for all coordinates including Euclidean time (defining what are now known as D-instantons) were introduced by Michael GreenMichael Green (physicist)
Michael Boris Green FRS is a British physicist and one of the pioneers of string theory. Currently a professor in the Department of Applied Mathematics and Theoretical Physics and a Fellow in Clare Hall at the University of Cambridge in England, he succeeded Stephen Hawking on 1 November 2009...
in 1977 as a means of introducing point-like structure into string theory, in an attempt to construct a string theory of the strong interaction
Strong interaction
In particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
. String compactifications studied by Harvey and Minahan, Ishibashi and Onogi, and Pradisi and Sagnotti in 1987-89 also employed Dirichlet boundary conditions.
The fact that T-duality
T-duality
T-duality is a symmetry of quantum field theories with differing classical descriptions, of which the relationship between small and large distances in various string theories is a special case. Discussion of the subject originated in a paper by T. S. Buscher and was further developed by Martin...
interchanges the usual Neumann boundary conditions with Dirichlet boundary conditions was discovered independently by Horava and by Dai, Leigh, and Polchinski
Joseph Polchinski
Joseph Polchinski is a physicist working on string theory. He graduated from Canyon del Oro High School in Tucson, Arizona in 1971, obtained his B.S. degree from Caltech in 1975, and his Ph.D. from the University of California, Berkeley in 1980 under the supervision of Stanley Mandelstam...
in 1989; this result implies that such boundary conditions must necessarily appear in regions of the moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of any open string theory. The Dai et al. paper also notes that the locus of the Dirichlet boundary conditions is dynamical, and coins the term Dirichlet-brane (D-brane) for the resulting object (this paper also coins orientifold
Orientifold
In theoretical physics orientifold is a generalization of the notion of orbifold, proposed by Augusto Sagnotti in 1987. The novelty is that in the case of string theory the non-trivial element of the orbifold group includes the reversal of the orientation of the string...
for another object that arises under string T-duality). A 1989 paper by Leigh showed that D-brane dynamics are governed by the Dirac-Born-Infeld action. D-instantons were extensively studied by Green in the early 1990s, and were shown by Polchinski in 1994 to produce the e^{-1/g} nonperturbative string effects anticipated by Shenker. In 1995 Polchinski showed that D-branes are the sources of electric and magnetic Ramond-Ramond field
Ramond-Ramond field
In theoretical physics, Ramond–Ramond fields are differential form fields in the 10-dimensional spacetime of type II supergravity theories, which are the classical limits of type II string theory. The ranks of the fields depend on which type II theory is considered...
s that are required by string duality, leading to rapid progress in the nonperturbative understanding of string theory.

