K-theory (physics)
Encyclopedia
In string theory
, the K-theory classification refers to a conjectured application of K-theory
(in abstract algebra
and algebraic topology
) to superstrings, to classify the allowed Ramond-Ramond field
strengths as well as the charges of stable D-branes.
In condensed matter physics
K-theory has also found important applications, specially in the topological classification of topological insulator
s, superconductors and stable Fermi Surfaces .
's realization of arbitrary D-brane configurations as stacks of D9 and anti-D9-branes after tachyon condensation
.
Such stacks of branes are inconsistent in a non-torsion Neveu-Schwarz (NS) 3-form
background, which, as was highlighted by , complicates the extension of the K-theory classification to such cases. suggested a solution to this problem: D-branes are in general classified by a twisted K-theory
, that had earlier been defined by .
one-plane. applied the K-theory classification to derive new consistency conditions for flux compactifications. K-theory has also been used to conjecture a formula for the topologies of T-dual
manifolds by . Recently K-theory has been conjectured to classify the spinors in compactification
s on generalized complex manifolds.
are not quite classified by K-theory. argued that the K-theory classification is incompatible with S-duality
in IIB string theory
.
In addition, if one attempts to classify fluxes on a compact ten-dimensional spacetime, then a complication arises due to the self-duality of the RR fluxes. The duality uses the Hodge star, which depends on the metric and so is continuously valued and in particular is generically irrational. Thus not all of the RR fluxes, which are interpreted as the Chern characters in K-theory, can be rational. However Chern characters are always rational, and so the K-theory classification must be replaced. One needs to choose a half of the fluxes to quantize, or a polarization
in the geometric quantization
-inspired language of Diaconescu, Moore, and Witten and later of . Alternately one may use the K-theory of a 9-dimensional time
slice as has been done by .
, which is type II supergravity
, the Ramond-Ramond field strengths
are differential forms. In the quantum theory the well-definedness of the partition functions of D-branes implies that the RR field strengths obey Dirac quantization conditions when spacetime
is compact
, or when a spatial slice is compact and one considers only the (magnetic) components of the field strength which lie along the spatial directions. This led twentieth century physicists to classify RR field strengths using cohomology
with integral coefficients.
However some authors have argued that the cohomology of spacetime with integral coefficients is too big. For example, in the presence of Neveu-Schwarz H-flux or non-spin cycles some RR fluxes dictate the presence of D-branes. In the former case this is a consequence of the supergravity equation of motion which states that the product of a RR flux with the NS 3-form is a D-brane charge density. Thus the set of topologically distinct RR field strengths that can exist in brane-free configurations is only a subset of the cohomology with integral coefficients.
This subset is still too big, because some of these classes are related by large gauge transformations. In QED there are large gauge transformations which add integral multiples of two pi to Wilson loops. The p-form potentials in type II supergravity theories also enjoy these large gauge transformations, but due to the presence of Chern-Simons terms in the supergravity actions these large gauge transformations transform not only the p-form potentials but also simultaneously the (p+3)-form field strengths. Thus to obtain the space of inequivalent field strengths from the forementioned subset of integral cohomology we must quotient by these large gauge transformations.
The Atiyah-Hirzebruch spectral sequence constructs twisted K-theory, with a twist given by the NS 3-form field strength, as a quotient of a subset of the cohomology
with integral coefficients. In the classical limit, which corresponds to working with rational coefficients, this is precisely the quotient of a subset described above in supergravity. The quantum corrections come from torsion classes and contain mod 2 torsion corrections due to the Freed-Witten anomaly.
Thus twisted K-theory classifies the subset of RR field strengths that can exist in the absence of D-branes quotiented by large gauge transformations. Daniel Freed has attempted to extend this classification to include also the RR potentials using differential K-theory.
, the K-theory classification of D-branes is independent of, and in some ways stronger than, the classification of BPS states. K-theory appears to classify stable D-branes missed by supersymmetry
based classifications.
For example, D-branes with torsion charges, that is with charges in the order N cyclic group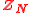
, attract each other and so can never be BPS. In fact, N such branes can decay, whereas no superposition of branes that satisfy a Bogomolny bound may ever decay. However the charge of such branes is conserved modulo N, and this is captured by the K-theory classification but not by a BPS classification. Such torsion branes have been applied, for example, to model Douglas-Shenker strings in supersymmetric U(N) gauge theories
.
has conjectured that, in the absence of a topologically nontrivial NS 3-form flux, all IIB brane configurations can be obtained from stacks of spacefilling D9 and anti D9 branes via tachyon condensation
. The topology of the resulting branes is encoded in the topology of the gauge bundle on the stack of the spacefilling branes. The topology of the gauge bundle of a stack of D9s and anti D9s can be decomposed into a gauge bundle on the D9's and another bundle on the anti D9's. Tachyon condensation transforms such a pair of bundles to another pair in which the same bundle is direct summed with each component in the pair. Thus the tachyon condensation invariant quantity, that is, the charge which is conserved by the tachyon condensation process, is not a pair of bundles but rather the equivalence class of a pair of bundles under direct sums of the same bundle on both sides of the pair. This is precisely the usual construction of topological K-theory
. Thus the gauge bundles on stacks of D9's and anti-D9's are classified by topological K-theory. If Sen's conjecture is right, all D-brane configurations in type IIB are then classified by K-theory. Petr Horava
has extended this conjecture to type IIA using D8-branes.
The central observation is that D-branes are not classified by integral homology because Dp-branes wrapping certain cycles suffer from a Freed-Witten anomaly, which is cancelled by the insertion of D(p-2)-branes and sometimes D(p-4)-branes that end on the afflicted Dp-brane. These inserted branes may either continue to infinity, in which case the composite object has an infinite mass, or else they may end on an anti-Dp-brane, in which case the total Dp-brane charge is zero. In either case, one may wish to remove the anomalous Dp-branes from the spectrum, leaving only a subset of the original integral cohomology.
The inserted branes are unstable. To see this, imagine that they extend in time away (into the past) from the anomalous brane. This corresponds to a process in which the inserted branes decay via a Dp-brane that forms, wraps the forementioned cycle and then disappears. MMS refer to this process as an instanton, although really it need not be instantonic.
The conserved charges are thus the nonanomolous subset quotiented by the unstable insertions. This is precisely the Atiyah-Hirzebruch spectral sequence construction of twisted K-theory as a set.
covariance of type IIB string theory. For example, consider the constraint on the Ramond-Ramond 3-form field strength
G3 in the Atiyah-Hirzebruch spectral sequence (AHSS):
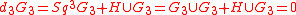
where d3=Sq3+H is the first nontrivial differential in the AHSS, Sq3 is the third Steenrod square and the last equality follows from the fact that the nth Steenrod square acting on any n-form x is x
x.
The above equation is not invariant under S-duality, which exchanges G3 and H. Instead Diaconescu, Moore, and Witten have proposed the following S-duality covariant extension
where P is an unknown characteristic class that depends only on the topology, and in particular not on the fluxes. have found a constraint on P using the E8 gauge theory approach to M-theory pioneered by Diaconescu, Moore, and Witten.
Thus D-branes in IIB are not classified by twisted K-theory after all, but some unknown S-duality-covariant object that inevitably also classifies both fundamental strings and NS5-brane
s.
However the MMS prescription for calculating twisted K-theory is easily S-covariantized, as the Freed-Witten anomalies respect S-duality. Thus the S-covariantized form of the MMS construction may be applied to construct the S-covariantized twisted K-theory, as a set, without knowing having any geometric description for just what this strange covariant object is. This program has been carried out in a number of papers, such as and , and was also applied to the classification of fluxes by . use this approach to prove Diaconescu, Moore, and Witten's conjectured constraint on the 3-fluxes, and they show that there is an additional term equal to the D3-brane charge. shows that the Klebanov-Strassler cascade of Seiberg dualities
consists of a series of S-dual MMS instantons, one for each Seiberg duality. The group,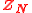
of universality classes of the 
supersymmetric gauge theory
is then shown to agree with the S-dual twisted K-theory and not with the original twisted K-theory.
Some authors have proposed radically different solutions to this puzzle. For example, propose that instead of twisted K-theory, II string theory configurations should be classified by elliptic cohomology
.
, Juan Maldacena, Daniel Freed, and Igor Kriz.
classification of D-branes in 10 dimensions via Ashoke Sen
's conjecture is the original paper "D-branes and K-theory" by Edward Witten
; there is also an extensive review by .
A very comprehensible introduction to the twisted K-theory
classification of conserved D-brane charges on a 9-dimensional timeslice in the presence of Neveu-Schwarz flux is .
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, the K-theory classification refers to a conjectured application of K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
(in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
) to superstrings, to classify the allowed Ramond-Ramond field
Ramond-Ramond field
In theoretical physics, Ramond–Ramond fields are differential form fields in the 10-dimensional spacetime of type II supergravity theories, which are the classical limits of type II string theory. The ranks of the fields depend on which type II theory is considered...
strengths as well as the charges of stable D-branes.
In condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
K-theory has also found important applications, specially in the topological classification of topological insulator
Topological insulator
A topological insulator is a material that behaves as an insulator in its interior or bulk while permitting the movement of charges on its surface....
s, superconductors and stable Fermi Surfaces .
History
This conjecture, applied to D-brane charges, was first proposed by . It was popularized by who demonstrated that in type IIB string theory arises naturally from Ashoke SenAshoke Sen
Ashoke Sen , FRS, is an Indian theoretical physicist. He has made a number of major original contributions to the subject of string theory, including his landmark paper on strong-weak coupling duality or S-duality, which was influential in changing the course of research in the field...
's realization of arbitrary D-brane configurations as stacks of D9 and anti-D9-branes after tachyon condensation
Tachyon condensation
In particle physics, theoretical processes that eliminate or resolve particles or fields into better understood phenomena are called, by extension and metaphor with the macroscopic process, "condensation"...
.
Such stacks of branes are inconsistent in a non-torsion Neveu-Schwarz (NS) 3-form
Kalb-Ramond field
In theoretical physics in general and string theory in particular, the Kalb–Ramond field, also known as the NS-NS B-field, is a quantum field that transforms as a two-form i.e. an antisymmetric tensor field with two indices....
background, which, as was highlighted by , complicates the extension of the K-theory classification to such cases. suggested a solution to this problem: D-branes are in general classified by a twisted K-theory
Twisted K-theory
In mathematics, twisted K-theory is a variation on K-theory, a mathematical theory from the 1950s that spans algebraic topology, abstract algebra and operator theory....
, that had earlier been defined by .
Applications
The K-theory classification of D-branes has had numerous applications. For example, used it to argue that there are eight species of orientifoldOrientifold
In theoretical physics orientifold is a generalization of the notion of orbifold, proposed by Augusto Sagnotti in 1987. The novelty is that in the case of string theory the non-trivial element of the orbifold group includes the reversal of the orientation of the string...
one-plane. applied the K-theory classification to derive new consistency conditions for flux compactifications. K-theory has also been used to conjecture a formula for the topologies of T-dual
T-duality
T-duality is a symmetry of quantum field theories with differing classical descriptions, of which the relationship between small and large distances in various string theories is a special case. Discussion of the subject originated in a paper by T. S. Buscher and was further developed by Martin...
manifolds by . Recently K-theory has been conjectured to classify the spinors in compactification
Compactification (physics)
In physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic....
s on generalized complex manifolds.
Open problems
Despite these successes, RR fluxesRamond-Ramond field
In theoretical physics, Ramond–Ramond fields are differential form fields in the 10-dimensional spacetime of type II supergravity theories, which are the classical limits of type II string theory. The ranks of the fields depend on which type II theory is considered...
are not quite classified by K-theory. argued that the K-theory classification is incompatible with S-duality
S-duality
In theoretical physics, S-duality is an equivalence of two quantum field theories or string theories. An S-duality transformation maps states and vacua with coupling constant g in one theory to states and vacua with coupling constant 1/g in the dual theory...
in IIB string theory
Type II string theory
In theoretical physics, type II string theory is a unified term that includes both type IIA strings and type IIB strings. These account for two of the five consistent superstring theories in ten dimensions. Both theories have the maximal amount of supersymmetry — namely 32 supercharges...
.
In addition, if one attempts to classify fluxes on a compact ten-dimensional spacetime, then a complication arises due to the self-duality of the RR fluxes. The duality uses the Hodge star, which depends on the metric and so is continuously valued and in particular is generically irrational. Thus not all of the RR fluxes, which are interpreted as the Chern characters in K-theory, can be rational. However Chern characters are always rational, and so the K-theory classification must be replaced. One needs to choose a half of the fluxes to quantize, or a polarization
Polarization
Polarization is a property of certain types of waves that describes the orientation of their oscillations. Electromagnetic waves, such as light, and gravitational waves exhibit polarization; acoustic waves in a gas or liquid do not have polarization because the direction of vibration and...
in the geometric quantization
Geometric quantization
In mathematical physics, geometric quantization is a mathematical approach to defining a quantum theory corresponding to a given classical theory. It attempts to carry out quantization, for which there is in general no exact recipe, in such a way that certain analogies between the classical theory...
-inspired language of Diaconescu, Moore, and Witten and later of . Alternately one may use the K-theory of a 9-dimensional time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
slice as has been done by .
K-theory classification of RR fluxes
In the classical limit of type II string theoryType II string theory
In theoretical physics, type II string theory is a unified term that includes both type IIA strings and type IIB strings. These account for two of the five consistent superstring theories in ten dimensions. Both theories have the maximal amount of supersymmetry — namely 32 supercharges...
, which is type II supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
, the Ramond-Ramond field strengths
Ramond-Ramond field
In theoretical physics, Ramond–Ramond fields are differential form fields in the 10-dimensional spacetime of type II supergravity theories, which are the classical limits of type II string theory. The ranks of the fields depend on which type II theory is considered...
are differential forms. In the quantum theory the well-definedness of the partition functions of D-branes implies that the RR field strengths obey Dirac quantization conditions when spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, or when a spatial slice is compact and one considers only the (magnetic) components of the field strength which lie along the spatial directions. This led twentieth century physicists to classify RR field strengths using cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
with integral coefficients.
However some authors have argued that the cohomology of spacetime with integral coefficients is too big. For example, in the presence of Neveu-Schwarz H-flux or non-spin cycles some RR fluxes dictate the presence of D-branes. In the former case this is a consequence of the supergravity equation of motion which states that the product of a RR flux with the NS 3-form is a D-brane charge density. Thus the set of topologically distinct RR field strengths that can exist in brane-free configurations is only a subset of the cohomology with integral coefficients.
This subset is still too big, because some of these classes are related by large gauge transformations. In QED there are large gauge transformations which add integral multiples of two pi to Wilson loops. The p-form potentials in type II supergravity theories also enjoy these large gauge transformations, but due to the presence of Chern-Simons terms in the supergravity actions these large gauge transformations transform not only the p-form potentials but also simultaneously the (p+3)-form field strengths. Thus to obtain the space of inequivalent field strengths from the forementioned subset of integral cohomology we must quotient by these large gauge transformations.
The Atiyah-Hirzebruch spectral sequence constructs twisted K-theory, with a twist given by the NS 3-form field strength, as a quotient of a subset of the cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
with integral coefficients. In the classical limit, which corresponds to working with rational coefficients, this is precisely the quotient of a subset described above in supergravity. The quantum corrections come from torsion classes and contain mod 2 torsion corrections due to the Freed-Witten anomaly.
Thus twisted K-theory classifies the subset of RR field strengths that can exist in the absence of D-branes quotiented by large gauge transformations. Daniel Freed has attempted to extend this classification to include also the RR potentials using differential K-theory.
K-theory classification of D-branes
K-theory classifies D-branes in noncompact spacetimes, intuitively in spacetimes in which we are not concerned about the flux sourced by the brane having nowhere to go. While the K-theory of a 10d spacetime classifies D-branes as subsets of that spacetime, if the spacetime is the product of time and a fixed 9-manifold then K-theory also classifies the conserved D-brane charges on each 9-dimensional spatial slice. While we were required to forget about RR potentials to obtain the K-theory classification of RR field strengths, we are required to forget about RR field strengths to obtain the K-theory classification of D-branes.K-theory charge versus BPS charge
As has been stressed by Petr HořavaPetr Horava
Petr Hořava is a Czech string theorist. He is currently a professor of physics at the University of California, Berkeley, where he frequently teaches courses on quantum field theory and string theory...
, the K-theory classification of D-branes is independent of, and in some ways stronger than, the classification of BPS states. K-theory appears to classify stable D-branes missed by supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
based classifications.
For example, D-branes with torsion charges, that is with charges in the order N cyclic group
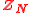, attract each other and so can never be BPS. In fact, N such branes can decay, whereas no superposition of branes that satisfy a Bogomolny bound may ever decay. However the charge of such branes is conserved modulo N, and this is captured by the K-theory classification but not by a BPS classification. Such torsion branes have been applied, for example, to model Douglas-Shenker strings in supersymmetric U(N) gauge theoriesGauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
.
K-theory from tachyon condensation
Ashoke SenAshoke Sen
Ashoke Sen , FRS, is an Indian theoretical physicist. He has made a number of major original contributions to the subject of string theory, including his landmark paper on strong-weak coupling duality or S-duality, which was influential in changing the course of research in the field...
has conjectured that, in the absence of a topologically nontrivial NS 3-form flux, all IIB brane configurations can be obtained from stacks of spacefilling D9 and anti D9 branes via tachyon condensation
Tachyon condensation
In particle physics, theoretical processes that eliminate or resolve particles or fields into better understood phenomena are called, by extension and metaphor with the macroscopic process, "condensation"...
. The topology of the resulting branes is encoded in the topology of the gauge bundle on the stack of the spacefilling branes. The topology of the gauge bundle of a stack of D9s and anti D9s can be decomposed into a gauge bundle on the D9's and another bundle on the anti D9's. Tachyon condensation transforms such a pair of bundles to another pair in which the same bundle is direct summed with each component in the pair. Thus the tachyon condensation invariant quantity, that is, the charge which is conserved by the tachyon condensation process, is not a pair of bundles but rather the equivalence class of a pair of bundles under direct sums of the same bundle on both sides of the pair. This is precisely the usual construction of topological K-theory
Topological K-theory
In mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
. Thus the gauge bundles on stacks of D9's and anti-D9's are classified by topological K-theory. If Sen's conjecture is right, all D-brane configurations in type IIB are then classified by K-theory. Petr Horava
Petr Horava
Petr Hořava is a Czech string theorist. He is currently a professor of physics at the University of California, Berkeley, where he frequently teaches courses on quantum field theory and string theory...
has extended this conjecture to type IIA using D8-branes.
Twisted K-theory from MMS instantons
While the tachyon condensation picture of the K-theory classification classifies D-branes as subsets of a 10-dimensional spacetime with no NS 3-form flux, the Maldacena, Moore, Seiberg picture classifies stable D-branes with finite mass as subsets of a 9-dimensional spatial slice of spacetime.The central observation is that D-branes are not classified by integral homology because Dp-branes wrapping certain cycles suffer from a Freed-Witten anomaly, which is cancelled by the insertion of D(p-2)-branes and sometimes D(p-4)-branes that end on the afflicted Dp-brane. These inserted branes may either continue to infinity, in which case the composite object has an infinite mass, or else they may end on an anti-Dp-brane, in which case the total Dp-brane charge is zero. In either case, one may wish to remove the anomalous Dp-branes from the spectrum, leaving only a subset of the original integral cohomology.
The inserted branes are unstable. To see this, imagine that they extend in time away (into the past) from the anomalous brane. This corresponds to a process in which the inserted branes decay via a Dp-brane that forms, wraps the forementioned cycle and then disappears. MMS refer to this process as an instanton, although really it need not be instantonic.
The conserved charges are thus the nonanomolous subset quotiented by the unstable insertions. This is precisely the Atiyah-Hirzebruch spectral sequence construction of twisted K-theory as a set.
Reconciling twisted K-theory and S-duality
Diaconescu, Moore, and Witten have pointed out that the twisted K-theory classification is not compatible with the S-dualityS-duality
In theoretical physics, S-duality is an equivalence of two quantum field theories or string theories. An S-duality transformation maps states and vacua with coupling constant g in one theory to states and vacua with coupling constant 1/g in the dual theory...
covariance of type IIB string theory. For example, consider the constraint on the Ramond-Ramond 3-form field strength
Ramond-Ramond field
In theoretical physics, Ramond–Ramond fields are differential form fields in the 10-dimensional spacetime of type II supergravity theories, which are the classical limits of type II string theory. The ranks of the fields depend on which type II theory is considered...
G3 in the Atiyah-Hirzebruch spectral sequence (AHSS):
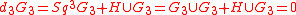
where d3=Sq3+H is the first nontrivial differential in the AHSS, Sq3 is the third Steenrod square and the last equality follows from the fact that the nth Steenrod square acting on any n-form x is x
x.The above equation is not invariant under S-duality, which exchanges G3 and H. Instead Diaconescu, Moore, and Witten have proposed the following S-duality covariant extension
where P is an unknown characteristic class that depends only on the topology, and in particular not on the fluxes. have found a constraint on P using the E8 gauge theory approach to M-theory pioneered by Diaconescu, Moore, and Witten.
Thus D-branes in IIB are not classified by twisted K-theory after all, but some unknown S-duality-covariant object that inevitably also classifies both fundamental strings and NS5-brane
NS5-brane
In theoretical physics, the NS5-brane is a five-dimensional object in string theory that carries a magnetic charge under the B-field, the field under which the fundamental string is electrically charged....
s.
However the MMS prescription for calculating twisted K-theory is easily S-covariantized, as the Freed-Witten anomalies respect S-duality. Thus the S-covariantized form of the MMS construction may be applied to construct the S-covariantized twisted K-theory, as a set, without knowing having any geometric description for just what this strange covariant object is. This program has been carried out in a number of papers, such as and , and was also applied to the classification of fluxes by . use this approach to prove Diaconescu, Moore, and Witten's conjectured constraint on the 3-fluxes, and they show that there is an additional term equal to the D3-brane charge. shows that the Klebanov-Strassler cascade of Seiberg dualities
Seiberg duality
In quantum field theory, Seiberg duality, conjectured by Nathan Seiberg, is an S-duality relating two different supersymmetric QCDs. The two theories are not identical, but they agree at low energies. More precisely under a renormalization group flow they flow to the same IR fixed point, and so...
consists of a series of S-dual MMS instantons, one for each Seiberg duality. The group,
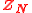of universality classes of the supersymmetric gauge theoryGauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
is then shown to agree with the S-dual twisted K-theory and not with the original twisted K-theory.
Some authors have proposed radically different solutions to this puzzle. For example, propose that instead of twisted K-theory, II string theory configurations should be classified by elliptic cohomology
Elliptic cohomology
In mathematics, elliptic cohomology is a cohomology theory in the sense of algebraic topology. It is related to elliptic curves and modular forms.-History and motivation:Historically, elliptic cohomology arose from the study of elliptic genera...
.
Researchers
Prominent researchers in this area include Peter Bouwknegt, Angel Uranga, Emanuel Diaconescu, Gregory Moore, Anton Kapustin, Jonathan Rosenberg, Ruben Minasian, Amihay Hanany, Hisham Sati, Nathan SeibergNathan Seiberg
Nathan "Nati" Seiberg is an Israeli American theoretical physicist who works on string theory. He was recipient of a 1996 MacArthur Fellowship and the Dannie Heineman Prize for Mathematical Physics in 1998. He is currently a professor at the Institute for Advanced Study in Princeton, New Jersey, USA...
, Juan Maldacena, Daniel Freed, and Igor Kriz.
Further reading
An excellent introduction to the K-theoryK-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
classification of D-branes in 10 dimensions via Ashoke Sen
Ashoke Sen
Ashoke Sen , FRS, is an Indian theoretical physicist. He has made a number of major original contributions to the subject of string theory, including his landmark paper on strong-weak coupling duality or S-duality, which was influential in changing the course of research in the field...
's conjecture is the original paper "D-branes and K-theory" by Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
; there is also an extensive review by .
A very comprehensible introduction to the twisted K-theory
Twisted K-theory
In mathematics, twisted K-theory is a variation on K-theory, a mathematical theory from the 1950s that spans algebraic topology, abstract algebra and operator theory....
classification of conserved D-brane charges on a 9-dimensional timeslice in the presence of Neveu-Schwarz flux is .