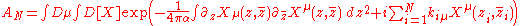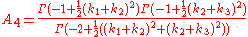Superstring theory
Encyclopedia
Superstring theory is an attempt to explain all
of the particles
and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric
strings. Superstring theory is a shorthand for supersymmetric string theory because unlike bosonic string theory
, it is the version of string theory
that incorporates fermions and supersymmetry.
is harmonizing the theory of general relativity
, which describes gravitation and applies to large-scale structures (star
s, galaxies, super clusters), with quantum mechanics
, which describes the other three fundamental forces acting on the atomic scale.
The development of a quantum field theory
of a force invariably results in infinite (and therefore useless) probabilities. Physicists have developed mathematical techniques (renormalization
) to eliminate these infinities which work for three of the four fundamental forces – electromagnetic, strong nuclear
and weak nuclear
forces – but not for gravity. The development of a quantum theory of gravity must therefore come about by different means than those used for the other forces.
(about 10−33 cm) which vibrate at resonant
frequencies. Every string, in theory, has a unique resonance, or harmonic. Different harmonics determine different fundamental forces. The tension in a string is on the order of the Planck force
(1044 newtons). The graviton
(the proposed messenger particle of the gravitational force), for example, is predicted by the theory to be a string with wave amplitude zero. Another key insight provided by the theory is that no measurable differences can be detected between strings that wrap around dimensions smaller than themselves and those that move along larger dimensions (i.e., effects in a dimension of size R equal those whose size is 1/R). Singularities
are avoided because the observed consequences of "Big Crunch
es" never reach zero size. In fact, should the universe begin a "big crunch" sort of process, string theory dictates that the universe could never be smaller than the size of a string, at which point it would actually begin expanding.
Our physical space is observed to have only three large dimension
s and—taken together with duration as the fourth dimension—a physical theory must take this into account. However, nothing prevents a theory from including more than 4 dimensions. In the case of string theory
, consistency
requires spacetime
to have 10 (3+1+6) dimensions. The conflict between observation and theory is resolved by making the unobserved dimensions compactified
.
Our minds have difficulty visualizing higher dimensions because we can only move in three spatial dimensions. One way of dealing with this limitation is not to try to visualize higher dimensions at all, but just to think of them as extra numbers in the equations that describe the way the world works. This opens the question of whether these 'extra numbers' can be investigated directly in any experiment (which must show different results in 1, 2, or 2 + 1 dimensions to a human scientist). This, in turn, raises the question of whether models that rely on such abstract modelling (and potentially impossibly huge experimental apparatuses) can be considered scientific. Six-dimensional Calabi–Yau shapes can account for the additional dimensions required by superstring theory. The theory states that every point in space (or whatever we had previously considered a point) is in fact a very small manifold
where each extra dimension has a size on the order of the Planck length.
Superstring theory is not the first theory to propose extra spatial dimensions; the Kaluza-Klein theory had done so previously. Modern string theory relies on the mathematics of folds, knots, and topology
, which were largely developed after Kaluza and Klein, and has made physical theories relying on extra dimensions much more credible.
. Unfortunately, however, to this date this remains a conjecture
.
The five consistent superstring theories are:
Chiral gauge theories
can be inconsistent due to anomalies
. This happens when certain one-loop Feynman diagram
s cause a quantum mechanical breakdown of the gauge symmetry. The anomalies were canceled out via the Green–Schwarz mechanism.
Please note that the number of superstring theories given above is only a high-level classification; the actual number of mathematically distinct theories which are compatible with observation and would therefore have to be examined to find the one that correctly describes nature is currently believed to be at least 10500 (a one with five hundred zeroes). This has given rise to the concern that superstring theories, despite the alluring simplicity of their basic principles, are, in fact, not simple at all, and according to the principle of Occam's razor
perhaps alternative physical theories going beyond the Standard Model
should be explored. This is aggravated by the fact that it is exceedingly hard to make predictions from any superstring theory which can be falsified by experiment, and in fact no current superstring theory makes any falsifiable prediction.
General relativity
typically deals with situations involving large mass objects in fairly large regions of spacetime
whereas quantum mechanics
is generally reserved for scenarios at the atomic scale (small spacetime regions). The two are very rarely used together, and the most common case in which they are combined is in the study of black hole
s. Having "peak density", or the maximum amount of matter possible in a space, and very small area, the two must be used in synchrony in order to predict conditions in such places; yet, when used together, the equations fall apart, spitting out impossible answers, such as imaginary distances and less than one dimension.
The major problem with their congruence is that, at Planck scale
(a fundamental small unit of length) lengths, general relativity predicts a smooth, flowing surface, while quantum mechanics predicts a random, warped surface, neither of which are anywhere near compatible. Superstring theory resolves this issue, replacing the classical idea of point particles with loops. These loops have an average diameter of the Planck length, with extremely small variances, which completely ignores the quantum mechanical predictions of Planck-scale length dimensional warping.
the topology change must only occur at a single point. If C represents a closed string and O an open string, then the five interactions are OOO, CCC, OOC, OCO and COO.
All open superstring theories also contain closed superstrings since closed superstrings can be seen from the fifth interaction, and they are unavoidable. Although all these interactions are possible, in practice the most used superstring model is the closed heterotic E8xE8 superstring which only has closed strings and so only the second interaction (CCC) is needed.
s, with momentum ki which connect to a string world surface at the surface points zi. It is given by the following functional integral which integrates (sums) over all possible embeddings of this 2D surface in 27 dimensions:
The functional integral can be done because it is a Gaussian to become:
This is integrated over the various points zi. Special care must be taken because two parts of this complex region may represent the same point on the 2D surface and you don't want to integrate over them twice. Also you need to make sure you are not integrating multiple times over different parameterizations of the surface. When this is taken into account it can be used to calculate the 4-point scattering amplitude (the 3-point amplitude is simply a delta function):
Which is a beta function. It was this beta function which was apparently found before full string theory was developed. With superstrings the equations contain not only the 10D space-time coordinates X but also the Grassmann coordinates θ. Since there are various ways this can be done this leads to different string theories.
When integrating over surfaces such as the torus, we end up with equations in terms of theta functions and elliptic functions such as the Dedekind eta function
. This is smooth everywhere, which it has to be to make physical sense, only when raised to the 24th power. This is the origin of needing 26 dimensions of space-time for bosonic string theory. The extra two dimensions arise as degrees of freedom of the string surface.
In type I open string theory, the ends of open strings are always attached to D-brane surfaces. A string theory with more gauge fields such as SU(2) gauge fields would then correspond to the compactification of some higher dimensional theory above 11 dimensions which is not thought to be possible to date.
The heterotic superstrings come in two types SO(32) and E8×E8 as indicated above and the type I superstrings include open strings.
the functional integrals are very difficult to solve and so this has confounded the top theoretical physicists. Edward Witten
has popularised the concept of a theory in 11 dimensions M-Theory involving membranes interpolating from the known symmetries of superstring theory. It may turn out that there exist membrane models or other non-membrane models in higher dimensions which may become acceptable when new unknown symmetries of nature are found, such as noncommutative geometry for example. It is thought, however, that 16 is probably the maximum since O(16) is a maximal subgroup of E8 the largest exceptional lie group and also is more than large enough to contain the Standard Model
.
Quartic integrals of the non-functional kind are easier to solve so there is hope for the future. This is the series solution which is always convergent when a is non-zero and negative:
In the case of membranes the series would correspond to sums of various membrane interactions that are not seen in string theory.
currently restrict the spinors to have 32-components which limits the number of dimensions to 11 (or 12 if you include two time dimensions.) Some commentators (e.g. John Baez et al.) have speculated that the exceptional lie groups E6, E7 and E8 having maximum orthogonal subgroups O(10), O(12) and O(16) may be related to theories in 10, 12 and 16 dimensions; 10 dimensions corresponding to string theory and the 12 and 16 dimensional theories being yet undiscovered but would be theories based on 3-branes and 7-branes respectively. However this is a minority view within the string community. Since E7 is in some sense F4 quaternified and E8 is F4 octonified, then the 12 and 16 dimensional theories, if they did exist, may involve the noncommutative geometry
based on the quaternions and octonions respectively. From the above discussion, it can be seen that physicists have many ideas for extending superstring theory beyond the current 10 dimensional theory, but so far none have been successful.
have been E10 and E11 and their supersymmetric extensions.
Theory of everything
A theory of everything is a putative theory of theoretical physics that fully explains and links together all known physical phenomena, and predicts the outcome of any experiment that could be carried out in principle....
of the particles
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
strings. Superstring theory is a shorthand for supersymmetric string theory because unlike bosonic string theory
Bosonic string theory
Bosonic string theory is the original version of string theory, developed in the late 1960s.In the early 1970s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory became the real focus...
, it is the version of string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
that incorporates fermions and supersymmetry.
Background
The deepest problem in theoretical physicsTheoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
is harmonizing the theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, which describes gravitation and applies to large-scale structures (star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s, galaxies, super clusters), with quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, which describes the other three fundamental forces acting on the atomic scale.
The development of a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
of a force invariably results in infinite (and therefore useless) probabilities. Physicists have developed mathematical techniques (renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
) to eliminate these infinities which work for three of the four fundamental forces – electromagnetic, strong nuclear
Strong interaction
In particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
and weak nuclear
Weak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
forces – but not for gravity. The development of a quantum theory of gravity must therefore come about by different means than those used for the other forces.
Basic idea
The basic idea is that the fundamental constituents of reality are strings of the Planck lengthPlanck units
In physics, Planck units are physical units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify...
(about 10−33 cm) which vibrate at resonant
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
frequencies. Every string, in theory, has a unique resonance, or harmonic. Different harmonics determine different fundamental forces. The tension in a string is on the order of the Planck force
Planck force
Planck force is the derived unit of force resulting from the definition of the base Planck units for time, length, and mass. It is equal to the natural unit of momentum divided by the natural unit of time....
(1044 newtons). The graviton
Graviton
In physics, the graviton is a hypothetical elementary particle that mediates the force of gravitation in the framework of quantum field theory. If it exists, the graviton must be massless and must have a spin of 2...
(the proposed messenger particle of the gravitational force), for example, is predicted by the theory to be a string with wave amplitude zero. Another key insight provided by the theory is that no measurable differences can be detected between strings that wrap around dimensions smaller than themselves and those that move along larger dimensions (i.e., effects in a dimension of size R equal those whose size is 1/R). Singularities
Gravitational singularity
A gravitational singularity or spacetime singularity is a location where the quantities that are used to measure the gravitational field become infinite in a way that does not depend on the coordinate system...
are avoided because the observed consequences of "Big Crunch
Big Crunch
In physical cosmology, the Big Crunch is one possible scenario for the ultimate fate of the universe, in which the metric expansion of space eventually reverses and the universe recollapses, ultimately ending as a black hole singularity.- Overview :...
es" never reach zero size. In fact, should the universe begin a "big crunch" sort of process, string theory dictates that the universe could never be smaller than the size of a string, at which point it would actually begin expanding.
Extra dimensions
- See also: Why does consistency require 10 dimensions?
Our physical space is observed to have only three large dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s and—taken together with duration as the fourth dimension—a physical theory must take this into account. However, nothing prevents a theory from including more than 4 dimensions. In the case of string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, consistency
Consistency
Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...
requires spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
to have 10 (3+1+6) dimensions. The conflict between observation and theory is resolved by making the unobserved dimensions compactified
Compactification (physics)
In physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic....
.
Our minds have difficulty visualizing higher dimensions because we can only move in three spatial dimensions. One way of dealing with this limitation is not to try to visualize higher dimensions at all, but just to think of them as extra numbers in the equations that describe the way the world works. This opens the question of whether these 'extra numbers' can be investigated directly in any experiment (which must show different results in 1, 2, or 2 + 1 dimensions to a human scientist). This, in turn, raises the question of whether models that rely on such abstract modelling (and potentially impossibly huge experimental apparatuses) can be considered scientific. Six-dimensional Calabi–Yau shapes can account for the additional dimensions required by superstring theory. The theory states that every point in space (or whatever we had previously considered a point) is in fact a very small manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
where each extra dimension has a size on the order of the Planck length.
Superstring theory is not the first theory to propose extra spatial dimensions; the Kaluza-Klein theory had done so previously. Modern string theory relies on the mathematics of folds, knots, and topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, which were largely developed after Kaluza and Klein, and has made physical theories relying on extra dimensions much more credible.
Number of superstring theories
Theoretical physicists were troubled by the existence of five separate string theories. A possible solution for this dilemma was suggested at the beginning of what is called the second superstring revolution in the 1990s, which suggests that the five string theories might be different limits of a single underlying theory, called M-theoryM-theory
In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
. Unfortunately, however, to this date this remains a conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
.
| String theories | |||||||
|---|---|---|---|---|---|---|---|
| Type | Spacetime dimensions | SUSY generators | chiral | open strings? | heterotic compactification? | gauge group | tachyon |
| Bosonic (closed) | 26 | N = 0 | no | no | no | none | yes |
| Bosonic (open) | 26 | N = 0 | no | yes | no | U(1) | yes |
| I | 10 | N = (1,0) | yes | yes | no | SO(32) | no |
| IIA | 10 | N = (1,1) | no | no | no | U(1) | no |
| IIB | 10 | N = (2,0) | yes | no | no | none | no |
| HO | 10 | N = (1,0) | yes | no | yes | SO(32) | no |
| HE | 10 | N = (1,0) | yes | no | yes | 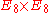 |
no |
| M-theory | 11 | N = 1 | no | no | no | none | no |
The five consistent superstring theories are:
- The type I string has one supersymmetry in the ten-dimensional sense (16 supercharges). This theory is special in the sense that it is based on unoriented open and closed strings, while the rest are based on oriented closed strings.
- The type II string theories have two supersymmetries in the ten-dimensional sense (32 supercharges). There are actually two kinds of type II strings called type IIA and type IIB. They differ mainly in the fact that the IIA theory is non-chiralChirality (physics)A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
(parity conserving) while the IIB theory is chiral (parity violating). - The heterotic stringHeterotic stringIn physics, a heterotic string is a peculiar mixture of the bosonic string and the superstring...
theories are based on a peculiar hybrid of a type I superstring and a bosonic string. There are two kinds of heterotic strings differing in their ten-dimensional gauge groups: the heterotic E8×E8E8 (mathematics)In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
string and the heterotic SO(32) string. (The name heterotic SO(32) is slightly inaccurate since among the SO(32) Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, string theory singles out a quotient Spin(32)/Z2 that is not equivalent to SO(32).)
Chiral gauge theories
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
can be inconsistent due to anomalies
Anomaly (physics)
In quantum physics an anomaly or quantum anomaly is the failure of a symmetry of a theory's classical action to be a symmetry of any regularization of the full quantum theory. In classical physics an anomaly is the failure of a symmetry to be restored in the limit in which the symmetry-breaking...
. This happens when certain one-loop Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s cause a quantum mechanical breakdown of the gauge symmetry. The anomalies were canceled out via the Green–Schwarz mechanism.
Please note that the number of superstring theories given above is only a high-level classification; the actual number of mathematically distinct theories which are compatible with observation and would therefore have to be examined to find the one that correctly describes nature is currently believed to be at least 10500 (a one with five hundred zeroes). This has given rise to the concern that superstring theories, despite the alluring simplicity of their basic principles, are, in fact, not simple at all, and according to the principle of Occam's razor
Occam's razor
Occam's razor, also known as Ockham's razor, and sometimes expressed in Latin as lex parsimoniae , is a principle that generally recommends from among competing hypotheses selecting the one that makes the fewest new assumptions.-Overview:The principle is often summarized as "simpler explanations...
perhaps alternative physical theories going beyond the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
should be explored. This is aggravated by the fact that it is exceedingly hard to make predictions from any superstring theory which can be falsified by experiment, and in fact no current superstring theory makes any falsifiable prediction.
Integrating general relativity and quantum mechanics
General relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
typically deals with situations involving large mass objects in fairly large regions of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
whereas quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
is generally reserved for scenarios at the atomic scale (small spacetime regions). The two are very rarely used together, and the most common case in which they are combined is in the study of black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s. Having "peak density", or the maximum amount of matter possible in a space, and very small area, the two must be used in synchrony in order to predict conditions in such places; yet, when used together, the equations fall apart, spitting out impossible answers, such as imaginary distances and less than one dimension.
The major problem with their congruence is that, at Planck scale
Planck scale
In particle physics and physical cosmology, the Planck scale is an energy scale around 1.22 × 1019 GeV at which quantum effects of gravity become strong...
(a fundamental small unit of length) lengths, general relativity predicts a smooth, flowing surface, while quantum mechanics predicts a random, warped surface, neither of which are anywhere near compatible. Superstring theory resolves this issue, replacing the classical idea of point particles with loops. These loops have an average diameter of the Planck length, with extremely small variances, which completely ignores the quantum mechanical predictions of Planck-scale length dimensional warping.
The five superstring interactions
There are five ways open and closed strings can interact. An interaction in superstring theory is a topology changing event. Since superstring theory has to be a local theory to obey causalityCausality
Causality is the relationship between an event and a second event , where the second event is understood as a consequence of the first....
the topology change must only occur at a single point. If C represents a closed string and O an open string, then the five interactions are OOO, CCC, OOC, OCO and COO.
All open superstring theories also contain closed superstrings since closed superstrings can be seen from the fifth interaction, and they are unavoidable. Although all these interactions are possible, in practice the most used superstring model is the closed heterotic E8xE8 superstring which only has closed strings and so only the second interaction (CCC) is needed.
The mathematics
The single most important equation in (first quantized bosonic) string theory is the N-point scattering amplitude. This treats the incoming and outgoing strings as points, which in string theory are tachyonTachyon
A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph...
s, with momentum ki which connect to a string world surface at the surface points zi. It is given by the following functional integral which integrates (sums) over all possible embeddings of this 2D surface in 27 dimensions:
The functional integral can be done because it is a Gaussian to become:
This is integrated over the various points zi. Special care must be taken because two parts of this complex region may represent the same point on the 2D surface and you don't want to integrate over them twice. Also you need to make sure you are not integrating multiple times over different parameterizations of the surface. When this is taken into account it can be used to calculate the 4-point scattering amplitude (the 3-point amplitude is simply a delta function):
Which is a beta function. It was this beta function which was apparently found before full string theory was developed. With superstrings the equations contain not only the 10D space-time coordinates X but also the Grassmann coordinates θ. Since there are various ways this can be done this leads to different string theories.
When integrating over surfaces such as the torus, we end up with equations in terms of theta functions and elliptic functions such as the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
. This is smooth everywhere, which it has to be to make physical sense, only when raised to the 24th power. This is the origin of needing 26 dimensions of space-time for bosonic string theory. The extra two dimensions arise as degrees of freedom of the string surface.
D-branes
D-branes are membrane-like objects in 10D string theory. They can be thought of as occurring as a result of a Kaluza-Klein compactification of 11D M-Theory which contains membranes. Because compactification of a geometric theory produces extra vector fields the D-branes can be included in the action by adding an extra U(1) vector field to the string action.In type I open string theory, the ends of open strings are always attached to D-brane surfaces. A string theory with more gauge fields such as SU(2) gauge fields would then correspond to the compactification of some higher dimensional theory above 11 dimensions which is not thought to be possible to date.
Why five superstring theories?
For a 10 dimensional supersymmetric theory we are allowed a 32-component Majorana spinor. This can be decomposed into a pair of 16-component Majorana-Weyl (chiral) spinors. There are then various ways to construct an invariant depending on whether these two spinors have the same or opposite chiralities:| Superstring model | Invariant |
|---|---|
| Heterotic | 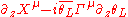 |
| IIA |  |
| IIB | 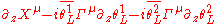 |
The heterotic superstrings come in two types SO(32) and E8×E8 as indicated above and the type I superstrings include open strings.
Beyond superstring theory
It is commonly believed that the five superstring theories are approximated to a theory in higher dimensions possibly involving membranes. Unfortunately because the action for this involves quartic terms and higher so is not GaussianGAUSSIAN
Gaussian is a computational chemistry software program initially released in 1970 by John Pople and his research group at Carnegie-Mellon University as Gaussian 70. It has been continuously updated since then...
the functional integrals are very difficult to solve and so this has confounded the top theoretical physicists. Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
has popularised the concept of a theory in 11 dimensions M-Theory involving membranes interpolating from the known symmetries of superstring theory. It may turn out that there exist membrane models or other non-membrane models in higher dimensions which may become acceptable when new unknown symmetries of nature are found, such as noncommutative geometry for example. It is thought, however, that 16 is probably the maximum since O(16) is a maximal subgroup of E8 the largest exceptional lie group and also is more than large enough to contain the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
.
Quartic integrals of the non-functional kind are easier to solve so there is hope for the future. This is the series solution which is always convergent when a is non-zero and negative:
In the case of membranes the series would correspond to sums of various membrane interactions that are not seen in string theory.
Compactification
Investigating theories of higher dimensions often involves looking at the 10 dimensional superstring theory and interpreting some of the more obscure results in terms of compactified dimensions. For example D-branes are seen as compactified membranes from 11D M-Theory. Theories of higher dimensions such as 12D F-theory and beyond will produce other effects such as gauge terms higher than U(1). The components of the extra vector fields (A) in the D-brane actions can be thought of as extra coordinates (X) in disguise. However, the known symmetries including supersymmetrySupersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
currently restrict the spinors to have 32-components which limits the number of dimensions to 11 (or 12 if you include two time dimensions.) Some commentators (e.g. John Baez et al.) have speculated that the exceptional lie groups E6, E7 and E8 having maximum orthogonal subgroups O(10), O(12) and O(16) may be related to theories in 10, 12 and 16 dimensions; 10 dimensions corresponding to string theory and the 12 and 16 dimensional theories being yet undiscovered but would be theories based on 3-branes and 7-branes respectively. However this is a minority view within the string community. Since E7 is in some sense F4 quaternified and E8 is F4 octonified, then the 12 and 16 dimensional theories, if they did exist, may involve the noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
based on the quaternions and octonions respectively. From the above discussion, it can be seen that physicists have many ideas for extending superstring theory beyond the current 10 dimensional theory, but so far none have been successful.
Kac–Moody algebras
Since strings can have an infinite number of modes, the symmetry used to describe string theory is based on infinite dimensional Lie algebras. Some Kac–Moody algebras that have been considered as symmetries for M-TheoryM-theory
In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
have been E10 and E11 and their supersymmetric extensions.
See also
- AdS/CFT
- Grand unification theoryGrand unification theoryThe term Grand Unified Theory, often abbreviated as GUT, refers to any of several similar candidate models in particle physics in which at high-energy, the three gauge interactions of the Standard Model which define the electromagnetic, weak, and strong interactions, are merged into one single...
- Large Hadron ColliderLarge Hadron ColliderThe Large Hadron Collider is the world's largest and highest-energy particle accelerator. It is expected to address some of the most fundamental questions of physics, advancing the understanding of the deepest laws of nature....
- List of string theory topics
- Quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
- String field theoryString field theoryString field theory is a formalism in string theory in which the dynamics of relativistic strings is reformulated in the language of quantum field theory...
General references
- Wellcome Collection video on superstring theory
- The Official Superstring theory website: http://superstringtheory.com/index.html