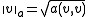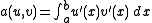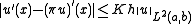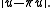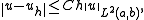
Céa's lemma
Encyclopedia
Céa's lemma is a lemma
in mathematics
. It is an important tool for proving error estimates for the finite element method
applied to elliptic
partial differential equation
s.
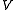 be a real
be a real
Hilbert space
with the norm
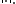 Let
Let 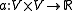 be a bilinear form with the properties
be a bilinear form with the properties
Let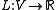 be a bounded linear operator. Consider the problem of finding an element
be a bounded linear operator. Consider the problem of finding an element  in
in 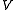 such that
such that
Consider the same problem on a finite-dimensional subspace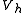 of
of 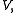 so,
so,  in
in 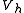 satisfies
satisfies
By the Lax–Milgram theorem, each of these problems has exactly one solution. Céa's lemma states that
That is to say, the subspace solution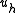 is "the best" approximation of
is "the best" approximation of  in
in 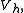 up to
up to
the constant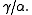
The proof is straightforward
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. It is an important tool for proving error estimates for the finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
applied to elliptic
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s.
Lemma statement
Let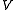 be a real
be a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
with the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
 Let
Let 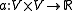 be a bilinear form with the properties
be a bilinear form with the properties-
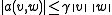 for some constant
for some constant 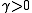 and all
and all  in
in  (continuityContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
(continuityContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
)
-
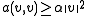 for some constant
for some constant 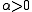 and all
and all  in
in 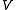 (coercivity or
(coercivity or 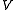 -ellipticity).
-ellipticity).
Let
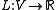 be a bounded linear operator. Consider the problem of finding an element
be a bounded linear operator. Consider the problem of finding an element  in
in 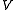 such that
such that-
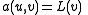 for all
for all  in
in 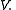
Consider the same problem on a finite-dimensional subspace
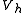 of
of 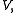 so,
so,  in
in 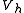 satisfies
satisfies-
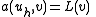 for all
for all  in
in 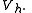
By the Lax–Milgram theorem, each of these problems has exactly one solution. Céa's lemma states that
-
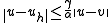 for all
for all  in
in 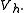
That is to say, the subspace solution
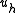 is "the best" approximation of
is "the best" approximation of  in
in 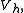 up to
up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
the constant
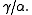
The proof is straightforward
-
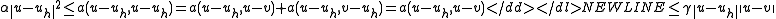 for all
for all  in
in 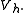
We used the -orthogonality of
-orthogonality of 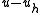 and
and 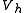
-
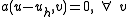 in
in 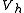
which follows directly from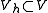
-
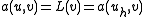 for all
for all  in
in 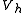 .
.
Note: Céa's lemma holds on complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Hilbert spaces also, one then uses a sesquilinear formSesquilinear formIn mathematics, a sesquilinear form on a complex vector space V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix sesqui- meaning "one and a half"...
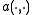 instead of a bilinear one. The coercivity assumption then becomes
instead of a bilinear one. The coercivity assumption then becomes 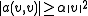 for all
for all  in
in 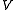 (notice the absolute value sign around
(notice the absolute value sign around 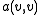 ).
).
Error estimate in the energy norm
In many applications, the bilinear form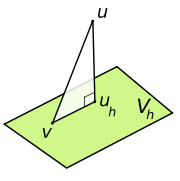
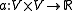 is symmetric, so
is symmetric, so
-
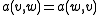 for all
for all 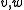 in
in 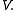
This, together with the above properties of this form, implies that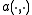 is an inner product on
is an inner product on 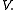 The resulting norm
The resulting norm
is called the energy norm, since it corresponds to a physical energy in many problems. This norm is equivalent to the original norm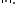
Using the -orthogonality of
-orthogonality of 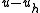 and
and 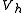 and the Cauchy–Schwarz inequalityCauchy–Schwarz inequalityIn mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
and the Cauchy–Schwarz inequalityCauchy–Schwarz inequalityIn mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
-
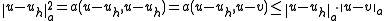 for all
for all  in
in 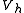 .
.
Hence, in the energy norm, the inequality in Céa's lemma becomes
-
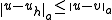 for all
for all  in
in 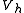
(notice that the constant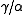 on the right-hand side is no longer present).
on the right-hand side is no longer present).
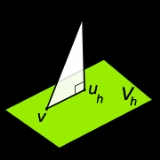
This states that the subspace solution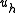 is the best approximation to the full-space solution
is the best approximation to the full-space solution  in respect to the energy norm. Geometrically, this means that
in respect to the energy norm. Geometrically, this means that 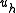 is the projectionProjection (linear algebra)In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
is the projectionProjection (linear algebra)In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
of the solution onto the subspace
onto the subspace 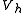 in respect to the inner product
in respect to the inner product 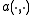 (see the picture on the right).
(see the picture on the right).
Using this result, one can also derive a sharper estimate in the norm . Since
. Since
-
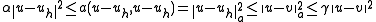 for all
for all  in
in 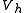 ,
,
it follows that-
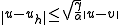 for all
for all  in
in 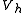 .
.
An application of Céa's lemma
We will apply Céa's lemma to estimate the error of calculating the solution to an elliptic differential equation by the finite element methodFinite element methodThe finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
.
Consider the problem of finding a function
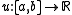 satisfying the conditions
satisfying the conditions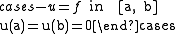
where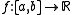 is a given continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
is a given continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
.
Physically, the solution to this two-point boundary value problemBoundary value problemIn mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
to this two-point boundary value problemBoundary value problemIn mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
represents the shape taken by a stringRopeA rope is a length of fibres, twisted or braided together to improve strength for pulling and connecting. It has tensile strength but is too flexible to provide compressive strength...
under the influence of a force such that at every point between
between  and
and 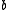 the force densityForce densityIn fluid mechanics, the force density is the negative gradient of pressure. It has the physical dimensions of force per unit volume. Force density is a vector field representing the flux density of the hydrostatic force within the bulk of a fluid...
the force densityForce densityIn fluid mechanics, the force density is the negative gradient of pressure. It has the physical dimensions of force per unit volume. Force density is a vector field representing the flux density of the hydrostatic force within the bulk of a fluid...
is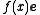 (where
(where  is a unit vector pointing vertically, while the endpoints of the string are on a horizontal line, see the picture on the right). For example, that force may be the gravity, when
is a unit vector pointing vertically, while the endpoints of the string are on a horizontal line, see the picture on the right). For example, that force may be the gravity, when 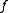 is a constant function (since the gravitational force is the same at all points).
is a constant function (since the gravitational force is the same at all points).
Let the Hilbert space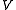 be the Sobolev spaceSobolev spaceIn mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
be the Sobolev spaceSobolev spaceIn mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
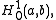 which is the space of all square integrable functions
which is the space of all square integrable functions  defined on
defined on 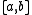 that have a weak derivativeWeak derivativeIn mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
that have a weak derivativeWeak derivativeIn mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
on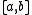 with
with 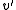 also being square integrable, and
also being square integrable, and  satisfies the conditions
satisfies the conditions 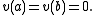 The inner product on this space is
The inner product on this space is
-
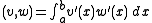 for all
for all  and
and 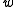 in
in 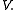
After multiplying the original boundary value problem by in this space and performing an integration by partsIntegration by partsIn calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
in this space and performing an integration by partsIntegration by partsIn calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
, one obtains the equivalent problem
-
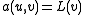 for all
for all  in
in 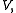
with
(here the bilinear form is given by the same expression as the inner product, this is not always the case), and
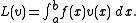
It can be shown that the bilinear form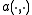 and the operator
and the operator 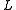 satisfy the assumptions of Céa's lemma.
satisfy the assumptions of Céa's lemma.
In order to determine a finite-dimensional subspace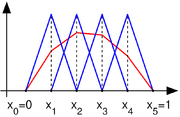
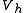 of
of 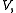 consider a partitionPartition of an intervalIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
consider a partitionPartition of an intervalIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
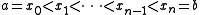
of the interval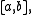 and let
and let 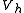 be the space of all continuous functions that are affine on each subinterval in the partition (such functions are called piecewise-linear). In addition, assume that any function in
be the space of all continuous functions that are affine on each subinterval in the partition (such functions are called piecewise-linear). In addition, assume that any function in 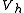 takes the value 0 at the endpoints of
takes the value 0 at the endpoints of  It follows that
It follows that 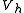 is a vector subspace of
is a vector subspace of 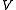 whose dimension is
whose dimension is  (the number of points in the partition that are not endpoints).
(the number of points in the partition that are not endpoints).
Let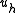 be the solution to the subspace problem
be the solution to the subspace problem
-
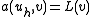 for all
for all  in
in 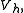
so one can think of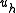 as of a piecewise-linear approximation to the exact solution
as of a piecewise-linear approximation to the exact solution 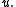 By Céa's lemma, there exists a constant
By Céa's lemma, there exists a constant 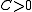 dependent only on the bilinear form
dependent only on the bilinear form 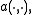 such that
such that
-
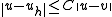 for all
for all  in
in 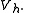
To explicitly calculate the error between and
and 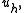 consider the function
consider the function 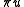 in
in 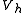 that has the same values as
that has the same values as  at the nodes of the partition (so
at the nodes of the partition (so 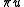 is obtained by linear interpolation on each interval
is obtained by linear interpolation on each interval 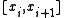 from the values of
from the values of  at interval's endpoints). It can be shown using Taylor's theoremTaylor's theoremIn calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
at interval's endpoints). It can be shown using Taylor's theoremTaylor's theoremIn calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
that there exists a constant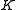 that depends only on the endpoints
that depends only on the endpoints  and
and 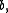 such that
such that
for all in
in 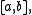 where
where 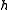 is the largest length of the subintervals
is the largest length of the subintervals 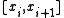 in the partition, and the norm on the right-hand side is the L2 normLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
in the partition, and the norm on the right-hand side is the L2 normLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
.
This inequality then yields an estimate for the error
Then, by substituting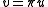 in Céa's lemma it follows that
in Céa's lemma it follows that
where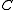 is a different constant from the above (it depends only on the bilinear form, which implicitly depends on the interval
is a different constant from the above (it depends only on the bilinear form, which implicitly depends on the interval 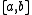 ).
).
This result is of a fundamental importance, as it states that the finite element method can be used to approximately calculate the solution of our problem, and that the error in the computed solution decreases proportionately to the partition size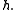 Céa's lemma can be applied along the same lines to derive error estimates for finite element problems in higher dimensions (here the domain of
Céa's lemma can be applied along the same lines to derive error estimates for finite element problems in higher dimensions (here the domain of  was in one dimension), and while using higher order polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
was in one dimension), and while using higher order polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s for the subspace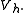
-