Cyclic homology
Encyclopedia
In homological algebra
, cyclic homology and cyclic cohomology are (co)homology theories for associative algebra
s introduced by Alain Connes
around 1980, which play an important role in his noncommutative geometry
. They were independently discovered by Boris Tsygan and studied by Connes, Karoubi, Feigin-Tsygan, Loday, Quillen, and others.
zero, denoted
proceeded by the means of an explicit chain complex
related to the Hochschild homology complex
of A. Connes later found a more categorical approach to cyclic homology using a notion of cyclic object in an abelian category
, which is analogous to the notion of simplicial object. In this way, cyclic homology (and cohomology) may be interpreted as a derived functor
, which can be explicitly computed by the means of the Connes bicomplex.
One of the striking features of cyclic homology is the existence of a long exact sequence connecting
Hochschild and cyclic homology. This long exact sequence is referred to as the periodicity sequence.
. In particular, if the variety V=Spec A is smooth, cyclic cohomology of A are expressed in terms of the de Rham cohomology
of V as follows:
This formula suggests a way to define de Rham cohomology for a 'noncommutative spectrum' of a noncommutative algebra A, which was extensively developed by Connes.
that be defined, unlike K-theory, as the homology of a chain complex
. Cyclic cohomology is in fact endowed with a pairing with K-theory
, and one hopes this pairing to be non-degenerate.
There has been defined a number of variants whose purpose is to fit better with algebras with topology, such as Fréchet algebra
s,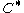
-algebras, etc. The reason is that K-theory
behaves much better on topological algebras such as Banach algebra
s or C*-algebras than on algebras without additional structure. Since, on the other hand, cyclic homology degenerates on C*-algebras, there came up the need to define modified theories. Among them are entire cyclic homology due to Alain Connes
, analytic cyclic homology due to Ralf Meyer or asymptotic and local cyclic homology due to Michael Puschnigg. The last one is very near to K-theory
as it is endowed with a bivariant Chern character from KK-theory
.
s, for deformation quantization (Weyl quantization). The index theorem for quantum tori is linked to the quantum Hall effect, and the index theorem for deformation quantization to the study of band energy redistribution in the Born-Oppenheimer approximation
in molecular physics.
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, cyclic homology and cyclic cohomology are (co)homology theories for associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
s introduced by Alain Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
around 1980, which play an important role in his noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
. They were independently discovered by Boris Tsygan and studied by Connes, Karoubi, Feigin-Tsygan, Loday, Quillen, and others.
Hints about definition
The first definition of the cyclic homology of a ring A over a field of characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero, denoted
- HCn(A) or Hnλ(A),
proceeded by the means of an explicit chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
related to the Hochschild homology complex
Hochschild homology
In mathematics, Hochschild homology is a homology theory for associative algebras over rings. There is also a theory for Hochschild homology of certain functors...
of A. Connes later found a more categorical approach to cyclic homology using a notion of cyclic object in an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, which is analogous to the notion of simplicial object. In this way, cyclic homology (and cohomology) may be interpreted as a derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
, which can be explicitly computed by the means of the Connes bicomplex.
One of the striking features of cyclic homology is the existence of a long exact sequence connecting
Hochschild and cyclic homology. This long exact sequence is referred to as the periodicity sequence.
Case of commutative rings
Cyclic cohomology of the commutative algebra A of regular functions on an affine algebraic variety over a field k of characteristic zero can be computed in terms of Grothendieck's algebraic de Rham complexCrystalline cohomology
In mathematics, crystalline cohomology is a Weil cohomology theory for schemes introduced by and developed by . Its values are modules over rings of Witt vectors over the base field....
. In particular, if the variety V=Spec A is smooth, cyclic cohomology of A are expressed in terms of the de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
of V as follows:
This formula suggests a way to define de Rham cohomology for a 'noncommutative spectrum' of a noncommutative algebra A, which was extensively developed by Connes.
Variants of cyclic homology
One motivation of cyclic homology was the need for an approximation of K-theoryK-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
that be defined, unlike K-theory, as the homology of a chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
. Cyclic cohomology is in fact endowed with a pairing with K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
, and one hopes this pairing to be non-degenerate.
There has been defined a number of variants whose purpose is to fit better with algebras with topology, such as Fréchet algebra
Fréchet algebra
In mathematics, a Fréchet algebra is a topological algebra, in which the topology is given by a countable family of submultiplicative seminorms:and the algebra is complete....
s,
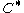-algebras, etc. The reason is that K-theoryK-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
behaves much better on topological algebras such as Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
s or C*-algebras than on algebras without additional structure. Since, on the other hand, cyclic homology degenerates on C*-algebras, there came up the need to define modified theories. Among them are entire cyclic homology due to Alain Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
, analytic cyclic homology due to Ralf Meyer or asymptotic and local cyclic homology due to Michael Puschnigg. The last one is very near to K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
as it is endowed with a bivariant Chern character from KK-theory
KK-theory
In mathematics, KK-theory is a common generalization both of K-homology and K-theory , as an additive bivariant functor on separable C*-algebras...
.
Applications
One of the applications of cyclic homology is to find new proofs and generalizations of the Atiyah-Singer index theorem. Among these generalizations are index theorems for quantum tori and quantum groups, for D-moduleD-module
In mathematics, a D-module is a module over a ring D of differential operators. The major interest of such D-modules is as an approach to the theory of linear partial differential equations...
s, for deformation quantization (Weyl quantization). The index theorem for quantum tori is linked to the quantum Hall effect, and the index theorem for deformation quantization to the study of band energy redistribution in the Born-Oppenheimer approximation
Born-Oppenheimer approximation
In quantum chemistry, the computation of the energy and wavefunction of an average-size molecule is a formidable task that is alleviated by the Born–Oppenheimer approximation, named after Max Born and J. Robert Oppenheimer. For instance the benzene molecule consists of 12 nuclei and 42...
in molecular physics.
See also
- Hochschild homologyHochschild homologyIn mathematics, Hochschild homology is a homology theory for associative algebras over rings. There is also a theory for Hochschild homology of certain functors...
- Noncommutative geometryNoncommutative geometryNoncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
- HomologyHomology (mathematics)In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
- Homology theoryHomology theoryIn mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...