Criss-cross algorithm - AbsoluteAstronomy.com

Optimization (mathematics)

In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....

, the criss-cross algorithm denotes a family of algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

s for linear programming

Linear programming

Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...

. Variants of the criss-cross algorithm also solve more general problems with linear inequality constraints

Linear programming

Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...

and nonlinear

Nonlinear programming

In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...

objective functions

Optimization (mathematics)

In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....

; there are criss-cross algorithms for linear-fractional programming

Linear-fractional programming

In mathematical optimization, linear-fractional programming is a generalization of linear programming . Whereas the objective function in linear programs are linear functions, the objective function in a linear-fractional program is a ratio of two linear functions...

problems, quadratic-programming

Quadratic programming

Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....

problems, and linear complementarity problem

Linear complementarity problem

In mathematical optimization theory, the linear complementarity problem arises frequently in computational mechanics and encompasses the well-known quadratic programming as a special case...

s.

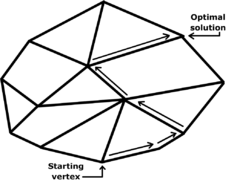
Like the simplex algorithm

Simplex algorithm

In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....

of George B. Dantzig

George Dantzig

George Bernard Dantzig was an American mathematical scientist who made important contributions to operations research, computer science, economics, and statistics....

, the criss-cross algorithm is not a polynomial-time algorithm

Time complexity

In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...

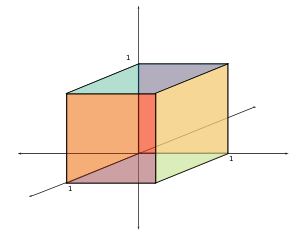
for linear programming. Both algorithms visit all 2^D corners of a (perturbed) cube

Unit cube

A unit cube, sometimes called a cube of side 1, is a cube whose sides are 1 unit long. The volume of a 3-dimensional unit cube is 1 cubic unit, and its total surface area is 6 square units.- Unit Hypercube :...

in dimension D, the Klee–Minty cube

Klee–Minty cube

The Klee–Minty cube is a unit cube whose corners have been slightly perturbed. Klee and Minty demonstrated that Dantzig's simplex algorithm has poor worst-case performance when initialized at one corner of their "squashed cube".In particular, many optimization algorithms for linear optimization...

(after Victor Klee

Victor Klee

Victor L. Klee, Jr. was a mathematician specialising in convex sets, functional analysis, analysis of algorithms, optimization, and combinatorics. He spent almost his entire career at the University of Washington in Seattle.Born in San Francisco, Vic Klee earned his B.A...

and George J. Minty), in the worst case. However, when it is started at a random corner, the criss-cross algorithm on average

Average-case complexity

Average-case complexity is a subfield of computational complexity theory that studies the complexity of algorithms on random inputs.The study of average-case complexity has applications in the theory of cryptography....

visits only D additional corners. Thus, for the three-dimensional cube, the algorithm visits all 8 corners in the worst case and exactly 3 additional corners on average.

History

The criss-cross algorithm was published independently by Tamás Terlaky and by Zhe-Min Wang; related algorithms appeared in unpublished reports by other authors.

Comparison with the simplex algorithm for linear optimization

In linear programming, the criss-cross algorithm pivots between a sequence of bases but differs from the simplex algorithm

Simplex algorithm

of George Dantzig

George Dantzig

George Bernard Dantzig was an American mathematical scientist who made important contributions to operations research, computer science, economics, and statistics....

. The simplex algorithm first finds a (primal-) feasible basis by solving a "phase-one problem"; in "phase two", the simplex algorithm pivots between a sequence of basic feasible solutions so that the objective function is non-decreasing with each pivot, terminating when with an optimal solution (also finally finding a "dual feasible" solution).

The criss-cross algorithm is simpler than the simplex algorithm, because the criss-cross algorithm only has one-phase. Its pivoting rules are similar to the least-index pivoting rule of Bland

Bland's rule

In mathematical optimization, Bland's rule is an algorithmic refinement of the simplex method for linear optimization....

. Bland's rule uses only sign

Sign function

In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....

s of coefficients rather than their (real-number) order when deciding eligible pivots. Bland's rule selects an entering variables by comparing values of reduced costs, using the real-number ordering of the eligible pivots. Unlike Bland's rule, the criss-cross algorithm is "purely combinatorial", selecting an entering variable and a leaving variable by considering only the signs of coefficients rather than their real-number ordering. The criss-cross algorithm has been applied to furnish constructive proofs of basic results in real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

linear algebra

Linear algebra

Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...

, such as the lemma of Farkas.

Description

The criss-cross algorithm has been specified in many publications and implemented in many programming languages.

Computational complexity: Worst and average cases

The time complexity

Time complexity

of an algorithm

Algorithm

counts the number of arithmetic operations sufficient for the algorithm to solve the problem. For example, Gaussian elimination

Gaussian elimination

In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...

requires on the order of D³ operations, and so it is said to have polynomial time-complexity, because its complexity is bounded by a cubic polynomial. There are examples of algorithms that do not have polynomial-time complexity. For example, a generalization of Gaussian elimination called Buchberger's algorithm

Buchberger's algorithm

In computational algebraic geometry and computational commutative algebra, Buchberger's algorithm is a method of transforming a given set of generators for a polynomial ideal into a Gröbner basis with respect to some monomial order. It was invented by Austrian mathematician Bruno Buchberger...

has for its complexity an exponential function of the problem data (the degree of the polynomial

Degree of a polynomial

The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...

s and the number of variables of the multivariate polynomials). Because exponential functions eventually grow much faster than polynomial functions, an exponential complexity implies that an algorithm has slow performance on large problems.

Several algorithms for linear programming—Khachiyan's ellipsoidal algorithm, Karmarkar's projective algorithm

Karmarkar's algorithm

Karmarkar's algorithm is an algorithm introduced by Narendra Karmarkar in 1984 for solving linear programming problems. It was the first reasonably efficient algorithm that solves these problems in polynomial time...

, and central-path algorithms—have polynomial time-complexity (in the worst case

Worst case complexity

In computer science, the worst-case complexity measures the resources an algorithm requires in the worst-case...

and thus on average). The ellipsoidal and projective algorithms were published before the criss-cross algorithm.

However, like the simplex algorithm of Dantzig, the criss-cross algorithm is not a polynomial-time algorithm for linear programming. Terlaky's criss-cross algorithm visits all the 2^D corners of a (perturbed) cube in dimension D, according to a paper of Roos; Roos's paper modifies the Klee

Victor Klee

–Minty construction of a cube

Unit cube

on which the simplex algorithm takes 2^D steps). Like the simplex algorithm, the criss-cross algorithm visits all 8 corners of the three-dimensional cube in the worst case.

When it is initialized at a random corner of the cube, the criss-cross algorithm visits only D additional corners, however, according to a 1994 paper by Fukuda and Namiki. Trivially, the simplex algorithm takes on average D steps for a cube. Like the simplex algorithm, the criss-cross algorithm visits exactly 3 additional corners of the three-dimensional cube on average.

Variants

The criss-cross algorithm has been extended to solve more general problems than linear programming problems.

Vertex enumeration

The criss-cross algorithm was used in an algorithm for enumerating all the vertices of a polytope

Vertex enumeration problem

In mathematics, the vertex enumeration problem for a polytope, a polyhedral cell complex, a hyperplane arrangement, or some other object of discrete geometry, is the problem of determination of the object's vertices given some formal representation of the object...

, which was published by David Avis

David Avis

David Michael Avis is a Canadian and British computer scientist known for his contributions to geometric computations. Avis is a professor in computational geometry and applied mathematics in the School of Computer Science, McGill University, in Montreal.Avis received his Ph.D. in 1977 from...

and Komei Fukuda in 1992. Avis and Fukuda presented an algorithm which finds the v vertices of a polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

defined by a nondegenerate system of n linear inequalities

Linear inequality

In mathematics a linear inequality is an inequality which involves a linear function.-Definitions:When two expressions are connected by 'greater than' or 'less than' sign, we get an inequation....

in D dimension

Dimension (vector space)

In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...

s (or, dually, the v facet

Facet

Facets are flat faces on geometric shapes. The organization of naturally occurring facets was key to early developments in crystallography, since they reflect the underlying symmetry of the crystal structure...

s of the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

of n points in D dimensions, where each facet contains exactly D given points) in time O(nDv) and O(nD) space.

Oriented matroids

The criss-cross algorithm is often studied using the theory of oriented matroid

Oriented matroid

An oriented matroid is a mathematical structure that abstracts the properties of directed graphs and of arrangements of vectors in a vector space over an ordered field...

s (OMs), which is a combinatorial

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

abstraction of linear-optimization theory. Indeed, Bland's pivoting rule was based on his previous papers on oriented-matroid theory. However, Bland's rule exhibits cycling on some oriented-matroid linear-programming problems. The first purely combinatorial algorithm for linear programming was devised by Michael J. Todd. Todd's algorithm was developed not only for linear-programming in the setting of oriented matroids, but also for quadratic-programming problems

Quadratic programming

and linear-complementarity problem

Linear complementarity problem

In mathematical optimization theory, the linear complementarity problem arises frequently in computational mechanics and encompasses the well-known quadratic programming as a special case...

s. Todd's algorithm is complicated even to state, unfortunately, and its finite-convergence proofs are somewhat complicated.

The criss-cross algorithm and its proof of finite termination can be simply stated and readily extend the setting of oriented matroids. The algorithm can be further simplified for linear feasibility problems, that is for linear system

Linear system

A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....

s with nonnegative variable

Linear inequality

In mathematics a linear inequality is an inequality which involves a linear function.-Definitions:When two expressions are connected by 'greater than' or 'less than' sign, we get an inequation....

s; these problems can be formulated for oriented matroids. The criss-cross algorithm has been adapted for problems that are more complicated than linear programming: There are oriented-matroid variants also for the quadratic-programming problem and for the linear-complementarity problem.

Summary

The criss-cross algorithm is a simply stated algorithm for linear programming. It was the second fully combinatorial algorithm for linear programming. The partially combinatorial simplex algorithm of Bland cycles on some (nonrealizable) oriented matroids. The first fully combinatorial algorithm was published by Todd, and it is also like the simplex algorithm in that it preserves feasibility after the first feasible basis is generated; however, Todd's rule is complicated. The criss-cross algorithm is not a simplex-like algorithm, because it need not maintain feasibility. The criss-cross algorithm does not have polynomial time-complexity, however.

Researchers have extended the criss-cross algorithm for many optimization-problems, including linear-fractional programming. The criss-cross algorithm can solve quadratic programming problems and linear complementarity problems, even in the setting of oriented matroids. Even when generalized, the criss-cross algorithm remains simply stated.

External links

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.