
Linear inequality
Encyclopedia
In mathematics a linear inequality is an inequality which involves a linear function
.
When operating in terms of real number
s, linear inequalities are the ones written in the forms
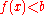 or
or 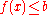 ,
,
where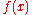 is a linear functional
is a linear functional
in real numbers and b is a constant real number. Alternatively, these may be viewed as
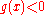 or
or 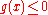 ,
,
where is an affine function.
is an affine function.
The above are commonly written out as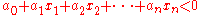
or
Sometimes they may be written out in the forms
or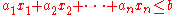
Here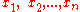 are called the unknowns,
are called the unknowns,  are called the coefficients, and
are called the coefficients, and  is the constant term.
is the constant term.
A linear inequality looks exactly like a linear equation
, with the inequality sign replacing the equality sign.
A system of linear inequalities is a set of linear inequalities in the same variables:
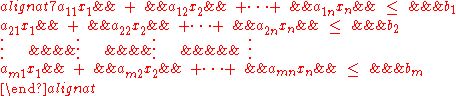
Here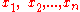 are the unknowns,
are the unknowns,  are the coefficients of the system, and
are the coefficients of the system, and  are the constant terms.
are the constant terms.
This can be concisely written as the matrix
inequality:
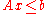
where A is an m×n matrix, x is an n×1 column vector of variables, and b is an m×1 column vector of constants.
In the above systems both strict and non-strict inequalities may be used.
Not all systems of linear inequalities have solutions.
of the n-dimensional real space, one of the two defined by the corresponding linear equation.
The set of solutions of a system of linear inequalities corresponds to the intersection of the half-planes defined by individual inequalities. It is a convex set
, since the half-planes are convex sets, and the intersection of a set of convex sets is also convex. In the non-degenerate cases this convex set is a convex polyhedron (possibly unbounded, e.g., a half-space, a slab between two parallel half-spaces or a polyhedral cone). It may also be empty or a convex polyhedron of lower dimension confined to an affine subspace of the n-dimensional space Rn.
Sets of linear inequalities (called constraints) are used in the definition of linear programming
.
, which will help you find slope
. If slope
is denoted by m and y-intercept
by b, you can find m =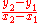 and b =
and b = 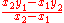 , so long as
, so long as 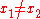 . Such line is described by the equation
. Such line is described by the equation  .
.
The above definition requires well-defined operations of addition
, multiplication
and comparison
, therefore the notion of a linear inequality may be extended to ordered ring
s, in, particular, to ordered field
s.
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
.
Definitions
When two expressions are connected by 'greater than' or 'less than' sign, we get an inequation.When operating in terms of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, linear inequalities are the ones written in the forms
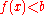 or
or 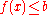 ,
,where
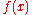 is a linear functional
is a linear functionalLinear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
in real numbers and b is a constant real number. Alternatively, these may be viewed as
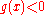 or
or 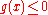 ,
,where
 is an affine function.
is an affine function.The above are commonly written out as
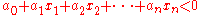
or

Sometimes they may be written out in the forms

or
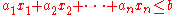
Here
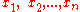 are called the unknowns,
are called the unknowns,  are called the coefficients, and
are called the coefficients, and  is the constant term.
is the constant term.A linear inequality looks exactly like a linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
, with the inequality sign replacing the equality sign.
A system of linear inequalities is a set of linear inequalities in the same variables:
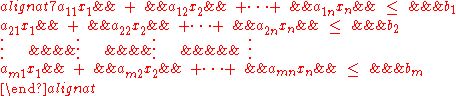
Here
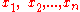 are the unknowns,
are the unknowns,  are the coefficients of the system, and
are the coefficients of the system, and  are the constant terms.
are the constant terms.This can be concisely written as the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
inequality:
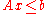
where A is an m×n matrix, x is an n×1 column vector of variables, and b is an m×1 column vector of constants.
In the above systems both strict and non-strict inequalities may be used.
Not all systems of linear inequalities have solutions.
Interpretations and applications
The set of solutions of a real linear inequality constitutes a half-spaceHalf-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
of the n-dimensional real space, one of the two defined by the corresponding linear equation.
The set of solutions of a system of linear inequalities corresponds to the intersection of the half-planes defined by individual inequalities. It is a convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, since the half-planes are convex sets, and the intersection of a set of convex sets is also convex. In the non-degenerate cases this convex set is a convex polyhedron (possibly unbounded, e.g., a half-space, a slab between two parallel half-spaces or a polyhedral cone). It may also be empty or a convex polyhedron of lower dimension confined to an affine subspace of the n-dimensional space Rn.
Sets of linear inequalities (called constraints) are used in the definition of linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
.
Linear inequalities in terms of other mathematical objects
When you graph a linear inequality, it will be on one side of a line. Also, when you mark points where the line crosses where the x and y axis cross each other you can make the rise over runSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
, which will help you find slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
. If slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
is denoted by m and y-intercept
Y-intercept
In coordinate geometry, using the common convention that the horizontal axis represents a variable x and the vertical axis represents a variable y, a y-intercept is a point where the graph of a function or relation intersects with the y-axis of the coordinate system...
by b, you can find m =
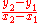 and b =
and b = 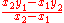 , so long as
, so long as 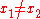 . Such line is described by the equation
. Such line is described by the equation  .
.The above definition requires well-defined operations of addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
and comparison
Comparison
Comparison may refer to:-Language:* Comparison , a feature of many languages* Degree of comparison, an English language grammatical feature* Mass comparison, a test for the relatedness of languages-Mathematics:...
, therefore the notion of a linear inequality may be extended to ordered ring
Ordered ring
In abstract algebra, an ordered ring is a commutative ring R with a total order ≤ such that for all a, b, and c in R:* if a ≤ b then a + c ≤ b + c.* if 0 ≤ a and 0 ≤ b then 0 ≤ ab....
s, in, particular, to ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
s.

