
Convergence of Fourier series
Encyclopedia
In mathematics
, the question of whether the Fourier series
of a periodic function
converges to the given function
is researched by a field known as classical harmonic analysis, a branch of pure mathematics
. Convergence is not necessarily a given in the general case, and there are criteria which need to be met in order for convergence to occur.
Determination of convergence requires the comprehension of pointwise convergence
, uniform convergence, absolute convergence
, Lp spaces
, summability methods and the Cesàro mean.
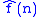 are defined by the formula
are defined by the formula

It is common to describe the connection between ƒ and its Fourier series by
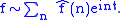
The notation ~ here means that the sum represents the function in some sense. In order to investigate this more carefully, the partial sums need to be defined:
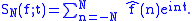
The question we will be interested in is: do the functions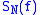 (which are functions of the variable t we omitted in the notation) converge to ƒ and in which sense? Are there conditions on ƒ ensuring this or that type of convergence? This is the main problem discussed in this article.
(which are functions of the variable t we omitted in the notation) converge to ƒ and in which sense? Are there conditions on ƒ ensuring this or that type of convergence? This is the main problem discussed in this article.
Before continuing the Dirichlet's kernel needs to be introduced. Taking the formula for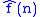 , inserting it into the formula for
, inserting it into the formula for 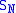 and doing some algebra will give that
and doing some algebra will give that
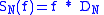
where ∗ stands for the periodic convolution
and is the Dirichlet kernel which has an explicit formula,
is the Dirichlet kernel which has an explicit formula,
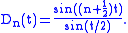
The Dirichlet kernel is not a positive kernel, and in fact, its norm diverges, namely

a fact that will play a crucial role in the discussion. The norm of Dn in L1(T) coincides with the norm of the convolution operator with Dn,
acting on the space C(T) of periodic continuous functions, or with the norm of the linear functional ƒ → (Snƒ)(0) on C(T). Hence, this family of linear functionals on C(T) is unbounded, when n → ∞.
If is an absolutely continuous function,
is an absolutely continuous function,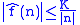
for a constant that only depends on
a constant that only depends on 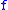 .
.
If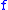 is a bounded variation
is a bounded variation
function,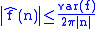
If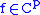
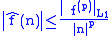
If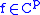 and
and 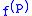 has modulus of continuity
has modulus of continuity
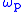 ,
,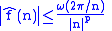
and therefore, if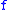 is in the α-Hölder class
is in the α-Hölder class
).
The Dirichlet–Dini Criterion states that: if ƒ is 2π–periodic, locally integrable and satisfies
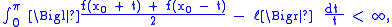
then (Snƒ)(x0) converges to ℓ. This implies that for any function ƒ of any Hölder class
α > 0, the Fourier series converges everywhere to ƒ(x).
It is also known that for any function of bounded variation
, the Fourier series converges everywhere. See also Dini test
.
There exists a continuous function whose Fourier series converges pointwise, but not uniformly; see Antoni Zygmund, Trigonometric Series, vol. 1, Chapter 8, Theorem 1.13, p. 300.
However, the Fourier series of a continuous function
need not converge pointwise. Perhaps the easiest proof uses the non-boundedness of Dirichlet's kernel in L1(T) and the Banach–Steinhaus uniform boundedness principle
. As typical for existence arguments invoking the Baire category theorem
, this proof is nonconstructive. It shows that the family of continuous functions whose Fourier series converges at a given x is of first Baire category
, in the Banach space
of continuous functions on the circle. So in some sense pointwise convergence is atypical, and for most continuous functions the Fourier series does not converge at a given point. However Carleson's theorem
shows that for a given continuous function the Fourier series converges almost everywhere.
 , and
, and 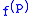 has modulus of continuity
has modulus of continuity
 (we assume here that
(we assume here that  is also non decreasing), then the partial sum of the Fourier series converges to the function with the following speed
is also non decreasing), then the partial sum of the Fourier series converges to the function with the following speed
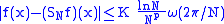
for a constant that does not depend upon
that does not depend upon  , nor
, nor  , nor
, nor  .
.
This theorem, first proved by D Jackson, tells, for example, that if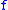 satisfies the
satisfies the  -Hölder condition
-Hölder condition
, then
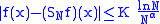
If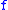 is
is  periodic and absolutely continuous on
periodic and absolutely continuous on  , then the Fourier series of
, then the Fourier series of 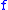 converges uniformly, but not necessarily absolutely, to
converges uniformly, but not necessarily absolutely, to  , see p. 519 Exercise 6 (d) and p. 520 Exercise 7 (c), Introduction to classical real analysis, by Karl R. Stromberg, 1981.
, see p. 519 Exercise 6 (d) and p. 520 Exercise 7 (c), Introduction to classical real analysis, by Karl R. Stromberg, 1981.
Fourier series if

Obviously, if this condition holds then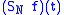 converges absolutely for every t and on the other hand, it is enough that
converges absolutely for every t and on the other hand, it is enough that  converges absolutely for even one t, then this
converges absolutely for even one t, then this
condition will hold. In other words, for absolute convergence there is no issue of where the sum converges absolutely — if it converges absolutely at one point then it does it everywhere.
The family of all functions with absolutely converging Fourier series is a Banach algebra
(the operation of multiplication in the algebra is a simple multiplication of functions). It is called the Wiener algebra
, after Norbert Wiener
, who proved that if ƒ has absolutely converging Fourier
series and is never zero, then 1/ƒ has absolutely converging Fourier series. The original proof of Wiener's theorem was difficult; a simplification using the theory of Banach algebras was given by Israel Gelfand
. Finally, a short elementary proof was given by Donald J. Newman
in 1975.
If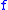 belongs to a α-Hölder class for α > ½ then
belongs to a α-Hölder class for α > ½ then
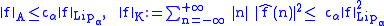
for the constant in the
the constant in the
Hölder condition
,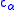 a constant only dependent on
a constant only dependent on  ;
; 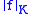 is the norm of the Krein algebra. Notice that the ½ here is essential — there are ½-Hölder functions which do not belong to the Wiener algebra. Besides, this theorem cannot improve the best known bound on the size of the Fourier coefficient of a α-Hölder function - that is only O
is the norm of the Krein algebra. Notice that the ½ here is essential — there are ½-Hölder functions which do not belong to the Wiener algebra. Besides, this theorem cannot improve the best known bound on the size of the Fourier coefficient of a α-Hölder function - that is only O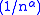 and then not summable!
and then not summable!
If ƒ is of bounded variation
and belongs to a α-Hölder class for some α > 0, it belongs to the Wiener algebra.
, which is a direct transcription of general Hilbert space
results. According to the Riesz–Fischer theorem, if ƒ is square-integrable then
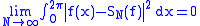
i.e., converges to ƒ in the norm of L2. It is easy to see that the converse is also true: if the limit above is zero, ƒ must be in L2. So this is an if and only if
converges to ƒ in the norm of L2. It is easy to see that the converse is also true: if the limit above is zero, ƒ must be in L2. So this is an if and only if
condition.
If 2 in the exponents above is replaced with some p, the question becomes much harder. It turns out that the convergence still holds if 1 < p < ∞. In other words, for ƒ in Lp
,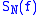 converges to ƒ in the Lp norm. The original proof uses properties of holomorphic function
converges to ƒ in the Lp norm. The original proof uses properties of holomorphic function
s and Hardy space
s, and another proof, due to Salomon Bochner
relies upon the Riesz–Thorin interpolation theorem. For p = 1 and infinity, the result is not true. The construction of an example of divergence in L1 was first done by Andrey Kolmogorov
(see below). For infinity, the result is a more or less trivial corollary of the uniform boundedness principle
.
If the partial summation operator SN is replaced by a suitable summability kernel (for example the Fejér sum obtained by convolution with the Fejér kernel), basic functional analytic techniques can be applied to show that norm convergence holds for 1 ≤ p < ∞.
was posed by Nikolai Lusin in the 1920s and remained open until finally resolved positively in 1966 by Lennart Carleson
. Indeed, Carleson showed that the Fourier expansion of any function in L2 converges almost everywhere. This result is now known as Carleson's theorem
. Later on Richard Hunt generalized this to Lp for any p > 1. Despite a number of attempts at simplifying the proof, it is still one of the most difficult results in analysis.
Contrariwise, Andrey Kolmogorov
, in his very first paper published when he was 21, constructed an example of a function in L1 whose Fourier series diverges almost everywhere (later improved to divergence everywhere).
It might be interesting to note that Jean-Pierre Kahane
and Yitzhak Katznelson proved that for any given set E of measure
zero, there exists a continuous function ƒ such that the Fourier series of ƒ fails to converge on any point
of E.
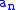 is Cesàro summable to some a if
is Cesàro summable to some a if
It is not difficult to see that if a sequence converges to some a then it is also Cesàro summable to it.
To discuss summability of Fourier series, we must replace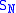 with an appropriate notion. Hence we define
with an appropriate notion. Hence we define
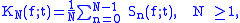
and ask: does converge to f?
converge to f? 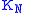 is no longer
is no longer
associated with Dirichlet's kernel, but with Fejér's kernel, namely
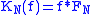
where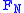 is Fejér's kernel,
is Fejér's kernel,
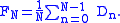
The main difference is that Fejér's kernel is a positive kernel. Fejér's theorem
states that the above sequence of partial sums converge uniformly to ƒ. This implies much better convergence properties
Results about summability can also imply results about regular convergence. For example, we learn that if ƒ is continuous at t, then the Fourier series of ƒ cannot converge to a value different from ƒ(t). It may either converge to ƒ(t) or diverge. This is because, if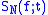 converges to some value x, it is also summable to it, so from the first summability property above, x = ƒ(t).
converges to some value x, it is also summable to it, so from the first summability property above, x = ƒ(t).
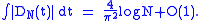
See Big O notation
for the notation O(1). It should be noted that the actual value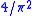 is both difficult to calculate (see Zygmund 8.3) and of almost no use. The fact that for some constant c we have
is both difficult to calculate (see Zygmund 8.3) and of almost no use. The fact that for some constant c we have

is quite clear when one examines the graph of Dirichlet's kernel. The integral over the n-th peak is bigger than c/n and therefore the estimate for the harmonic sum
gives the logarithmic estimate.
This estimate entails quantitative versions of some of the previous results. For any continuous function f and any t one has
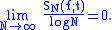
However, for any order of growth ω(n) smaller than log, this no longer holds and it is possible to find a continuous function f such that for some t,
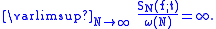
The equivalent problem for divergence everywhere is open. Sergei Konyagin managed to construct an integrable function such that for every t one has
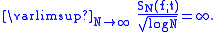
It is not known whether this example is best possible. The only bound from the other direction known is log n.

which are known as "square partial sums". Replacing the sum above with
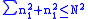
lead to "circular partial sums". The difference between these two definitions is quite notable. For example, the norm of the corresponding Dirichlet kernel for square partial sums is of the order of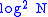 while for circular partial sums it is of the order of
while for circular partial sums it is of the order of  .
.
Many of the results true for one dimension are wrong or unknown in multiple dimensions. In particular, the equivalent of Carleson's theorem is still open for circular partial sums. Almost everywhere convergence of "square partial sums" (as well as more general polygonal partial sums) in multiple dimensions was established around 1970 by Charles Fefferman.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the question of whether the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
of a periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
converges to the given function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is researched by a field known as classical harmonic analysis, a branch of pure mathematics
Pure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
. Convergence is not necessarily a given in the general case, and there are criteria which need to be met in order for convergence to occur.
Determination of convergence requires the comprehension of pointwise convergence
Pointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
, uniform convergence, absolute convergence
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
, Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, summability methods and the Cesàro mean.
Preliminaries
Consider ƒ an integrable function on the interval [0,2π]. For such an ƒ the Fourier coefficients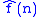 are defined by the formula
are defined by the formula
It is common to describe the connection between ƒ and its Fourier series by
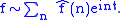
The notation ~ here means that the sum represents the function in some sense. In order to investigate this more carefully, the partial sums need to be defined:
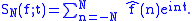
The question we will be interested in is: do the functions
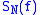 (which are functions of the variable t we omitted in the notation) converge to ƒ and in which sense? Are there conditions on ƒ ensuring this or that type of convergence? This is the main problem discussed in this article.
(which are functions of the variable t we omitted in the notation) converge to ƒ and in which sense? Are there conditions on ƒ ensuring this or that type of convergence? This is the main problem discussed in this article.Before continuing the Dirichlet's kernel needs to be introduced. Taking the formula for
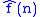 , inserting it into the formula for
, inserting it into the formula for 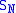 and doing some algebra will give that
and doing some algebra will give that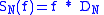
where ∗ stands for the periodic convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
and
 is the Dirichlet kernel which has an explicit formula,
is the Dirichlet kernel which has an explicit formula,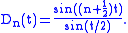
The Dirichlet kernel is not a positive kernel, and in fact, its norm diverges, namely

a fact that will play a crucial role in the discussion. The norm of Dn in L1(T) coincides with the norm of the convolution operator with Dn,
acting on the space C(T) of periodic continuous functions, or with the norm of the linear functional ƒ → (Snƒ)(0) on C(T). Hence, this family of linear functionals on C(T) is unbounded, when n → ∞.
Magnitude of Fourier coefficients
In applications, it is often useful to know the size of the Fourier coefficient.If
 is an absolutely continuous function,
is an absolutely continuous function,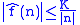
for
 a constant that only depends on
a constant that only depends on 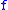 .
.If
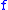 is a bounded variation
is a bounded variationBounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
function,
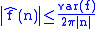
If
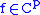
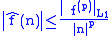
If
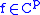 and
and 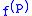 has modulus of continuity
has modulus of continuityModulus of continuity
In mathematical analysis, a modulus of continuity is a function\omega:[0,\infty]\to[0,\infty]used to measure quantitatively the uniform continuity of functions. So, a function f:I\to\R admits \omega as a modulus of continuity if and only if|f-f|\leq\omega,for all x and y in the domain of f...
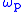 ,
,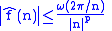
and therefore, if
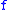 is in the α-Hölder class
is in the α-Hölder class
Pointwise convergence
There are many known sufficient conditions for the Fourier series of a function to converge at a given point x, for example if the function is differentiable at x. Even a jump discontinuity does not pose a problem: if the function has left and right derivatives at x, then the Fourier series will converge to the average of the left and right limits (but see Gibbs phenomenonGibbs phenomenon
In mathematics, the Gibbs phenomenon, named after the American physicist J. Willard Gibbs, is the peculiar manner in which the Fourier series of a piecewise continuously differentiable periodic function behaves at a jump discontinuity: the nth partial sum of the Fourier series has large...
).
The Dirichlet–Dini Criterion states that: if ƒ is 2π–periodic, locally integrable and satisfies
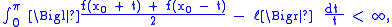
then (Snƒ)(x0) converges to ℓ. This implies that for any function ƒ of any Hölder class
Hölder condition
In mathematics, a real or complex-valued function ƒ on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, \alpha , such that...
α > 0, the Fourier series converges everywhere to ƒ(x).
It is also known that for any function of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
, the Fourier series converges everywhere. See also Dini test
Dini test
In mathematics, the Dini and Dini-Lipschitz tests are highly precise tests that can be used to prove that the Fourier series of a function converges at a given point. These tests are named after Ulisse Dini and Rudolf Lipschitz.- Definition :...
.
There exists a continuous function whose Fourier series converges pointwise, but not uniformly; see Antoni Zygmund, Trigonometric Series, vol. 1, Chapter 8, Theorem 1.13, p. 300.
However, the Fourier series of a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
need not converge pointwise. Perhaps the easiest proof uses the non-boundedness of Dirichlet's kernel in L1(T) and the Banach–Steinhaus uniform boundedness principle
Uniform boundedness principle
In mathematics, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis. Together with the Hahn–Banach theorem and the open mapping theorem, it is considered one of the cornerstones of the field...
. As typical for existence arguments invoking the Baire category theorem
Baire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
, this proof is nonconstructive. It shows that the family of continuous functions whose Fourier series converges at a given x is of first Baire category
Baire space
In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
, in the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
of continuous functions on the circle. So in some sense pointwise convergence is atypical, and for most continuous functions the Fourier series does not converge at a given point. However Carleson's theorem
Carleson's theorem
Carleson's theorem is a fundamental result in mathematical analysis establishing the pointwise almost everywhere convergence of Fourier series of L2 functions, proved by...
shows that for a given continuous function the Fourier series converges almost everywhere.
Uniform convergence
Suppose , and
, and 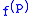 has modulus of continuity
has modulus of continuityModulus of continuity
In mathematical analysis, a modulus of continuity is a function\omega:[0,\infty]\to[0,\infty]used to measure quantitatively the uniform continuity of functions. So, a function f:I\to\R admits \omega as a modulus of continuity if and only if|f-f|\leq\omega,for all x and y in the domain of f...
 (we assume here that
(we assume here that  is also non decreasing), then the partial sum of the Fourier series converges to the function with the following speed
is also non decreasing), then the partial sum of the Fourier series converges to the function with the following speed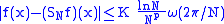
for a constant
 that does not depend upon
that does not depend upon  , nor
, nor  , nor
, nor  .
.This theorem, first proved by D Jackson, tells, for example, that if
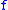 satisfies the
satisfies the  -Hölder condition
-Hölder conditionHölder condition
In mathematics, a real or complex-valued function ƒ on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, \alpha , such that...
, then
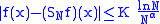
If
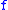 is
is  periodic and absolutely continuous on
periodic and absolutely continuous on  , then the Fourier series of
, then the Fourier series of 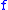 converges uniformly, but not necessarily absolutely, to
converges uniformly, but not necessarily absolutely, to  , see p. 519 Exercise 6 (d) and p. 520 Exercise 7 (c), Introduction to classical real analysis, by Karl R. Stromberg, 1981.
, see p. 519 Exercise 6 (d) and p. 520 Exercise 7 (c), Introduction to classical real analysis, by Karl R. Stromberg, 1981.Absolute convergence
A function ƒ has an absolutely convergingAbsolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
Fourier series if

Obviously, if this condition holds then
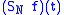 converges absolutely for every t and on the other hand, it is enough that
converges absolutely for every t and on the other hand, it is enough that  converges absolutely for even one t, then this
converges absolutely for even one t, then thiscondition will hold. In other words, for absolute convergence there is no issue of where the sum converges absolutely — if it converges absolutely at one point then it does it everywhere.
The family of all functions with absolutely converging Fourier series is a Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
(the operation of multiplication in the algebra is a simple multiplication of functions). It is called the Wiener algebra
Wiener algebra
In mathematics, the Wiener algebra, named after Norbert Wiener and usually denoted by , is the space of absolutely convergent Fourier series. Here T denotes the circle group.-Banach algebra structure:The norm of a function is given by...
, after Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
, who proved that if ƒ has absolutely converging Fourier
series and is never zero, then 1/ƒ has absolutely converging Fourier series. The original proof of Wiener's theorem was difficult; a simplification using the theory of Banach algebras was given by Israel Gelfand
Israel Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
. Finally, a short elementary proof was given by Donald J. Newman
Donald J. Newman
Donald J. Newman was an American mathematician and professor, excelling at the Putnam mathematics competition while an undergraduate at City College of New York and New York University, and later receiving his PhD from Harvard University in 1953.- Life and works :Newman was born in Brooklyn, New...
in 1975.
If
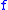 belongs to a α-Hölder class for α > ½ then
belongs to a α-Hölder class for α > ½ then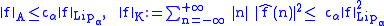
for
 the constant in the
the constant in theHölder condition
Hölder condition
In mathematics, a real or complex-valued function ƒ on d-dimensional Euclidean space satisfies a Hölder condition, or is Hölder continuous, when there are nonnegative real constants C, \alpha , such that...
,
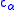 a constant only dependent on
a constant only dependent on  ;
; 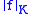 is the norm of the Krein algebra. Notice that the ½ here is essential — there are ½-Hölder functions which do not belong to the Wiener algebra. Besides, this theorem cannot improve the best known bound on the size of the Fourier coefficient of a α-Hölder function - that is only O
is the norm of the Krein algebra. Notice that the ½ here is essential — there are ½-Hölder functions which do not belong to the Wiener algebra. Besides, this theorem cannot improve the best known bound on the size of the Fourier coefficient of a α-Hölder function - that is only O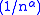 and then not summable!
and then not summable!If ƒ is of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
and belongs to a α-Hölder class for some α > 0, it belongs to the Wiener algebra.
Norm convergence
The simplest case is that of L2Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, which is a direct transcription of general Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
results. According to the Riesz–Fischer theorem, if ƒ is square-integrable then
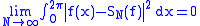
i.e.,
 converges to ƒ in the norm of L2. It is easy to see that the converse is also true: if the limit above is zero, ƒ must be in L2. So this is an if and only if
converges to ƒ in the norm of L2. It is easy to see that the converse is also true: if the limit above is zero, ƒ must be in L2. So this is an if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
condition.
If 2 in the exponents above is replaced with some p, the question becomes much harder. It turns out that the convergence still holds if 1 < p < ∞. In other words, for ƒ in Lp
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
,
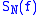 converges to ƒ in the Lp norm. The original proof uses properties of holomorphic function
converges to ƒ in the Lp norm. The original proof uses properties of holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s and Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
s, and another proof, due to Salomon Bochner
Salomon Bochner
Salomon Bochner was an American mathematician of Austrian-Hungarian origin, known for wide-ranging work in mathematical analysis, probability theory and differential geometry.- Life :...
relies upon the Riesz–Thorin interpolation theorem. For p = 1 and infinity, the result is not true. The construction of an example of divergence in L1 was first done by Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
(see below). For infinity, the result is a more or less trivial corollary of the uniform boundedness principle
Uniform boundedness principle
In mathematics, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis. Together with the Hahn–Banach theorem and the open mapping theorem, it is considered one of the cornerstones of the field...
.
If the partial summation operator SN is replaced by a suitable summability kernel (for example the Fejér sum obtained by convolution with the Fejér kernel), basic functional analytic techniques can be applied to show that norm convergence holds for 1 ≤ p < ∞.
Convergence almost everywhere
The problem whether the Fourier series of any continuous function converges almost everywhereAlmost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
was posed by Nikolai Lusin in the 1920s and remained open until finally resolved positively in 1966 by Lennart Carleson
Lennart Carleson
Lennart Axel Edvard Carleson is a Swedish mathematician, known as a leader in the field of harmonic analysis.-Life:He was a student of Arne Beurling and received his Ph.D. from Uppsala University in 1950...
. Indeed, Carleson showed that the Fourier expansion of any function in L2 converges almost everywhere. This result is now known as Carleson's theorem
Carleson's theorem
Carleson's theorem is a fundamental result in mathematical analysis establishing the pointwise almost everywhere convergence of Fourier series of L2 functions, proved by...
. Later on Richard Hunt generalized this to Lp for any p > 1. Despite a number of attempts at simplifying the proof, it is still one of the most difficult results in analysis.
Contrariwise, Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
, in his very first paper published when he was 21, constructed an example of a function in L1 whose Fourier series diverges almost everywhere (later improved to divergence everywhere).
It might be interesting to note that Jean-Pierre Kahane
Jean-Pierre Kahane
Jean-Pierre Kahane is a French mathematician.Kahane attended the École normale supérieure and obtained the agrégation of mathematics in 1949. He then worked for the CNRS from 1949 to 1954, first as an intern and then as a research assistant...
and Yitzhak Katznelson proved that for any given set E of measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
zero, there exists a continuous function ƒ such that the Fourier series of ƒ fails to converge on any point
of E.
Summability
Does the sequence 0,1,0,1,0,1,... (the partial sums of Grandi's series) converge to ½? This does not seem like a very unreasonable generalization of the notion of convergence. Hence we say that any sequence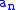 is Cesàro summable to some a if
is Cesàro summable to some a if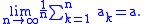
It is not difficult to see that if a sequence converges to some a then it is also Cesàro summable to it.
To discuss summability of Fourier series, we must replace
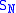 with an appropriate notion. Hence we define
with an appropriate notion. Hence we define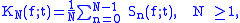
and ask: does
 converge to f?
converge to f? 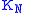 is no longer
is no longerassociated with Dirichlet's kernel, but with Fejér's kernel, namely
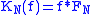
where
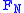 is Fejér's kernel,
is Fejér's kernel,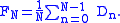
The main difference is that Fejér's kernel is a positive kernel. Fejér's theorem
Fejér's theorem
In mathematics, Fejér's theorem, named for Hungarian mathematician Lipót Fejér, states that if f:R → C is a continuous function with period 2π, then the sequence of Cesàro means of the sequence of partial sums of the Fourier series of f converges uniformly to f on...
states that the above sequence of partial sums converge uniformly to ƒ. This implies much better convergence properties
- If ƒ is continuous at t then the Fourier series of ƒ is summable at t to ƒ(t). If ƒ is continuous, its Fourier series is uniformly summable (i.e.
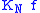 converges uniformly to ƒ).
converges uniformly to ƒ). - For any integrable ƒ,
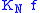 converges to ƒ in the
converges to ƒ in the 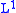 norm.
norm. - There is no Gibbs phenomenon.
Results about summability can also imply results about regular convergence. For example, we learn that if ƒ is continuous at t, then the Fourier series of ƒ cannot converge to a value different from ƒ(t). It may either converge to ƒ(t) or diverge. This is because, if
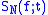 converges to some value x, it is also summable to it, so from the first summability property above, x = ƒ(t).
converges to some value x, it is also summable to it, so from the first summability property above, x = ƒ(t).Order of growth
The order of growth of Dirichlet's kernel is logarithmic, i.e.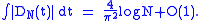
See Big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
for the notation O(1). It should be noted that the actual value
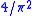 is both difficult to calculate (see Zygmund 8.3) and of almost no use. The fact that for some constant c we have
is both difficult to calculate (see Zygmund 8.3) and of almost no use. The fact that for some constant c we have
is quite clear when one examines the graph of Dirichlet's kernel. The integral over the n-th peak is bigger than c/n and therefore the estimate for the harmonic sum
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
gives the logarithmic estimate.
This estimate entails quantitative versions of some of the previous results. For any continuous function f and any t one has
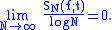
However, for any order of growth ω(n) smaller than log, this no longer holds and it is possible to find a continuous function f such that for some t,
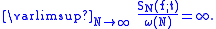
The equivalent problem for divergence everywhere is open. Sergei Konyagin managed to construct an integrable function such that for every t one has
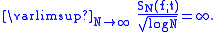
It is not known whether this example is best possible. The only bound from the other direction known is log n.
Multiple dimensions
Upon examining the equivalent problem in more than one dimension, it is necessary to specify the precise order of summation one uses. For example, in two dimensions, one may define
which are known as "square partial sums". Replacing the sum above with
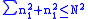
lead to "circular partial sums". The difference between these two definitions is quite notable. For example, the norm of the corresponding Dirichlet kernel for square partial sums is of the order of
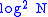 while for circular partial sums it is of the order of
while for circular partial sums it is of the order of  .
.Many of the results true for one dimension are wrong or unknown in multiple dimensions. In particular, the equivalent of Carleson's theorem is still open for circular partial sums. Almost everywhere convergence of "square partial sums" (as well as more general polygonal partial sums) in multiple dimensions was established around 1970 by Charles Fefferman.
Textbooks
- Dunham Jackson "The theory of Approximation", AMS Colloquium Publication Volume XI, New York 1930.
- Nina K. Bary, A treatise on trigonometric series, Vols. I, II. Authorized translation by Margaret F. Mullins. A Pergamon Press Book. The Macmillan Co., New York 1964.
- Antoni Zygmund, Trigonometric series, Vol. I, II. Third edition. With a foreword by Robert A. Fefferman. Cambridge Mathematical Library. Cambridge University Press, Cambridge, 2002. ISBN 0-521-89053-5
- Yitzhak Katznelson, An introduction to harmonic analysis, Third edition. Cambridge University Press, Cambridge, 2004. ISBN 0-521-54359-2
- Karl R. Stromberg, "Introduction to classical analysis", Wadsworth International Group, 1981. ISBN 0-534-98012-0
- The Katznelson book is the one using the most modern terminology and style of the three. The original publishing dates are: Zygmund in 1935, Bari in 1961 and Katznelson in 1968. Zygmund's book was greatly expanded in its second publishing in 1959, however.
Articles referred to in the text
- Paul du Bois Reymond, Ueber die Fourierschen Reihen, Nachr. Kön. Ges. Wiss. Göttingen 21 (1873), 571–582.
- This is the first proof that the Fourier series of a continuous function might diverge. In German
- Andrey Kolmogorov, Une série de Fourier–Lebesgue divergente presque partout, Fundamenta math. 4 (1923), 324–328.
- Andrey Kolmogorov, Une série de Fourier–Lebesgue divergente partout, C. R. Acad. Sci. Paris 183 (1926), 1327–1328
- The first is a construction of an integrable function whose Fourier series diverges almost everywhere. The second is a strengthening to divergence everywhere. In French.
- Lennart Carleson, On convergence and growth of partial sums of Fourier series, Acta Math. 116 (1966) 135–157.
- Richard A. Hunt, On the convergence of Fourier series, Orthogonal Expansions and their Continuous Analogues (Proc. Conf., Edwardsville, Ill., 1967), 235–255. Southern Illinois Univ. Press, Carbondale, Ill.
- Charles Louis Fefferman, Pointwise convergence of Fourier series, Ann. of Math. 98 (1973), 551–571.
- Michael Lacey and Christoph Thiele, A proof of boundedness of the Carleson operator, Math. Res. Lett. 7:4 (2000), 361–370.
- Ole G. Jørsboe and Leif Mejlbro, The Carleson–Hunt theorem on Fourier series. Lecture Notes in Mathematics 911, Springer-Verlag, Berlin-New York, 1982. ISBN 3-540-11198-0
- This is the original paper of Carleson, where he proves that the Fourier expansion of any continuous function converges almost everywhere; the paper of Hunt where he generalizes it to
 spaces; two attempts at simplifying the proof; and a book that gives a self contained exposition of it.
spaces; two attempts at simplifying the proof; and a book that gives a self contained exposition of it.
- D. J. Newman, A simple proof of Wiener's 1/f theorem, Proc. Amer. Math. Soc. 48 (1975), 264–265.
- Jean-Pierre Kahane and Yitzhak Katznelson, Sur les ensembles de divergence des séries trigonométriques, Studia Math. 26 (1966), 305–306
- In this paper the authors show that for any set of zero measure there exists a continuous function on the circle whose Fourier series diverges on that set. In French.
- Sergei Vladimirovich Konyagin, On divergence of trigonometric Fourier series everywhere, C. R. Acad. Sci. Paris 329 (1999), 693–697.
- Jean-Pierre Kahane, Some random series of functions, second edition. Cambridge University Press, 1993. ISBN 0-521-45602-9
- The Konyagin paper proves the
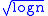 divergence result discussed above. A simpler proof that gives only log log n can be found in Kahane's book.
divergence result discussed above. A simpler proof that gives only log log n can be found in Kahane's book.

