
Wiener algebra
Encyclopedia
In mathematics, the Wiener algebra, named after Norbert Wiener
and usually denoted by , is the space of absolutely convergent
Fourier series
. Here T denotes the circle group.
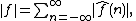
where
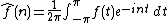
is the nth Fourier coefficient of . The Wiener algebra is closed under pointwise multiplication of functions. Indeed,
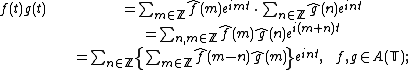
therefore
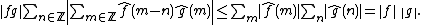
Thus the Wiener algebra is a commutative unitary Banach algebra
. Also, is isomorphic to the Banach algebra , with the isomorphism given by the Fourier transform.
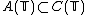
where is the ring of continuous functions on the unit circle.
On the other hand an integration by parts
, together with the Cauchy–Schwarz inequality
and Parseval's formula, shows that
More generally,
for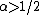 (see ).
(see ).
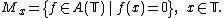
gave a different proof using the spectral theory of commutative C*-algebras. An elementary proof was found by .
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
and usually denoted by , is the space of absolutely convergent
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. Here T denotes the circle group.
Banach algebra structure
The norm of a function is given by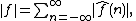
where
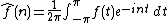
is the nth Fourier coefficient of . The Wiener algebra is closed under pointwise multiplication of functions. Indeed,
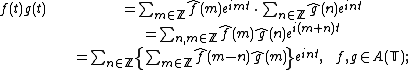
therefore
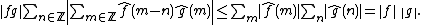
Thus the Wiener algebra is a commutative unitary Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
. Also, is isomorphic to the Banach algebra , with the isomorphism given by the Fourier transform.
Properties
The sum of an absolutely convergent Fourier series is continuous, so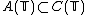
where is the ring of continuous functions on the unit circle.
On the other hand an integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
, together with the Cauchy–Schwarz inequality
Cauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
and Parseval's formula, shows that
-
 .
.
More generally,
for
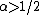 (see ).
(see ).Wiener's 1/f theorem
proved that if has absolutely convergent Fourier series and is never zero, then its inverse also has an absolutely convergent Fourier series. Thus the maximal ideals of are of the form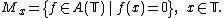
gave a different proof using the spectral theory of commutative C*-algebras. An elementary proof was found by .


