
Computus
Encyclopedia
Computus is the calculation of the date of Easter in the Christian calendar. The name has been used for this procedure since the early Middle Ages
, as it was one of the most important computations of the age.
In principle, the date of Easter is defined as the Sunday following the Full Moon
following vernal equinox (the so-called Paschal Full Moon
).
But neither the vernal equinox nor the full moon are determined by astronomical observation. Instead, a theoretical model known as the Ecclesiastical Full Moon
is used, and the vernal equinox is taken to be set on 21 March. The model assumes that 19 tropical year
s have the same duration as 235 synodal months (modern value: 234.997).
The computus is thus the procedure of determining the first Sunday after the first ecclesiastical full moon that falls on or after 21 March.
Since the Great Schism
of the 11th century, there have been differences in calculation in the Western and Eastern Churches, respectively. Eastern Orthodox Christians
use an ecclesiastical full moon that occurs four to five days later than the western ecclesiastical full moon. The Roman Catholic Church
since 1583 has been using the Gregorian Calendar
to calculate the fixed date of 21 March, while Eastern Churches continue to use the Julian Calendar
.
, at least as early as the meeting (c. 154) of Anicetus
, bishop of Rome, and Polycarp
, bishop of Smyrna
. According to Eusebius' Church History
, quoting Polycrates of Ephesus
, churches in the Roman Province of Asia "always observed the day when the people put away the leaven", the 14th of the lunar month of Nisan. The rest of the Christian world at that time, according to Eusebius, held to "the view which still prevails," of always fixing Easter on Sunday. Eusebius does not say how the Sunday was decided. Other documents from the 3rd and 4th centuries, however, reveal that the customary practice was for Christians to consult their Jewish neighbors to determine when the week of Unleavened Bread would fall, and to set Easter on the Sunday that fell within that week.
By the end of the 3rd century, however, some Christians had become dissatisfied with what they perceived as the disorderly state of the Jewish calendar. The chief complaint was that the Jewish practice sometimes set the 14th of Nisan before the spring equinox. This is implied by Dionysius, bishop of Alexandria in the mid-3rd century, who stated that "at no time other than the spring equinox is it legitimate to celebrate Easter" (Eusebius, Church History 7.20); and by Anatolius of Alexandria (quoted in Eusebius, Church History 7.32) who declared it a "great mistake" to set the Paschal lunar month when the sun is in the twelfth sign of the zodiac. And it was explicitly stated by Peter, bishop of Alexandria that "the men of the present day now celebrate [Passover] before the [spring] equinox...through negligence and error." Another objection to using the Jewish computation may have been that the Jewish calendar was not unified. Jews in one city might have a method for reckoning the Week of Unleavened Bread different from that used by the Jews of another city. Because of these perceived defects in the traditional practice, Christian computists began experimenting with systems for determining Easter that would be free of these defects. But these experiments themselves led to controversy, since some Christians held that the customary practice of holding Easter during the Jewish festival of Unleavened Bread should be continued, even if the Jewish computations were in error from the Christian point of view.
At the First Council of Nicaea
in 325, it was agreed that the Christians should use a common method to establish the date, independent from the Jewish method. However, they made few decisions that were of practical use as guidelines for the computation, and it took several centuries before a common method was accepted throughout Christianity. The process of working out the details generated still further controversies.
The method from Alexandria became authoritative. In its developed form it was based on the epact
s of a reckoned moon according to the 19-year cycle
(a.k.a. the Metonic Cycle). Such a cycle was first proposed by Bishop Anatolius of Laodicea (in present-day Syria), c. 277. Alexandrian Easter tables were composed by Bishop Theophilus
about 390 and within the bishopric of Cyril
about 444. In Constantinople, several computists were active over the centuries after Anatolius (and after the Nicaean Council), but their Easter dates coincided with those of the Alexandrians. Churches on the eastern frontier of the Byzantine Empire
deviated from the Alexandrians during the 6th century, and now celebrate Easter on different dates from Eastern Orthodox churches four times every 532 years. The Alexandrian computus was converted from the Alexandrian calendar
into the Julian calendar in Rome by Dionysius Exiguus
, though only for 95 years. Dionysius introduced the Christian Era
(counting years from the Incarnation of Christ) when he published new Easter tables in 525.
Dionysius's tables replaced earlier methods used by the Church of Rome. The earliest known Roman tables were devised in 222 by Hippolytus of Rome based on 8-year cycles. Then 84-year tables were introduced in Rome by Augustalis
near the end of the 3rd century. These old tables were used in Northumbria until 664, and by isolated monasteries as late as 931. A modified 84-year cycle was adopted in Rome during the first half of the 4th century. Victorius of Aquitaine
tried to adapt the Alexandrian method to Roman rules in 457 in the form of a 532-year table, but he introduced serious errors. These Victorian tables were used in Gaul
(now France) and Spain until they were displaced by Dionysian tables at the end of the 8th century.
In the British Isles Dionysius's and Victorius's tables conflicted with older Roman tables based on an 84-year cycle. The Irish Synod of Mag Léne in 631 decided in favor of either the Dionysian or Victorian Easter and the northern English Synod of Whitby
in 664 adopted the Dionysian tables. The Dionysian reckoning was fully described by Bede
in 725. They may have been adopted by Charlemagne
for the Frankish Church as early as 782 from Alcuin
, a follower of Bede. The Dionysian/Bedan computus remained in use in Western Europe until the Gregorian calendar
reform, and remains in use in most Eastern Churches, including most Eastern Orthodox Church
es and Oriental Orthodox Churches. Churches beyond the eastern frontier of the former Byzantine Empire
use an Easter that differs four times every 532 years from this Easter, including the Assyrian Church of the East
.
The Gregorian Easter has been used since 1583 by the Roman Catholic Church and was adopted by most Protestant churches between 1753 and 1845. German Protestant states used an astronomical Easter based on the Rudolphine Tables
of Johannes Kepler
between 1700 and 1774, while Sweden used it from 1739 to 1844. This astronomical Easter was one week before the Gregorian Easter in 1724, 1744, 1778, 1798, etc.
indicating the beginning of a new lunar month on 1 January, then the lunar year will finish first, and 11 days of the new lunar year will have already passed by the time the new solar year starts. After two years, the difference will have accumulated to 22: the start of lunar months fall 11 days earlier in the solar calendar each year. These days in excess of the solar year over the lunar year are called epacts (Greek: epakta hèmerai). It is necessary to add them to the day of the solar year to obtain the correct day in the lunar year. Whenever the epact reaches or exceeds 30, an extra (so-called embolismic or intercalary) month of 30 days has to be inserted into the lunar calendar; then 30 has to be subtracted from the epact.
Note that leap days are not counted in the schematic lunar calendar: The cycle assigns to the first day of March after the leap-day the same age of the moon that the day would have had if there had been no leap-day. The nineteen-year cycle (Metonic cycle
) assumes that 19 tropical year
s are as long as 235 synodic months. So after 19 years the lunations should fall the same way in the solar years, and the epacts should repeat. However, 19 × 11 = 209 ≡ 29 (mod
30), not 0 (mod 30); that is, 209 divided by 30 leaves a remainder of 29 instead of being an even multiple of 30. So after 19 years, the epact must be corrected by +1 day in order for the cycle to repeat. This is the so-called saltus lunae or moon's leap. The extra 209 days fill seven embolismic months, for a total of 19 × 12 + 7 = 235 lunations. The sequence number of the year in the 19-year cycle is called the "Golden Number
", and is given by the formula
That is, the remainder of the year number Y in the Christian era
when divided by 19, plus one.
Using the method just described, a period of 19 calendar years is also divided into 19 lunar years of 12 or 13 lunar months each. In each calendar year (beginning on 1 January) one of the lunar months must be the first one within the calendar year to have its 14th day (its formal full moon
) on or after 21 March. This lunar month is the Paschal or Easter-month, and Easter is the Sunday after its 14th day (or, saying the same thing, the Sunday within its third week.) The Paschal lunar month always begins on a date in the 29-day period from 8 March to 5 April inclusive. Its 14th day, therefore, always falls on a date between 21 March to 18 April inclusive, and the following Sunday then necessarily falls on a date in the range 22 March to 25 April inclusive. In the solar calendar Easter is called a moveable feast since its date varies within a 35-day range. But in the lunar calendar, Easter is always the third Sunday in the Paschal lunar month, and is no more "moveable" than any holiday that is fixed to a particular day of the week and week within a month.
reform in 1582.
The general method of working was given by Clavius in the Six Canons (1582), and a full explanation followed in his "Explicatio" (1603).
Easter Sunday is the Sunday following the Paschal Full Moon date. The Paschal Full Moon date is the Ecclesiastical Full Moon date following 20 March. The Gregorian method derives Paschal Full Moon dates by determining the epact
for each year. The epact can have a value from * (=0 or 30) to 29 days. The first day of a lunar month is considered the day of the crescent new moon
. The 14th day is considered the day of the full moon
.
Historically the Paschal Full Moon date for a year was found from its sequence number in the Metonic cycle, called the Golden Number
, which cycle repeats the lunar phase on a certain date every 19 years. This method was abandoned in the Gregorian reform because the tabular dates go out of sync with reality after about two centuries, but from the epact method a simplified table can be constructed that has a validity of one to three centuries.
The epacts for the current (2009) Metonic cycle are:
(M=March, A=April)
This table can be extended for previous and following 19-year periods, and is valid from 1900 to 2199.
The epacts are used to find the dates of the New Moon in the following way: Write down a table of all 365 days of the year (the leap day is ignored). Then label all dates with a Roman number counting downwards, from "*" (= 0 or 30), "xxix" (29), down to "i" (1), starting from 1 January, and repeat this to the end of the year. However, in every second such period count only 29 days and label the date with xxv (25) also with xxiv (24). Treat the 13th period (last eleven days) as long, though, and assign the labels "xxv" and "xxiv" to sequential dates (26 and 27 December respectively). Finally, in addition, add the label "25" to the dates that have "xxv" in the 30-day periods; but in 29-day periods (which have "xxiv" together with "xxv") add the label "25" to the date with "xxvi". The distribution of the lengths of the months and the length of the epact cycles is such that each civil calendar month starts and ends with the same epact label, except for February and for the epact labels xxv and 25 in July and August. This table is called the calendarium. The ecclesiastical new moons for any year are those dates at which the epact for the year is entered. If the epact for the year is for instance 27, then there is an ecclesiastical new moon
on every date in that year that has the epact label xxvii (27).
Also label all the dates in the table with letters "A" to "G", starting from 1 January, and repeat to the end of the year. If, for instance, the first Sunday of the year is on 5 January, which has letter E, then every date with the letter "E" will be a Sunday that year. Then "E" is called the Dominical Letter
for that year (from Latin: dies domini, day of the Lord). The Dominical Letter cycles backward one position every year. However, in leap years after 24 February the Sundays will fall on the previous letter of the cycle, so leap years have two Dominical Letters: the first for before, the second for after the leap day.
In practice, for the purpose of calculating Easter, this need not be done for all 365 days of the year. For the epacts, you will find that March comes out exactly the same as January, so one need not calculate January or February. To also avoid the need to calculate the Dominical Letters for January and February, start with D for 1 March. You need the epacts only from 8 March to 5 April. This gives rise to the following table:
.png)
Example: If the epact is, for instance, 27 (Roman xxvii), then there will be an ecclesiastical new moon on every date that has the label "xxvii". The ecclesiastical full moon falls 13 days later. From the table above, this gives a new moon on 4 March and 3 April, and so a full moon on 17 March and 16 April.
Then Easter Day is the first Sunday after the first ecclesiastical full moon on or after 21 March. This definition uses "on or after 21 March" to avoid ambiguity with historic meaning of the word "after". In modern language, this phrase simply means "after 20 March". The definition of "on or after 21 March" is frequently incorrectly abbreviated to "after 21 March" in published and web-based articles, resulting in incorrect Easter dates.
In the example, this Paschal full moon is on 16 April. If the dominical letter is E, then Easter day is on 20 April.
The label 25 (as distinct from "xxv") is used as follows: Within a Metonic cycle, years that are 11 years apart have epacts that differ by one day. Now short lunar months have the labels xxiv and xxv at the same date, so if the epacts 24 and 25 both occur within one Metonic cycle, then in the short months the new (and full) moons would fall on the same dates for these two years. This is not actually possible for the real Moon: the dates should repeat only after 19 years. To avoid this, in years that have epacts 25 and with a Golden Number larger than 11, the reckoned new moon will fall on the date with the label "25" rather than "xxv". In long lunar months, these are the same; in short ones, this is the date which also has the label "xxvi". This does not move the problem to the pair "25" and "xxvi," because that would happen only in year 22 of the cycle, which lasts only 19 years: there is a saltus lunae in between that makes the new moons fall on separate dates.
The Gregorian calendar has a correction to the solar year by dropping three leap days in 400 years (always in a century year). This is a correction to the length of the solar year, but should have no effect on the Metonic relation between years and lunations. Therefore the epact is compensated for this (partially—see epact
) by subtracting one in these century years. This is the so-called solar correction or "solar equation" ("equation" being used in its medieval sense of "correction").
However, 19 uncorrected Julian years are a little longer than 235 lunations. The difference accumulates to one day in about 310 years. Therefore, in the Gregorian calendar, the epact gets corrected by adding 1 eight times in 2500 (Gregorian) years, always in a century year: this is the so-called lunar correction (historically called "lunar equation"). The first one was applied in 1800, and it will be applied every 300 years except for an interval of 400 years between 3900 and 4300, which starts a new cycle.
The solar and lunar corrections work in opposite directions, and in some century years (for example, 1800 and 2100) they cancel each other. The result is that the Gregorian lunar calendar uses an epact table that is valid for a period of from 100 to 300 years. The epact table listed above is valid for the period 1900 to 2199.
Every second lunar month has only 29 days, so one day must have two (of the 30) epact labels assigned to it. The reason for moving around the epact label "xxv/25" rather than any other seems to be the following: According to Dionysius (in his introductory letter to Petronius), the Nicene council, on the authority of Eusebius
, established that the first month of the ecclesiastical lunar year (the Paschal month) should start between 8 March and 5 April inclusive, and the 14th day fall between 21 March and 18 April inclusive, thus spanning a period of (only) 29 days. A new moon on 7 March, which has epact label xxiv, has its 14th day (full moon) on 20 March, which is too early (not following 20 March). So years with an epact of xxiv, if the lunar month beginning on 7 March had 30 days, would have their Paschal new moon on 6 April, which is too late: the full moon would fall on 19 April, and Easter could be as late as 26 April. In the Julian calendar the latest date of Easter was 25 April, and the Gregorian reform maintained that limit. So the Paschal full moon must fall no later than 18 April and the new moon on 5 April, which has epact label xxv. The short month must therefore have its double epact labels on 5 April: xxiv and xxv. Then epact xxv has to be treated differently, as explained in the paragraph above.
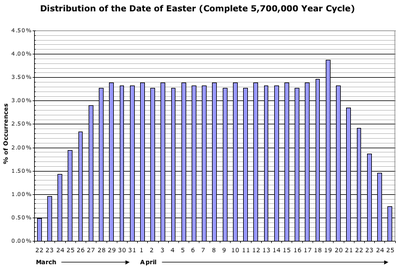
As a consequence, 19 April is the date on which Easter falls most frequently in the Gregorian calendar: in about 3.87% of the years. 22 March is the least frequent, with 0.48%.
 The relation between lunar and solar calendar dates is made independent of the leap day scheme for the solar year. Basically the Gregorian calendar still uses the Julian calendar with a leap day every four years, so a Metonic cycle of 19 years has 6940 or 6939 days with five or four leap days. Now the lunar cycle counts only 19 × 354 + 19 × 11 = 6935 days. By not labeling and counting the leap day with an epact number, but having the next new moon fall on the same calendar date as without the leap day, the current lunation gets extended by a day, and the 235 lunations cover as many days as the 19 years. So the burden of synchronizing the calendar with the moon (intermediate-term accuracy) is shifted to the solar calendar, which may use any suitable intercalation scheme; all under the assumption that 19 solar years = 235 lunations (long-term inaccuracy). A consequence is that the reckoned age of the moon may be off by a day, and also that the lunations which contain the leap day may be 31 days long, which would never happen when the real Moon were followed (short-term inaccuracies). This is the price for a regular fit to the solar calendar.
The relation between lunar and solar calendar dates is made independent of the leap day scheme for the solar year. Basically the Gregorian calendar still uses the Julian calendar with a leap day every four years, so a Metonic cycle of 19 years has 6940 or 6939 days with five or four leap days. Now the lunar cycle counts only 19 × 354 + 19 × 11 = 6935 days. By not labeling and counting the leap day with an epact number, but having the next new moon fall on the same calendar date as without the leap day, the current lunation gets extended by a day, and the 235 lunations cover as many days as the 19 years. So the burden of synchronizing the calendar with the moon (intermediate-term accuracy) is shifted to the solar calendar, which may use any suitable intercalation scheme; all under the assumption that 19 solar years = 235 lunations (long-term inaccuracy). A consequence is that the reckoned age of the moon may be off by a day, and also that the lunations which contain the leap day may be 31 days long, which would never happen when the real Moon were followed (short-term inaccuracies). This is the price for a regular fit to the solar calendar.
From the perspective of those who might wish to use the Gregorian Easter cycle as a calendar for the entire year, there are some flaws in the Gregorian lunar calendar. However, they have no effect on the Paschal month and the date of Easter:
A careful analysis shows that through the way they are used and corrected in the Gregorian calendar, the epacts are actually fractions of a lunation (1/30, also known as a tithi
) and not full days. See epact
for a discussion.
The solar and lunar corrections repeat after 4 × 25 = 100 centuries. In that period, the epact has changed by a total of −1 × (3/4) × 100 + 1 × (8/25) × 100 = −43 ≡ 17 mod 30. This is prime to the 30 possible epacts, so it takes 100 × 30 = 3000 centuries before the epacts repeat; and 3000 × 19 = 57,000 centuries before the epacts repeat at the same Golden Number. This period has (5,700,000/19) × 235 + (−43/30) × (57,000/100) = 70,499,183 lunations. So the Gregorian Easter dates repeat in exactly the same order only after 5,700,000 years = 70,499,183 lunations = 2,081,882,250 days. However, the calendar will already have to have been adjusted after some millennia because of changes in the length of the vernal equinox year, the synodic month, and the day.
This raises the question why the Gregorian lunar calendar has separate solar and lunar corrections, which sometimes cancel each other; instead, the net 4×8 − 3×25 = 43 epact subtractions could be distributed evenly over 10,000 years (as has been proposed for example by Dr. Heiner Lichtenberg). Lilius' original work has not been preserved and Clavius does not explain this. The "solar corrections" approximately undo the effect of the Gregorian modifications to the leap days of the solar calendar, onto the lunar calendar: it (partially) brings the epact cycle back to the original Metonic relation between the Julian year and lunar month. The inherent mismatch between Sun and Moon in this basic 19-year cycle is then corrected every three or four centuries by the "lunar correction" to the epacts. However, the epact corrections occur at the beginning of Gregorian centuries, not Julian centuries, and therefore the original Julian Metonic cycle is not fully restored.
The drift in ecclesiastical full moons calculated by the Gregorian method compared to the true full moons is dominated by the gradual slowing of the Earth's rotation. Borkowski estimated that in the year 12,000 the Gregorian calendar would fall behind the tropical year by at least 8, but less than 12 days. The drift of full moons would be a similar amount.
was then still in use, Easter Sunday was defined, from 1662 to 1752 (in accordance with previous practice), by a simple table of dates in the Anglican Prayer Book
(decreed by the Act of Uniformity 1662
). The table was indexed directly by the Golden Number
and the Sunday Letter
, which (in the Easter section of the Book) were presumed to be already known.
For the British Empire and colonies, the new determination of the Date of Easter Sunday was defined by what is now called the Calendar (New Style) Act 1750
with its Annexe. The method was chosen to give dates agreeing with the Gregorian rule already in use elsewhere. It was required by the Act to be put in the Book of Common Prayer
, and therefore it is the general Anglican rule. The original Act can be seen in the British Statutes at Large 1765. The Annexe to the Act includes the definition: "Easter-day (on which the rest depend) is always the first Sunday after the Full Moon, which happens upon, or next after the Twenty-first Day of March. And if the Full Moon happens upon a Sunday, Easter-day is the Sunday after." The Annexe subsequently uses the terms "Paschal Full Moon" and "Ecclesiastical Full Moon", making it clear that they approximate to the real Full Moon.
The method is quite distinct from that described above in Gregorian calendar. For a general year, one first determines the Golden Number
, then one uses three Tables to determine the Sunday Letter
, a Cypher, and the date of the Paschal Full Moon
, from which the date of Easter Sunday follows. The Epact does not explicitly appear. Simpler tables can be used for limited periods (such as 1900-2199) during which the Cypher (which represents the effect of the Solar and Lunar corrections) does not change. Clavius' details were employed in the construction of the method, but they play no subsequent part in its use.
J R Stockton shows his derivation of an efficient computer algorithm traceable to the Tables in the Prayer Book and the Calendar Act (assuming that a description of how to use the Tables is at hand), and verifies its processes by computing matching Tables.
 The method for computing the date of the ecclesiastical full moon that was standard for the Western Church before the Gregorian calendar reform, and is still used today by most Eastern Christians, made use of an uncorrected repetition of the 19-year Metonic cycle
The method for computing the date of the ecclesiastical full moon that was standard for the Western Church before the Gregorian calendar reform, and is still used today by most Eastern Christians, made use of an uncorrected repetition of the 19-year Metonic cycle
in combination with the Julian calendar
. In terms of the method of the epact
s discussed above, it effectively used a single epact table starting with an epact of 0, which was never corrected. In this case, the epact was counted on 22 March, the earliest acceptable date for Easter. This repeats every 19 years, so there are only 19 possible dates for the Paschal Full Moon from 21 March to 18 April inclusive.
Because there are no corrections as there are for the Gregorian calendar, the ecclesiastical full moon drifts away from the true full moon by more than three days every millennium, and is already a few days later. As a result, the Eastern churches celebrate Easter one week later than the Western churches about 50% of the time. (The Eastern Easter is often four or five weeks later because the Julian 20 March is 13 days later than the Gregorian 20 March for years 1900 to 2099.)
The sequence number of a year in the 19-year cycle is called its Golden Number. This term was first used in the computistic poem Massa Compoti by Alexander de Villa Dei in 1200. A later scribe added the Golden Number to tables originally composed by Abbo of Fleury
in 988.
The claim by the Roman Catholic Church
in the 1582 papal bull
Inter gravissimas
, which promulgated the Gregorian calendar
, that it restored "the celebration of Easter according to the rules fixed by ... the great ecumenical council of Nicæa" was based on a false claim by Dionysius Exiguus
(525) that "we determine the date of Easter Day ... in accordance with the proposal agreed upon by the 318 Fathers of the Church at the Council in Nicaea." The First Council of Nicaea
(325) only stated that Easter was to be celebrated by all Christians on the same Sunday—it did not fix any rules to determine which Sunday. The medieval computus was based on the Alexandrian computus, which was developed by the Church of Alexandria during the first decade of the 4th century using the Alexandrian calendar. The Eastern Roman Empire accepted it shortly after 380 after converting the computus to the Julian calendar
. Rome accepted it sometime between the sixth and 9th centuries. The British Isles accepted it during the 7th century except for a few monasteries. Francia (all of Western Europe except Scandinavia (pagan), the British Isles, the Iberian peninsula
, and southern Italy) accepted it during the last quarter of the 8th century. The last Celtic monastery
to accept it, Iona
, did so in 716, whereas the last English monastery to accept it did so in 931. Before these dates other methods were used which resulted in dates for Easter Sunday that sometimes differed by up to five weeks.
This is the table of Paschal Full Moon dates for all Julian years since 931:
(M=March, A=April)
Easter day is the first Sunday after these dates.
So for a given date of the ecclesiastical full moon, there are seven possible Easter dates. The cycle of Sunday letters, however, does not repeat in seven years: because of the interruptions of the leap day every four years, the full cycle in which weekdays recur in the calendar in the same way, is 4 × 7 = 28 years, the so-called solar cycle. So the Easter dates repeated in the same order after 4 × 7 × 19 = 532 years. This Paschal cycle is also called the Victorian cycle, after Victorius of Aquitaine
, who introduced it in Rome in 457. It is first known to have been used by Annianus of Alexandria
at the beginning of the 5th century. It has also sometimes erroneously been called the Dionysian cycle, after Dionysius Exiguus
, who prepared Easter tables that started in 532; but he apparently did not realize that the Alexandrian computus which he described had a 532-year cycle, although he did realize that his 95-year table was not a true cycle. Venerable Bede
(7th century) seems to have been the first to identify the solar cycle and explain the Paschal cycle from the Metonic cycle and the solar cycle.
In medieval western Europe, the dates of the Paschal Full Moon (14 Nisan) given above could be memorized with the help of a 19-line alliterative poem in Latin:
The first half-line of each line gives the date of the Paschal Full Moon from the table above for each year in the 19-year cycle. The second half-line gives the ferial regular, or weekday displacement, of the day of that year's Paschal Full Moon from the concurrent, or the weekday of 24 March. The ferial regular is repeated in Roman numerals in the third column.
, subtraction
, multiplication
, division
, modulo
, and assignment
(plus minus times div mod assign). That is compatible with the use of simple mechanical or electronic calculators. But it is an undesirable restriction for computer programming, where conditional operators and statements, as well as look-up tables, are always available. One can easily see how conversion from Day-of-March (22 to 56) to Day-and-Month (22 March to 25 April) can be done as
(if DoM>31) {Day=DoM-31, Month=Apr} else {Day=DoM, Month=Mar}.
More importantly, using such conditionals also simplifies the core of the Gregorian calculation.
presented this algorithm for calculating the date of the Julian or Gregorian Easter in 1800 except for one step that he corrected in 1816. In 1800 he incorrectly stated . In 1807 he replaced the condition with the simpler . In 1811 he limited his algorithm to the 18th and 19th centuries only, and stated that 26 April is always replaced with 19 April and 25 April by 18 April. In 1816 he thanked his student Peter Paul Tittel for pointing out that p was wrong in 1800.
in 1876. It has been reprinted many times, in 1877 by Samuel Butcher in The Ecclesiastical Calendar, in 1922 by H. Spencer Jones
in General Astronomy, in 1977 by the Journal of the British Astronomical Association, in 1977 by The Old Farmer's Almanac
, in 1988 by Peter Duffett-Smith in Practical Astronomy with your Calculator
, and in 1991 by Jean Meeus
in Astronomical Algorithms.
, in his book Astronomical Algorithms (1991, p. 69), presents the following algorithm for calculating the Julian Easter in the Julian calendar. This is not the Gregorian Easter now used by Western churches. To obtain the Eastern Orthodox Easter normally given in the Gregorian calendar, 13 days must be added to these Julian Easter dates between 1900 and 2099 inclusive as shown.
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
, as it was one of the most important computations of the age.
In principle, the date of Easter is defined as the Sunday following the Full Moon
Full Moon
Full moon is a lunar phase.Full Moon may also refer to:- Literature :* Full Moon , a novel by P. G. Wodehouse* Full Moon o Sagashite or Full Moon, a manga* Full Moon Press, an American small-press publisher...
following vernal equinox (the so-called Paschal Full Moon
Paschal Full Moon
Notionally, the paschal full moon refers to the ecclesiastical full moon of the northern spring used in the determination of the date of Easter. The name "paschal" is derived from "Pascha", a transliteration of the Greek word, which is itself a transliteration of the Hebrew pesach, both words...
).
But neither the vernal equinox nor the full moon are determined by astronomical observation. Instead, a theoretical model known as the Ecclesiastical Full Moon
Ecclesiastical full moon
An ecclesiastical full moon is the fourteenth day of a lunar month in an ecclesiastical lunar calendar. The ecclesiastical lunar calendar spans the year with lunar months of 30 and 29 days which are intended to approximate the observed phases of the moon...
is used, and the vernal equinox is taken to be set on 21 March. The model assumes that 19 tropical year
Tropical year
A tropical year , for general purposes, is the length of time that the Sun takes to return to the same position in the cycle of seasons, as seen from Earth; for example, the time from vernal equinox to vernal equinox, or from summer solstice to summer solstice...
s have the same duration as 235 synodal months (modern value: 234.997).
The computus is thus the procedure of determining the first Sunday after the first ecclesiastical full moon that falls on or after 21 March.
Since the Great Schism
East–West Schism
The East–West Schism of 1054, sometimes known as the Great Schism, formally divided the State church of the Roman Empire into Eastern and Western branches, which later became known as the Eastern Orthodox Church and the Roman Catholic Church, respectively...
of the 11th century, there have been differences in calculation in the Western and Eastern Churches, respectively. Eastern Orthodox Christians
Eastern Orthodox Church
The Orthodox Church, officially called the Orthodox Catholic Church and commonly referred to as the Eastern Orthodox Church, is the second largest Christian denomination in the world, with an estimated 300 million adherents mainly in the countries of Belarus, Bulgaria, Cyprus, Georgia, Greece,...
use an ecclesiastical full moon that occurs four to five days later than the western ecclesiastical full moon. The Roman Catholic Church
Roman Catholic Church
The Catholic Church, also known as the Roman Catholic Church, is the world's largest Christian church, with over a billion members. Led by the Pope, it defines its mission as spreading the gospel of Jesus Christ, administering the sacraments and exercising charity...
since 1583 has been using the Gregorian Calendar
Gregorian calendar
The Gregorian calendar, also known as the Western calendar, or Christian calendar, is the internationally accepted civil calendar. It was introduced by Pope Gregory XIII, after whom the calendar was named, by a decree signed on 24 February 1582, a papal bull known by its opening words Inter...
to calculate the fixed date of 21 March, while Eastern Churches continue to use the Julian Calendar
Julian calendar
The Julian calendar began in 45 BC as a reform of the Roman calendar by Julius Caesar. It was chosen after consultation with the astronomer Sosigenes of Alexandria and was probably designed to approximate the tropical year .The Julian calendar has a regular year of 365 days divided into 12 months...
.
History
Easter is the most important Christian feast. Accordingly, the proper date of its celebration has been a cause of much controversyEaster controversy
The Easter controversy is a series of controversies about the proper date to celebrate the Christian holiday of Easter. To date, there are four distinct historical phases of the dispute and the dispute has yet to be resolved...
, at least as early as the meeting (c. 154) of Anicetus
Pope Anicetus
Pope Saint Anicetus was Pope of the Catholic Church from about 150 to about 167 . His name is Greek for unconquered...
, bishop of Rome, and Polycarp
Polycarp
Saint Polycarp was a 2nd century Christian bishop of Smyrna. According to the Martyrdom of Polycarp, he died a martyr, bound and burned at the stake, then stabbed when the fire failed to touch him...
, bishop of Smyrna
Smyrna
Smyrna was an ancient city located at a central and strategic point on the Aegean coast of Anatolia. Thanks to its advantageous port conditions, its ease of defence and its good inland connections, Smyrna rose to prominence. The ancient city is located at two sites within modern İzmir, Turkey...
. According to Eusebius' Church History
Church History (Eusebius)
The Church History of Eusebius, the bishop of Caesarea was a 4th-century pioneer work giving a chronological account of the development of Early Christianity from the 1st century to the 4th century. It was written in Koine Greek, and survives also in Latin, Syriac and Armenian manuscripts...
, quoting Polycrates of Ephesus
Polycrates of Ephesus
Polycrates of Ephesus was an Early Christian bishop who resided in Ephesus.Roberts and Donaldson noted that Polycrates "belonged to a family in which he was the eighth Christian bishop; and he presided over the church of Ephesus, in which the traditions of St. John were yet fresh in men's minds at...
, churches in the Roman Province of Asia "always observed the day when the people put away the leaven", the 14th of the lunar month of Nisan. The rest of the Christian world at that time, according to Eusebius, held to "the view which still prevails," of always fixing Easter on Sunday. Eusebius does not say how the Sunday was decided. Other documents from the 3rd and 4th centuries, however, reveal that the customary practice was for Christians to consult their Jewish neighbors to determine when the week of Unleavened Bread would fall, and to set Easter on the Sunday that fell within that week.
By the end of the 3rd century, however, some Christians had become dissatisfied with what they perceived as the disorderly state of the Jewish calendar. The chief complaint was that the Jewish practice sometimes set the 14th of Nisan before the spring equinox. This is implied by Dionysius, bishop of Alexandria in the mid-3rd century, who stated that "at no time other than the spring equinox is it legitimate to celebrate Easter" (Eusebius, Church History 7.20); and by Anatolius of Alexandria (quoted in Eusebius, Church History 7.32) who declared it a "great mistake" to set the Paschal lunar month when the sun is in the twelfth sign of the zodiac. And it was explicitly stated by Peter, bishop of Alexandria that "the men of the present day now celebrate [Passover] before the [spring] equinox...through negligence and error." Another objection to using the Jewish computation may have been that the Jewish calendar was not unified. Jews in one city might have a method for reckoning the Week of Unleavened Bread different from that used by the Jews of another city. Because of these perceived defects in the traditional practice, Christian computists began experimenting with systems for determining Easter that would be free of these defects. But these experiments themselves led to controversy, since some Christians held that the customary practice of holding Easter during the Jewish festival of Unleavened Bread should be continued, even if the Jewish computations were in error from the Christian point of view.
At the First Council of Nicaea
First Council of Nicaea
The First Council of Nicaea was a council of Christian bishops convened in Nicaea in Bithynia by the Roman Emperor Constantine I in AD 325...
in 325, it was agreed that the Christians should use a common method to establish the date, independent from the Jewish method. However, they made few decisions that were of practical use as guidelines for the computation, and it took several centuries before a common method was accepted throughout Christianity. The process of working out the details generated still further controversies.
The method from Alexandria became authoritative. In its developed form it was based on the epact
Epact
The epact was originally defined as the age of the moon in days on January 1, and occurs primarily in connection with tabular methods for determining the date of Easter...
s of a reckoned moon according to the 19-year cycle
Metonic cycle
In astronomy and calendar studies, the Metonic cycle or Enneadecaeteris is a period of very close to 19 years which is remarkable for being very nearly a common multiple of the solar year and the synodic month...
(a.k.a. the Metonic Cycle). Such a cycle was first proposed by Bishop Anatolius of Laodicea (in present-day Syria), c. 277. Alexandrian Easter tables were composed by Bishop Theophilus
Theophilus of Alexandria
Theophilus of Alexandria was Patriarch of Alexandria, Egypt, from 385 to 412. He is regarded as a saint by the Coptic Orthodox Church....
about 390 and within the bishopric of Cyril
Cyril of Alexandria
Cyril of Alexandria was the Patriarch of Alexandria from 412 to 444. He came to power when the city was at its height of influence and power within the Roman Empire. Cyril wrote extensively and was a leading protagonist in the Christological controversies of the later 4th and 5th centuries...
about 444. In Constantinople, several computists were active over the centuries after Anatolius (and after the Nicaean Council), but their Easter dates coincided with those of the Alexandrians. Churches on the eastern frontier of the Byzantine Empire
Byzantine Empire
The Byzantine Empire was the Eastern Roman Empire during the periods of Late Antiquity and the Middle Ages, centred on the capital of Constantinople. Known simply as the Roman Empire or Romania to its inhabitants and neighbours, the Empire was the direct continuation of the Ancient Roman State...
deviated from the Alexandrians during the 6th century, and now celebrate Easter on different dates from Eastern Orthodox churches four times every 532 years. The Alexandrian computus was converted from the Alexandrian calendar
Coptic calendar
The Coptic calendar, also called the Alexandrian calendar, is used by the Coptic Orthodox Church and still used in Egypt. This calendar is based on the ancient Egyptian calendar...
into the Julian calendar in Rome by Dionysius Exiguus
Dionysius Exiguus
Dionysius Exiguus was a 6th-century monk born in Scythia Minor, modern Dobruja shared by Romania and Bulgaria. He was a member of the Scythian monks community concentrated in Tomis, the major city of Scythia Minor...
, though only for 95 years. Dionysius introduced the Christian Era
Anno Domini
and Before Christ are designations used to label or number years used with the Julian and Gregorian calendars....
(counting years from the Incarnation of Christ) when he published new Easter tables in 525.
Dionysius's tables replaced earlier methods used by the Church of Rome. The earliest known Roman tables were devised in 222 by Hippolytus of Rome based on 8-year cycles. Then 84-year tables were introduced in Rome by Augustalis
Augustalis (bishop)
Augustalis was the first bishop of Toulon, according to some authorities. He was appointed in 441. He attended the Council of Orange that year, and the Council of Vaison the following. He is associated with the civitas of Arles by the Martyrologium Hieronymianum, which honors him on September 7...
near the end of the 3rd century. These old tables were used in Northumbria until 664, and by isolated monasteries as late as 931. A modified 84-year cycle was adopted in Rome during the first half of the 4th century. Victorius of Aquitaine
Victorius of Aquitaine
Victorius of Aquitaine, a countryman of Prosper of Aquitaine and also working in Rome, produced in 457 an Easter Cycle, which was based on the consular list provided by Prosper's Chronicle. This dependency caused scholars to think that Prosper had been working on his own Easter Annals for quite...
tried to adapt the Alexandrian method to Roman rules in 457 in the form of a 532-year table, but he introduced serious errors. These Victorian tables were used in Gaul
Gaul
Gaul was a region of Western Europe during the Iron Age and Roman era, encompassing present day France, Luxembourg and Belgium, most of Switzerland, the western part of Northern Italy, as well as the parts of the Netherlands and Germany on the left bank of the Rhine. The Gauls were the speakers of...
(now France) and Spain until they were displaced by Dionysian tables at the end of the 8th century.
In the British Isles Dionysius's and Victorius's tables conflicted with older Roman tables based on an 84-year cycle. The Irish Synod of Mag Léne in 631 decided in favor of either the Dionysian or Victorian Easter and the northern English Synod of Whitby
Synod of Whitby
The Synod of Whitby was a seventh century Northumbriansynod where King Oswiu of Northumbria ruled that his kingdom would calculate Easter and observe the monastic tonsure according to the customs of Rome, rather than the customs practised by Iona and its satellite institutions...
in 664 adopted the Dionysian tables. The Dionysian reckoning was fully described by Bede
Bede
Bede , also referred to as Saint Bede or the Venerable Bede , was a monk at the Northumbrian monastery of Saint Peter at Monkwearmouth, today part of Sunderland, England, and of its companion monastery, Saint Paul's, in modern Jarrow , both in the Kingdom of Northumbria...
in 725. They may have been adopted by Charlemagne
Charlemagne
Charlemagne was King of the Franks from 768 and Emperor of the Romans from 800 to his death in 814. He expanded the Frankish kingdom into an empire that incorporated much of Western and Central Europe. During his reign, he conquered Italy and was crowned by Pope Leo III on 25 December 800...
for the Frankish Church as early as 782 from Alcuin
Alcuin
Alcuin of York or Ealhwine, nicknamed Albinus or Flaccus was an English scholar, ecclesiastic, poet and teacher from York, Northumbria. He was born around 735 and became the student of Archbishop Ecgbert at York...
, a follower of Bede. The Dionysian/Bedan computus remained in use in Western Europe until the Gregorian calendar
Gregorian calendar
The Gregorian calendar, also known as the Western calendar, or Christian calendar, is the internationally accepted civil calendar. It was introduced by Pope Gregory XIII, after whom the calendar was named, by a decree signed on 24 February 1582, a papal bull known by its opening words Inter...
reform, and remains in use in most Eastern Churches, including most Eastern Orthodox Church
Eastern Orthodox Church
The Orthodox Church, officially called the Orthodox Catholic Church and commonly referred to as the Eastern Orthodox Church, is the second largest Christian denomination in the world, with an estimated 300 million adherents mainly in the countries of Belarus, Bulgaria, Cyprus, Georgia, Greece,...
es and Oriental Orthodox Churches. Churches beyond the eastern frontier of the former Byzantine Empire
Byzantine Empire
The Byzantine Empire was the Eastern Roman Empire during the periods of Late Antiquity and the Middle Ages, centred on the capital of Constantinople. Known simply as the Roman Empire or Romania to its inhabitants and neighbours, the Empire was the direct continuation of the Ancient Roman State...
use an Easter that differs four times every 532 years from this Easter, including the Assyrian Church of the East
Assyrian Church of the East
The Assyrian Church of the East, officially the Holy Apostolic Catholic Assyrian Church of the East ʻIttā Qaddishtā w-Shlikhāitā Qattoliqi d-Madnĕkhā d-Āturāyē), is a Syriac Church historically centered in Mesopotamia. It is one of the churches that claim continuity with the historical...
.
The Gregorian Easter has been used since 1583 by the Roman Catholic Church and was adopted by most Protestant churches between 1753 and 1845. German Protestant states used an astronomical Easter based on the Rudolphine Tables
Rudolphine Tables
The Rudolphine Tables consist of a star catalogue and planetary tables published by Johannes Kepler in 1627 using data from Tycho Brahe's observations.-Previous tables:...
of Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
between 1700 and 1774, while Sweden used it from 1739 to 1844. This astronomical Easter was one week before the Gregorian Easter in 1724, 1744, 1778, 1798, etc.
Theory
To each day in a calendar year, the Easter cycle implicitly assigns a lunar age, which is a whole number from 1 to 30. The moon's age starts at 1 and increases to 29 or 30, then starts over again at 1. Each period of 29 (or 30) days of the moon's age makes up a lunar month. With occasional exceptions, 30-day lunar months alternate with 29-day months. So a lunar year of 12 lunar months is reckoned to have 354 days. The solar year is 11 days longer than the lunar year. Supposing a solar and lunar year start on the same day, with a crescent new moonNew moon
In astronomical terminology, the new moon is the lunar phase that occurs when the Moon, in its monthly orbital motion around Earth, lies between Earth and the Sun, and is therefore in conjunction with the Sun as seen from Earth...
indicating the beginning of a new lunar month on 1 January, then the lunar year will finish first, and 11 days of the new lunar year will have already passed by the time the new solar year starts. After two years, the difference will have accumulated to 22: the start of lunar months fall 11 days earlier in the solar calendar each year. These days in excess of the solar year over the lunar year are called epacts (Greek: epakta hèmerai). It is necessary to add them to the day of the solar year to obtain the correct day in the lunar year. Whenever the epact reaches or exceeds 30, an extra (so-called embolismic or intercalary) month of 30 days has to be inserted into the lunar calendar; then 30 has to be subtracted from the epact.
Note that leap days are not counted in the schematic lunar calendar: The cycle assigns to the first day of March after the leap-day the same age of the moon that the day would have had if there had been no leap-day. The nineteen-year cycle (Metonic cycle
Metonic cycle
In astronomy and calendar studies, the Metonic cycle or Enneadecaeteris is a period of very close to 19 years which is remarkable for being very nearly a common multiple of the solar year and the synodic month...
) assumes that 19 tropical year
Tropical year
A tropical year , for general purposes, is the length of time that the Sun takes to return to the same position in the cycle of seasons, as seen from Earth; for example, the time from vernal equinox to vernal equinox, or from summer solstice to summer solstice...
s are as long as 235 synodic months. So after 19 years the lunations should fall the same way in the solar years, and the epacts should repeat. However, 19 × 11 = 209 ≡ 29 (mod
Modulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
30), not 0 (mod 30); that is, 209 divided by 30 leaves a remainder of 29 instead of being an even multiple of 30. So after 19 years, the epact must be corrected by +1 day in order for the cycle to repeat. This is the so-called saltus lunae or moon's leap. The extra 209 days fill seven embolismic months, for a total of 19 × 12 + 7 = 235 lunations. The sequence number of the year in the 19-year cycle is called the "Golden Number
Golden numbers
A golden number is a number assigned to each year in sequence to indicate the year's position in a 19-year Metonic cycle. They are used in the computus and also in the Runic calendar. The golden number of any Julian or Gregorian calendar year can be calculated by dividing the year by 19, taking...
", and is given by the formula
- GN = Y mod 19 + 1
That is, the remainder of the year number Y in the Christian era
Common Era
Common Era ,abbreviated as CE, is an alternative designation for the calendar era originally introduced by Dionysius Exiguus in the 6th century, traditionally identified with Anno Domini .Dates before the year 1 CE are indicated by the usage of BCE, short for Before the Common Era Common Era...
when divided by 19, plus one.
Using the method just described, a period of 19 calendar years is also divided into 19 lunar years of 12 or 13 lunar months each. In each calendar year (beginning on 1 January) one of the lunar months must be the first one within the calendar year to have its 14th day (its formal full moon
Ecclesiastical full moon
An ecclesiastical full moon is the fourteenth day of a lunar month in an ecclesiastical lunar calendar. The ecclesiastical lunar calendar spans the year with lunar months of 30 and 29 days which are intended to approximate the observed phases of the moon...
) on or after 21 March. This lunar month is the Paschal or Easter-month, and Easter is the Sunday after its 14th day (or, saying the same thing, the Sunday within its third week.) The Paschal lunar month always begins on a date in the 29-day period from 8 March to 5 April inclusive. Its 14th day, therefore, always falls on a date between 21 March to 18 April inclusive, and the following Sunday then necessarily falls on a date in the range 22 March to 25 April inclusive. In the solar calendar Easter is called a moveable feast since its date varies within a 35-day range. But in the lunar calendar, Easter is always the third Sunday in the Paschal lunar month, and is no more "moveable" than any holiday that is fixed to a particular day of the week and week within a month.
Gregorian calendar
This method for the computation of the date of Easter was introduced with the Gregorian calendarGregorian calendar
The Gregorian calendar, also known as the Western calendar, or Christian calendar, is the internationally accepted civil calendar. It was introduced by Pope Gregory XIII, after whom the calendar was named, by a decree signed on 24 February 1582, a papal bull known by its opening words Inter...
reform in 1582.
The general method of working was given by Clavius in the Six Canons (1582), and a full explanation followed in his "Explicatio" (1603).
Easter Sunday is the Sunday following the Paschal Full Moon date. The Paschal Full Moon date is the Ecclesiastical Full Moon date following 20 March. The Gregorian method derives Paschal Full Moon dates by determining the epact
Epact
The epact was originally defined as the age of the moon in days on January 1, and occurs primarily in connection with tabular methods for determining the date of Easter...
for each year. The epact can have a value from * (=0 or 30) to 29 days. The first day of a lunar month is considered the day of the crescent new moon
New moon
In astronomical terminology, the new moon is the lunar phase that occurs when the Moon, in its monthly orbital motion around Earth, lies between Earth and the Sun, and is therefore in conjunction with the Sun as seen from Earth...
. The 14th day is considered the day of the full moon
Full moon
Full moon lunar phase that occurs when the Moon is on the opposite side of the Earth from the Sun. More precisely, a full moon occurs when the geocentric apparent longitudes of the Sun and Moon differ by 180 degrees; the Moon is then in opposition with the Sun.Lunar eclipses can only occur at...
.
Historically the Paschal Full Moon date for a year was found from its sequence number in the Metonic cycle, called the Golden Number
Golden number
Golden number may mean:* Golden number , a number assigned to a calendar year denoting its place in a Metonic cycle* Golden ratio, an irrational mathematical constant with special properties in arts and mathematics...
, which cycle repeats the lunar phase on a certain date every 19 years. This method was abandoned in the Gregorian reform because the tabular dates go out of sync with reality after about two centuries, but from the epact method a simplified table can be constructed that has a validity of one to three centuries.
The epacts for the current (2009) Metonic cycle are:
| Year | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Golden Number |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Epact | 29 | 10 | 21 | 2 | 13 | 24 | 5 | 16 | 27 | 8 | 19 | * | 11 | 22 | 3 | 14 | 25 | 6 | 17 |
| Paschal Full Moon date |
14A | 3A | 23M | 11A | 31M | 18A | 8A | 28M | 16A | 5A | 25M | 13A | 2A | 22M | 10A | 30M | 17A | 7A | 27M |
(M=March, A=April)
This table can be extended for previous and following 19-year periods, and is valid from 1900 to 2199.
The epacts are used to find the dates of the New Moon in the following way: Write down a table of all 365 days of the year (the leap day is ignored). Then label all dates with a Roman number counting downwards, from "*" (= 0 or 30), "xxix" (29), down to "i" (1), starting from 1 January, and repeat this to the end of the year. However, in every second such period count only 29 days and label the date with xxv (25) also with xxiv (24). Treat the 13th period (last eleven days) as long, though, and assign the labels "xxv" and "xxiv" to sequential dates (26 and 27 December respectively). Finally, in addition, add the label "25" to the dates that have "xxv" in the 30-day periods; but in 29-day periods (which have "xxiv" together with "xxv") add the label "25" to the date with "xxvi". The distribution of the lengths of the months and the length of the epact cycles is such that each civil calendar month starts and ends with the same epact label, except for February and for the epact labels xxv and 25 in July and August. This table is called the calendarium. The ecclesiastical new moons for any year are those dates at which the epact for the year is entered. If the epact for the year is for instance 27, then there is an ecclesiastical new moon
Ecclesiastical new moon
An ecclesiastical new moon is the first day of a lunar month in an ecclesiastical lunar calendar. Such months have a whole number of days, 29 or 30, whereas true synodic months can vary from about 29.27 to 29.83 days in length. Medieval authors equated the ecclesiastical new moon with a new...
on every date in that year that has the epact label xxvii (27).
Also label all the dates in the table with letters "A" to "G", starting from 1 January, and repeat to the end of the year. If, for instance, the first Sunday of the year is on 5 January, which has letter E, then every date with the letter "E" will be a Sunday that year. Then "E" is called the Dominical Letter
Dominical letter
Dominical letters are letters A, B, C, D, E, F and G assigned to days in a cycle of seven with the letter A always set against 1 January as an aid for finding the day of the week of a given calendar date and in calculating Easter....
for that year (from Latin: dies domini, day of the Lord). The Dominical Letter cycles backward one position every year. However, in leap years after 24 February the Sundays will fall on the previous letter of the cycle, so leap years have two Dominical Letters: the first for before, the second for after the leap day.
In practice, for the purpose of calculating Easter, this need not be done for all 365 days of the year. For the epacts, you will find that March comes out exactly the same as January, so one need not calculate January or February. To also avoid the need to calculate the Dominical Letters for January and February, start with D for 1 March. You need the epacts only from 8 March to 5 April. This gives rise to the following table:
.png)
| Label | March | DL | April | DL |
|---|---|---|---|---|
| * | 1 | D | ||
| xxix | 2 | E | 1 | G |
| xxviii | 3 | F | 2 | A |
| xxvii | 4 | G | 3 | B |
| xxvi | 5 | A | 4 | C |
| 25 | 6 | B | 4 | C |
| xxv | 6 | B | 5 | D |
| xxiv | 7 | C | 5 | D |
| xxiii | 8 | D | 6 | E |
| xxii | 9 | E | 7 | F |
| xxi | 10 | F | 8 | G |
| xx | 11 | G | 9 | A |
| xix | 12 | A | 10 | B |
| xviii | 13 | B | 11 | C |
| xvii | 14 | C | 12 | D |
| xvi | 15 | D | 13 | E |
| xv | 16 | E | 14 | F |
| xiv | 17 | F | 15 | G |
| xiii | 18 | G | 16 | A |
| xii | 19 | A | 17 | B |
| xi | 20 | B | 18 | C |
| x | 21 | C | 19 | D |
| ix | 22 | D | 20 | E |
| viii | 23 | E | 21 | F |
| vii | 24 | F | 22 | G |
| vi | 25 | G | 23 | A |
| v | 26 | A | 24 | B |
| iv | 27 | B | 25 | C |
| iii | 28 | C | ||
| ii | 29 | D | ||
| i | 30 | E | ||
| * | 31 | F |
Example: If the epact is, for instance, 27 (Roman xxvii), then there will be an ecclesiastical new moon on every date that has the label "xxvii". The ecclesiastical full moon falls 13 days later. From the table above, this gives a new moon on 4 March and 3 April, and so a full moon on 17 March and 16 April.
Then Easter Day is the first Sunday after the first ecclesiastical full moon on or after 21 March. This definition uses "on or after 21 March" to avoid ambiguity with historic meaning of the word "after". In modern language, this phrase simply means "after 20 March". The definition of "on or after 21 March" is frequently incorrectly abbreviated to "after 21 March" in published and web-based articles, resulting in incorrect Easter dates.
In the example, this Paschal full moon is on 16 April. If the dominical letter is E, then Easter day is on 20 April.
The label 25 (as distinct from "xxv") is used as follows: Within a Metonic cycle, years that are 11 years apart have epacts that differ by one day. Now short lunar months have the labels xxiv and xxv at the same date, so if the epacts 24 and 25 both occur within one Metonic cycle, then in the short months the new (and full) moons would fall on the same dates for these two years. This is not actually possible for the real Moon: the dates should repeat only after 19 years. To avoid this, in years that have epacts 25 and with a Golden Number larger than 11, the reckoned new moon will fall on the date with the label "25" rather than "xxv". In long lunar months, these are the same; in short ones, this is the date which also has the label "xxvi". This does not move the problem to the pair "25" and "xxvi," because that would happen only in year 22 of the cycle, which lasts only 19 years: there is a saltus lunae in between that makes the new moons fall on separate dates.
The Gregorian calendar has a correction to the solar year by dropping three leap days in 400 years (always in a century year). This is a correction to the length of the solar year, but should have no effect on the Metonic relation between years and lunations. Therefore the epact is compensated for this (partially—see epact
Epact
The epact was originally defined as the age of the moon in days on January 1, and occurs primarily in connection with tabular methods for determining the date of Easter...
) by subtracting one in these century years. This is the so-called solar correction or "solar equation" ("equation" being used in its medieval sense of "correction").
However, 19 uncorrected Julian years are a little longer than 235 lunations. The difference accumulates to one day in about 310 years. Therefore, in the Gregorian calendar, the epact gets corrected by adding 1 eight times in 2500 (Gregorian) years, always in a century year: this is the so-called lunar correction (historically called "lunar equation"). The first one was applied in 1800, and it will be applied every 300 years except for an interval of 400 years between 3900 and 4300, which starts a new cycle.
The solar and lunar corrections work in opposite directions, and in some century years (for example, 1800 and 2100) they cancel each other. The result is that the Gregorian lunar calendar uses an epact table that is valid for a period of from 100 to 300 years. The epact table listed above is valid for the period 1900 to 2199.
Details
This method of computation has several subtleties:Every second lunar month has only 29 days, so one day must have two (of the 30) epact labels assigned to it. The reason for moving around the epact label "xxv/25" rather than any other seems to be the following: According to Dionysius (in his introductory letter to Petronius), the Nicene council, on the authority of Eusebius
Eusebius of Caesarea
Eusebius of Caesarea also called Eusebius Pamphili, was a Roman historian, exegete and Christian polemicist. He became the Bishop of Caesarea in Palestine about the year 314. Together with Pamphilus, he was a scholar of the Biblical canon...
, established that the first month of the ecclesiastical lunar year (the Paschal month) should start between 8 March and 5 April inclusive, and the 14th day fall between 21 March and 18 April inclusive, thus spanning a period of (only) 29 days. A new moon on 7 March, which has epact label xxiv, has its 14th day (full moon) on 20 March, which is too early (not following 20 March). So years with an epact of xxiv, if the lunar month beginning on 7 March had 30 days, would have their Paschal new moon on 6 April, which is too late: the full moon would fall on 19 April, and Easter could be as late as 26 April. In the Julian calendar the latest date of Easter was 25 April, and the Gregorian reform maintained that limit. So the Paschal full moon must fall no later than 18 April and the new moon on 5 April, which has epact label xxv. The short month must therefore have its double epact labels on 5 April: xxiv and xxv. Then epact xxv has to be treated differently, as explained in the paragraph above.
As a consequence, 19 April is the date on which Easter falls most frequently in the Gregorian calendar: in about 3.87% of the years. 22 March is the least frequent, with 0.48%.

From the perspective of those who might wish to use the Gregorian Easter cycle as a calendar for the entire year, there are some flaws in the Gregorian lunar calendar. However, they have no effect on the Paschal month and the date of Easter:
- Lunations of 31 (and sometimes 28) days occur.
- If a year with Golden Number 19 happens to have epact 19, then the last ecclesiastical new moon falls on 2 December; the next would be due on 1 January. However, at the start of the new year there is a saltus lunae which increases the epact by another unit, and the new moon should have occurred on the previous day. So a new moon is missed. The calendarium of the Missale RomanumRoman MissalThe Roman Missal is the liturgical book that contains the texts and rubrics for the celebration of the Mass in the Roman Rite of the Catholic Church.-Situation before the Council of Trent:...
takes account of this by assigning epact label "19" instead of "20" to 31 December of such a year. It happened every 19 years when the original Gregorian epact table was in effect (for the last time in 1690), and will not happen again until 8511. - If the epact of a year is "20", then there will be an ecclesiastical new moon on 31 December. If that year falls before a century year, then in most cases there will be a solar correction which reduces the epact for the new year by one: the resulting epact * means that another ecclesiastical new moon is counted on 1 January; so formally a lunation of one day has passed. This will happen around the beginning of 4200.
- Other borderline cases occur (much) later, and if the rules are followed strictly and these cases are not specially treated, they will generate successive new moon dates that are 1, 28, 59, or (very rarely) 58 days apart.
A careful analysis shows that through the way they are used and corrected in the Gregorian calendar, the epacts are actually fractions of a lunation (1/30, also known as a tithi
Tithi
In vedic timekeeping, a tithi is a lunar day, or the time it takes for the longitudinal angle between the moon and the sun to increase by 12°. Tithis begin at varying times of day and vary in duration from approximately 19 to approximately 26 hours. There are 30 tithis in each lunar month, named...
) and not full days. See epact
Epact
The epact was originally defined as the age of the moon in days on January 1, and occurs primarily in connection with tabular methods for determining the date of Easter...
for a discussion.
The solar and lunar corrections repeat after 4 × 25 = 100 centuries. In that period, the epact has changed by a total of −1 × (3/4) × 100 + 1 × (8/25) × 100 = −43 ≡ 17 mod 30. This is prime to the 30 possible epacts, so it takes 100 × 30 = 3000 centuries before the epacts repeat; and 3000 × 19 = 57,000 centuries before the epacts repeat at the same Golden Number. This period has (5,700,000/19) × 235 + (−43/30) × (57,000/100) = 70,499,183 lunations. So the Gregorian Easter dates repeat in exactly the same order only after 5,700,000 years = 70,499,183 lunations = 2,081,882,250 days. However, the calendar will already have to have been adjusted after some millennia because of changes in the length of the vernal equinox year, the synodic month, and the day.
This raises the question why the Gregorian lunar calendar has separate solar and lunar corrections, which sometimes cancel each other; instead, the net 4×8 − 3×25 = 43 epact subtractions could be distributed evenly over 10,000 years (as has been proposed for example by Dr. Heiner Lichtenberg). Lilius' original work has not been preserved and Clavius does not explain this. The "solar corrections" approximately undo the effect of the Gregorian modifications to the leap days of the solar calendar, onto the lunar calendar: it (partially) brings the epact cycle back to the original Metonic relation between the Julian year and lunar month. The inherent mismatch between Sun and Moon in this basic 19-year cycle is then corrected every three or four centuries by the "lunar correction" to the epacts. However, the epact corrections occur at the beginning of Gregorian centuries, not Julian centuries, and therefore the original Julian Metonic cycle is not fully restored.
The drift in ecclesiastical full moons calculated by the Gregorian method compared to the true full moons is dominated by the gradual slowing of the Earth's rotation. Borkowski estimated that in the year 12,000 the Gregorian calendar would fall behind the tropical year by at least 8, but less than 12 days. The drift of full moons would be a similar amount.
British Calendar Act and Book of Common Prayer
The portion of the Tabular methods section above describes the historical arguments and methods by which the present dates of Easter Sunday were decided in the late 16th century by the Roman Catholic Church. In Britain, where the Julian CalendarJulian calendar
The Julian calendar began in 45 BC as a reform of the Roman calendar by Julius Caesar. It was chosen after consultation with the astronomer Sosigenes of Alexandria and was probably designed to approximate the tropical year .The Julian calendar has a regular year of 365 days divided into 12 months...
was then still in use, Easter Sunday was defined, from 1662 to 1752 (in accordance with previous practice), by a simple table of dates in the Anglican Prayer Book
Book of Common Prayer
The Book of Common Prayer is the short title of a number of related prayer books used in the Anglican Communion, as well as by the Continuing Anglican, "Anglican realignment" and other Anglican churches. The original book, published in 1549 , in the reign of Edward VI, was a product of the English...
(decreed by the Act of Uniformity 1662
Act of Uniformity 1662
The Act of Uniformity was an Act of the Parliament of England, 13&14 Ch.2 c. 4 ,The '16 Charles II c. 2' nomenclature is reference to the statute book of the numbered year of the reign of the named King in the stated chapter...
). The table was indexed directly by the Golden Number
Golden numbers
A golden number is a number assigned to each year in sequence to indicate the year's position in a 19-year Metonic cycle. They are used in the computus and also in the Runic calendar. The golden number of any Julian or Gregorian calendar year can be calculated by dividing the year by 19, taking...
and the Sunday Letter
Dominical letter
Dominical letters are letters A, B, C, D, E, F and G assigned to days in a cycle of seven with the letter A always set against 1 January as an aid for finding the day of the week of a given calendar date and in calculating Easter....
, which (in the Easter section of the Book) were presumed to be already known.
For the British Empire and colonies, the new determination of the Date of Easter Sunday was defined by what is now called the Calendar (New Style) Act 1750
Calendar (New Style) Act 1750
The Calendar Act 1750 is an Act of the Parliament of Great Britain...
with its Annexe. The method was chosen to give dates agreeing with the Gregorian rule already in use elsewhere. It was required by the Act to be put in the Book of Common Prayer
Book of Common Prayer
The Book of Common Prayer is the short title of a number of related prayer books used in the Anglican Communion, as well as by the Continuing Anglican, "Anglican realignment" and other Anglican churches. The original book, published in 1549 , in the reign of Edward VI, was a product of the English...
, and therefore it is the general Anglican rule. The original Act can be seen in the British Statutes at Large 1765. The Annexe to the Act includes the definition: "Easter-day (on which the rest depend) is always the first Sunday after the Full Moon, which happens upon, or next after the Twenty-first Day of March. And if the Full Moon happens upon a Sunday, Easter-day is the Sunday after." The Annexe subsequently uses the terms "Paschal Full Moon" and "Ecclesiastical Full Moon", making it clear that they approximate to the real Full Moon.
The method is quite distinct from that described above in Gregorian calendar. For a general year, one first determines the Golden Number
Golden numbers
A golden number is a number assigned to each year in sequence to indicate the year's position in a 19-year Metonic cycle. They are used in the computus and also in the Runic calendar. The golden number of any Julian or Gregorian calendar year can be calculated by dividing the year by 19, taking...
, then one uses three Tables to determine the Sunday Letter
Dominical letter
Dominical letters are letters A, B, C, D, E, F and G assigned to days in a cycle of seven with the letter A always set against 1 January as an aid for finding the day of the week of a given calendar date and in calculating Easter....
, a Cypher, and the date of the Paschal Full Moon
Paschal Full Moon
Notionally, the paschal full moon refers to the ecclesiastical full moon of the northern spring used in the determination of the date of Easter. The name "paschal" is derived from "Pascha", a transliteration of the Greek word, which is itself a transliteration of the Hebrew pesach, both words...
, from which the date of Easter Sunday follows. The Epact does not explicitly appear. Simpler tables can be used for limited periods (such as 1900-2199) during which the Cypher (which represents the effect of the Solar and Lunar corrections) does not change. Clavius' details were employed in the construction of the method, but they play no subsequent part in its use.
J R Stockton shows his derivation of an efficient computer algorithm traceable to the Tables in the Prayer Book and the Calendar Act (assuming that a description of how to use the Tables is at hand), and verifies its processes by computing matching Tables.
Julian calendar

Metonic cycle
In astronomy and calendar studies, the Metonic cycle or Enneadecaeteris is a period of very close to 19 years which is remarkable for being very nearly a common multiple of the solar year and the synodic month...
in combination with the Julian calendar
Julian calendar
The Julian calendar began in 45 BC as a reform of the Roman calendar by Julius Caesar. It was chosen after consultation with the astronomer Sosigenes of Alexandria and was probably designed to approximate the tropical year .The Julian calendar has a regular year of 365 days divided into 12 months...
. In terms of the method of the epact
Epact
The epact was originally defined as the age of the moon in days on January 1, and occurs primarily in connection with tabular methods for determining the date of Easter...
s discussed above, it effectively used a single epact table starting with an epact of 0, which was never corrected. In this case, the epact was counted on 22 March, the earliest acceptable date for Easter. This repeats every 19 years, so there are only 19 possible dates for the Paschal Full Moon from 21 March to 18 April inclusive.
Because there are no corrections as there are for the Gregorian calendar, the ecclesiastical full moon drifts away from the true full moon by more than three days every millennium, and is already a few days later. As a result, the Eastern churches celebrate Easter one week later than the Western churches about 50% of the time. (The Eastern Easter is often four or five weeks later because the Julian 20 March is 13 days later than the Gregorian 20 March for years 1900 to 2099.)
The sequence number of a year in the 19-year cycle is called its Golden Number. This term was first used in the computistic poem Massa Compoti by Alexander de Villa Dei in 1200. A later scribe added the Golden Number to tables originally composed by Abbo of Fleury
Abbo of Fleury
Abbo of Fleury , also known as Abbon or Saint Abbo was a monk, and later abbot, of the Benedictine monastery of Fleury sur Loire near Orléans, France....
in 988.
The claim by the Roman Catholic Church
Roman Catholic Church
The Catholic Church, also known as the Roman Catholic Church, is the world's largest Christian church, with over a billion members. Led by the Pope, it defines its mission as spreading the gospel of Jesus Christ, administering the sacraments and exercising charity...
in the 1582 papal bull
Papal bull
A Papal bull is a particular type of letters patent or charter issued by a Pope of the Catholic Church. It is named after the bulla that was appended to the end in order to authenticate it....
Inter gravissimas
Inter gravissimas
Inter gravissimas was a papal bull issued by Pope Gregory XIII on February 24, 1582. The document reformed the Julian calendar and created a new calendar which came to be called the Gregorian calendar, which is used in most countries today.-Description:...
, which promulgated the Gregorian calendar
Gregorian calendar
The Gregorian calendar, also known as the Western calendar, or Christian calendar, is the internationally accepted civil calendar. It was introduced by Pope Gregory XIII, after whom the calendar was named, by a decree signed on 24 February 1582, a papal bull known by its opening words Inter...
, that it restored "the celebration of Easter according to the rules fixed by ... the great ecumenical council of Nicæa" was based on a false claim by Dionysius Exiguus
Dionysius Exiguus
Dionysius Exiguus was a 6th-century monk born in Scythia Minor, modern Dobruja shared by Romania and Bulgaria. He was a member of the Scythian monks community concentrated in Tomis, the major city of Scythia Minor...
(525) that "we determine the date of Easter Day ... in accordance with the proposal agreed upon by the 318 Fathers of the Church at the Council in Nicaea." The First Council of Nicaea
First Council of Nicaea
The First Council of Nicaea was a council of Christian bishops convened in Nicaea in Bithynia by the Roman Emperor Constantine I in AD 325...
(325) only stated that Easter was to be celebrated by all Christians on the same Sunday—it did not fix any rules to determine which Sunday. The medieval computus was based on the Alexandrian computus, which was developed by the Church of Alexandria during the first decade of the 4th century using the Alexandrian calendar. The Eastern Roman Empire accepted it shortly after 380 after converting the computus to the Julian calendar
Julian calendar
The Julian calendar began in 45 BC as a reform of the Roman calendar by Julius Caesar. It was chosen after consultation with the astronomer Sosigenes of Alexandria and was probably designed to approximate the tropical year .The Julian calendar has a regular year of 365 days divided into 12 months...
. Rome accepted it sometime between the sixth and 9th centuries. The British Isles accepted it during the 7th century except for a few monasteries. Francia (all of Western Europe except Scandinavia (pagan), the British Isles, the Iberian peninsula
Iberian Peninsula
The Iberian Peninsula , sometimes called Iberia, is located in the extreme southwest of Europe and includes the modern-day sovereign states of Spain, Portugal and Andorra, as well as the British Overseas Territory of Gibraltar...
, and southern Italy) accepted it during the last quarter of the 8th century. The last Celtic monastery
Celtic Christianity
Celtic Christianity or Insular Christianity refers broadly to certain features of Christianity that were common, or held to be common, across the Celtic-speaking world during the Early Middle Ages...
to accept it, Iona
Iona Abbey
Iona Abbey is located on the Isle of Iona, just off the Isle of Mull on the West Coast of Scotland. It is one of the oldest and most important religious centres in Western Europe. The abbey was a focal point for the spread of Christianity throughout Scotland and marks the foundation of a monastic...
, did so in 716, whereas the last English monastery to accept it did so in 931. Before these dates other methods were used which resulted in dates for Easter Sunday that sometimes differed by up to five weeks.
This is the table of Paschal Full Moon dates for all Julian years since 931:
| Golden Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Paschal Full Moon date | 5A | 25M | 13A | 2A | 22M | 10A | 30M | 18A | 7A | 27M | 15A | 4A | 24M | 12A | 1A | 21M | 9A | 29M | 17A |
(M=March, A=April)
Easter day is the first Sunday after these dates.
So for a given date of the ecclesiastical full moon, there are seven possible Easter dates. The cycle of Sunday letters, however, does not repeat in seven years: because of the interruptions of the leap day every four years, the full cycle in which weekdays recur in the calendar in the same way, is 4 × 7 = 28 years, the so-called solar cycle. So the Easter dates repeated in the same order after 4 × 7 × 19 = 532 years. This Paschal cycle is also called the Victorian cycle, after Victorius of Aquitaine
Victorius of Aquitaine
Victorius of Aquitaine, a countryman of Prosper of Aquitaine and also working in Rome, produced in 457 an Easter Cycle, which was based on the consular list provided by Prosper's Chronicle. This dependency caused scholars to think that Prosper had been working on his own Easter Annals for quite...
, who introduced it in Rome in 457. It is first known to have been used by Annianus of Alexandria
Annianus of Alexandria
Annianus of Alexandria or Annianos was a monk who flourished in Alexandria during the bishopric of Theophilus of Alexandria around the beginning of the fifth century...
at the beginning of the 5th century. It has also sometimes erroneously been called the Dionysian cycle, after Dionysius Exiguus
Dionysius Exiguus
Dionysius Exiguus was a 6th-century monk born in Scythia Minor, modern Dobruja shared by Romania and Bulgaria. He was a member of the Scythian monks community concentrated in Tomis, the major city of Scythia Minor...
, who prepared Easter tables that started in 532; but he apparently did not realize that the Alexandrian computus which he described had a 532-year cycle, although he did realize that his 95-year table was not a true cycle. Venerable Bede
Bede
Bede , also referred to as Saint Bede or the Venerable Bede , was a monk at the Northumbrian monastery of Saint Peter at Monkwearmouth, today part of Sunderland, England, and of its companion monastery, Saint Paul's, in modern Jarrow , both in the Kingdom of Northumbria...
(7th century) seems to have been the first to identify the solar cycle and explain the Paschal cycle from the Metonic cycle and the solar cycle.
In medieval western Europe, the dates of the Paschal Full Moon (14 Nisan) given above could be memorized with the help of a 19-line alliterative poem in Latin:
Nonae Aprilis norunt quinos V octonae kalendae assim depromunt. I Idus Aprilis etiam sexis, VI nonae quaternae namque dipondio. II Item undene ambiunt quinos, V quatuor idus capiunt ternos. III Ternas kalendas titulant seni, VI quatuor dene cubant in quadris. IIII Septenas idus septem eligunt, VII senae kalendae sortiunt ternos, III denis septenis donant assim. I Pridie nonas porro quaternis, IIII nonae kalendae notantur septenis. VII Pridie idus panditur quinis, V kalendas Aprilis exprimunt unus. I Duodene namque docte quaternis, IIII speciem quintam speramus duobus. II Quaternae kalendae quinque coniciunt, V quindene constant tribus adeptis. III
The first half-line of each line gives the date of the Paschal Full Moon from the table above for each year in the 19-year cycle. The second half-line gives the ferial regular, or weekday displacement, of the day of that year's Paschal Full Moon from the concurrent, or the weekday of 24 March. The ferial regular is repeated in Roman numerals in the third column.
Note on Operations
When expressing Easter algorithms without using Tables, it has been customary to employ only the integer operations additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
, modulo
Modulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
, and assignment
Assignment (computer science)
In computer programming, an assignment statement sets or re-sets the value stored in the storage location denoted by a variable name. In most imperative computer programming languages, assignment statements are one of the basic statements...
(plus minus times div mod assign). That is compatible with the use of simple mechanical or electronic calculators. But it is an undesirable restriction for computer programming, where conditional operators and statements, as well as look-up tables, are always available. One can easily see how conversion from Day-of-March (22 to 56) to Day-and-Month (22 March to 25 April) can be done as
(if DoM>31) {Day=DoM-31, Month=Apr} else {Day=DoM, Month=Mar}.
More importantly, using such conditionals also simplifies the core of the Gregorian calculation.
Gauss algorithm
The mathematician Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
presented this algorithm for calculating the date of the Julian or Gregorian Easter in 1800 except for one step that he corrected in 1816. In 1800 he incorrectly stated . In 1807 he replaced the condition with the simpler . In 1811 he limited his algorithm to the 18th and 19th centuries only, and stated that 26 April is always replaced with 19 April and 25 April by 18 April. In 1816 he thanked his student Peter Paul Tittel for pointing out that p was wrong in 1800.
| Expression | | year = 1777 |
|---|---|
| a = year mod Modulo operation In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n... 19 |
a = 10 |
| b = year mod 4 | b = 1 |
| c = year mod 7 | c = 6 |
| k = floor (year/100) | k = 17 |
| p = floor ((13 + 8k)/25) | p = 5 |
| q = floor (k/4) | q = 4 |
| M = (15 − p + k − q) mod 30 | M = 23 |
| N = (4 + k − q) mod 7 | N = 3 |
| d = (19a + M) mod 30 | d = 3 |
| e = (2b + 4c + 6d + N) mod 7 | e = 5 |
| Gregorian Easter is 22 + d + e March or d + e − 9 April | 30 March |
| if d = 29 and e = 6, replace 26 April with 19 April | |
| if d = 28, e = 6, and (11M + 11) mod 30 < 19, replace 25 April with 18 April | |
| For the Julian Easter in the Julian calendar M = 15 and N = 6 (k, p, and q are unnecessary) | |
Anonymous Gregorian algorithm
"A New York correspondent" submitted this algorithm for determining the Gregorian Easter to the journal NatureNature (journal)
Nature, first published on 4 November 1869, is ranked the world's most cited interdisciplinary scientific journal by the Science Edition of the 2010 Journal Citation Reports...
in 1876. It has been reprinted many times, in 1877 by Samuel Butcher in The Ecclesiastical Calendar, in 1922 by H. Spencer Jones
Harold Spencer Jones
Sir Harold Spencer Jones KBE FRS was an English astronomer. Although born "Jones", his surname became "Spencer Jones"....
in General Astronomy, in 1977 by the Journal of the British Astronomical Association, in 1977 by The Old Farmer's Almanac
Old Farmer's Almanac
The Old Farmer's Almanac is a reference book that contains weather forecasts, tide tables, planting charts, astronomical data, recipes, and articles on a number of topics including gardening, sports, astronomy and farming...
, in 1988 by Peter Duffett-Smith in Practical Astronomy with your Calculator
Practical Astronomy with your Calculator
Practical Astronomy with your Calculator is a book written by Peter Duffett-Smith, a University Lecturer and a Fellow of Downing College. It was first published in 1979 and has been reprinted for over 30 years. The book teaches how to solve astronomical calculations with a pocket calculator...
, and in 1991 by Jean Meeus
Jean Meeus
Jean Meeus is a Belgian astronomer specializing in celestial mechanics. The asteroid 2213 Meeus is named after him.Jean Meeus studied mathematics at the University of Leuven in Belgium, where he received the Degree of Licentiate in 1953...
in Astronomical Algorithms.
| Expression | Y = 1961 | Y = 2009 |
|---|---|---|
| a = Y mod Modulo operation In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n... 19 |
a = 4 | a = 14 |
| b = floor (Y / 100) | b = 19 | b = 20 |
| c = Y mod 100 | c = 61 | c = 9 |
| d = floor (b / 4) | d = 4 | d = 5 |
| e = b mod 4 | e = 3 | e = 0 |
| f = floor ((b + 8) / 25) | f = 1 | f = 1 |
| g = floor ((b − f + 1) / 3) | g = 6 | g = 6 |
| h = (19a + b − d − g + 15) mod 30 | h = 10 | h = 20 |
| i = floor (c / 4) | i = 15 | i = 2 |
| k = c mod 4 | k = 1 | k = 1 |
| L = (32 + 2e + 2i − h − k) mod 7 | L = 1 | L = 1 |
| m = floor ((a + 11h + 22L) / 451) | m = 0 | m = 0 |
| month = floor ((h + L − 7m + 114) / 31) | month = 4 (April) | month = 4 (April) |
| day = ((h + L − 7m + 114) mod 31) + 1 | day = 2 | day = 12 |
| Gregorian Easter | 2 April 1961 | 12 April 2009 |
Meeus Julian algorithm
Jean MeeusJean Meeus
Jean Meeus is a Belgian astronomer specializing in celestial mechanics. The asteroid 2213 Meeus is named after him.Jean Meeus studied mathematics at the University of Leuven in Belgium, where he received the Degree of Licentiate in 1953...
, in his book Astronomical Algorithms (1991, p. 69), presents the following algorithm for calculating the Julian Easter in the Julian calendar. This is not the Gregorian Easter now used by Western churches. To obtain the Eastern Orthodox Easter normally given in the Gregorian calendar, 13 days must be added to these Julian Easter dates between 1900 and 2099 inclusive as shown.
| Expression | Y = 2008 | Y = 2009 | Y = 2010 | Y = 2011 |
|---|---|---|---|---|
| a = Y mod Modulo operation In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n... 4 |
a = 0 | a = 1 | a = 2 | a = 3 |
| b = Y mod 7 | b = 6 | b = 0 | b = 1 | b = 2 |
| c = Y mod 19 | c = 13 | c = 14 | c = 15 | c = 16 |
| d = (19c + 15) mod 30 | d = 22 | d = 11 | d = 0 | d = 19 |
| e = (2a + 4b − d + 34) mod 7 | e = 1 | e = 4 | e = 0 | e = 1 |
| month = floor ((d + e + 114) / 31) | 4 (April) | 4 (April) | 3 (March) | 4 (April) |
| day = ((d + e + 114) mod 31) + 1 | 14 | 6 | 22 | 11 |
| Easter Day (Julian calendar) | 14 April 2008 | 6 April 2009 | 22 March 2010 | 11 April 2011 |
| Easter Day (Gregorian calendar) | 27 April 2008 | 19 April 2009 | 4 April 2010 | 24 April 2011 |
Software
- Perl - Rich Bowen's Date::Easter module available from CPANCPANCPAN, the Comprehensive Perl Archive Network, is an archive of nearly 100,000 modules of software written in Perl, as well as documentation for it. It has a presence on the World Wide Web at and is mirrored worldwide at more than 200 locations...
. - Excel =DOLLAR(("4/"&A1)/7+MOD(19*MOD(A1,19)-7,30)*14%,)*7-6, where the year is contained in cell A1.
- Excel =ROUND(DATE(A1,4,1)/7+MOD(19*MOD(A1,19)-7,30)*14%,0)*7-6, the same as above but system local settings independent
See also
- Christian Zeller
- Crucifixion darkness and eclipse
- Reform of the date of EasterReform of the date of EasterReform of the date of Easter has been proposed several times because the current system for determining the date of Easter is seen as presenting two significant problems:...
Further reading
- Mosshammer, Alden A. The Easter Computus and the Origins of the Christian Era. Oxford: Oxford University Press, 2008. ISBN 0-19-954312-7.
External links
- The Complete Works of Venerable Bede Vol. 6 (Contains De Temporibus and De Temporum Ratione.)
- The entry on epacts in the Catholic Encyclopedia of 1911
- The original texts of the Gregorian calendar reform (in Latin), with translations into French by Rodolphe Audette
- An Easter calculator with an extensive bibliography, and with useful links
- Ephemeris site of the Bureau des Longitudes with an Easter calculator
- A calendar page and calculator by Holger Oertel
- A page from Clive Feather with a brief explanation, some more tables, and another algorithm An extensive calendar site (auf Deutsch) and calendar and Easter calculator by Nikolaus A. Bär
- Explanation of the Gregorian solar and lunar calendar, with improved procedures over the tabular method, by David Madore
- Gregorian Lunar Calendar: A table of the Gregorian New Moons for 1900-2199
- A table of Gregorian New Moons for the years 1700-1899, from the same source
- A similar table for the years 2200-2299
- A calendar dividing the Gregorian lunar year 2003 into 30-day and 29-day lunar months
- A discussion of the Nicene Council's Easter decision and of how some commentators exaggerate the scope of the Council's decision
- Improved algorithm by Dr. Heiner Lichtenberg (in German) (in English)
- Dionysius Exiguus' Easter table
- Mnemonic Computus Diagrams of Hands from manuscript in The British Library
- St. Gallen, Stiftsbibliothek, Codex Sangallensis 378 (11th century) p. 28. Contains the poem Nonae Aprilis norunt quinos.
- Towards a Common Date for Easter World Council of ChurchesWorld Council of ChurchesThe World Council of Churches is a worldwide fellowship of 349 global, regional and sub-regional, national and local churches seeking unity, a common witness and Christian service. It is a Christian ecumenical organization that is based in the Ecumenical Centre in Geneva, Switzerland...
(Faith and Order) and Middle East Council of Churches consultation; Aleppo, Syria; 5–10 March 1997 - A simple method for determining the date of Easter for all years 326 to 4099 A.D. by Ronald W. Mallen
- Text of the Calendar (New Style) Act 1750, British Act of Parliament introducing the Gregorian Calendar as amended to date. Contains tables for calculating Easter up until the year 8599. Contrast with the Act as passed.
- About the Greek Easter and Greek Easter calculator An Orthodox Easter calculator with technical discussion and full source code listing (javascript)

