Finite ring
Encyclopedia
In mathematics
, more specifically abstract algebra
, a finite ring is a ring
(not necessarily with a multiplicative identity) that has a finite number of elements.
Every finite field
is an example of a finite ring, and the additive part of every finite ring is an example of an abelian
finite group
, but the concept of finite rings in their own right has a more recent history.
proposed the following problem in the American Mathematical Monthly
: "(1) What is the order of the smallest non-trivial ring with identity which is not a field? Find two such rings with this minimal order. Are there more? (2) How many rings of order four are there?"
One can find the solution by D.M. Bloom in a two-page proof (71:919–20) that there are eleven rings of order 4, three of which have a multiplicative identity. Indeed, four-element rings introduce the complexity of the subject. There are three rings over the cyclic group
C4 and eight rings over the Klein four-group
. There is an interesting display of the discriminatory tools (nilpotent
s, zero-divisors, idempotents, and left- and right-identities) in Gregory Dresden's lecture notes (see reference).
The occasion of non-commutativity in finite rings was described in 1968 in the same journal (75:512–14) by K. Eldrige in two theorems: If the order m of a finite ring with 1 has a cube-free factorization, then it is commutative
. And if a non-commutative finite ring with 1 has the order of a prime cubed, then the ring is isomorphic to the upper triangular 2 × 2 matrix ring over the Galois field of the prime.
The study of rings of order the cube of a prime was further developed by R. Raghavendra in 1969 (Compositio Mathematica 21:195–229). In 1973 the Proceedings of the Japan Academy 49:795–9 published Robert Gilmer and Joe Mott’s paper "Associative rings of order p3". Next Flor and Wessenbauer (1975) made improvements on the cube-of-a-prime case. Definitive work on the isomorphism classes came with V.G. Antipkin and V.P Elizarov (1982) writing in the Siberian Mathematical Journal (23:457–64). They prove that for p > 2, the number of classes is 3p + 50.
There are earlier references in the topic of finite rings, such as Robert Ballieu (1947) "Anneaux finis" in Ann. Soc. Sci Bruxelles (61:222–227). Earlier work by Scorza (1935) is noted by Irving Kaplansky
in his review (MR0022841) of Ballieu.
These are a few of the facts that are known about the number of finite rings of a given order (suppose p and q represent distinct prime numbers):
The number of rings with n elements is listed under A027623 in the On-Line Encyclopedia of Integer Sequences
.
, asserts that any finite division ring
is necessarily commutative (and therefore a finite field
). Nathan Jacobson
later discovered yet another condition which guarantees commutativity of a ring:
If for every element r of R there exists an integer such that , then R is commutative.
If, r2 = r for every r, the ring is called a Boolean ring
. More general conditions which guarantee commutativity of a ring are also known.
Yet another theorem by Wedderburn has, as its consequence, a result demonstrating that the theory of finite simple ring
s is relatively straightforward in nature. More specifically, any finite simple ring is isomorphic to the ring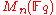
of n by n matrices over a finite field of order q. This follows from two theorems of Joseph Wedderburn
established in 1905 and 1907 (one of which is Wedderburn's little theorem). On the other hand, the classification of finite simple groups
was one of the major breakthroughs of twentieth century mathematics, its proof spanning thousands of journal pages. Therefore, in some respects, the theory of finite rings is simpler than that of finite groups.
, Galois theory
and number theory
. An important, but fairly old aspect of the theory is the classification of finite fields :
Despite the classification, finite fields are still an active area of research, including recent results on the Kakeya conjecture and open problems regarding the size of smallest primitive root
s (in number theory).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a finite ring is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
(not necessarily with a multiplicative identity) that has a finite number of elements.
Every finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
is an example of a finite ring, and the additive part of every finite ring is an example of an abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
, but the concept of finite rings in their own right has a more recent history.
Enumeration
In 1964 David SingmasterDavid Singmaster
David Breyer Singmaster is a retired professor of mathematics at London South Bank University, England, UK. A self-described metagrobologist, he is most famous for his solution to the Rubik's cube and his huge personal collection of mechanical puzzles and books of brain teasers. He is also...
proposed the following problem in the American Mathematical Monthly
American Mathematical Monthly
The American Mathematical Monthly is a mathematical journal founded by Benjamin Finkel in 1894. It is currently published 10 times each year by the Mathematical Association of America....
: "(1) What is the order of the smallest non-trivial ring with identity which is not a field? Find two such rings with this minimal order. Are there more? (2) How many rings of order four are there?"
One can find the solution by D.M. Bloom in a two-page proof (71:919–20) that there are eleven rings of order 4, three of which have a multiplicative identity. Indeed, four-element rings introduce the complexity of the subject. There are three rings over the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
C4 and eight rings over the Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
. There is an interesting display of the discriminatory tools (nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
s, zero-divisors, idempotents, and left- and right-identities) in Gregory Dresden's lecture notes (see reference).
The occasion of non-commutativity in finite rings was described in 1968 in the same journal (75:512–14) by K. Eldrige in two theorems: If the order m of a finite ring with 1 has a cube-free factorization, then it is commutative
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. And if a non-commutative finite ring with 1 has the order of a prime cubed, then the ring is isomorphic to the upper triangular 2 × 2 matrix ring over the Galois field of the prime.
The study of rings of order the cube of a prime was further developed by R. Raghavendra in 1969 (Compositio Mathematica 21:195–229). In 1973 the Proceedings of the Japan Academy 49:795–9 published Robert Gilmer and Joe Mott’s paper "Associative rings of order p3". Next Flor and Wessenbauer (1975) made improvements on the cube-of-a-prime case. Definitive work on the isomorphism classes came with V.G. Antipkin and V.P Elizarov (1982) writing in the Siberian Mathematical Journal (23:457–64). They prove that for p > 2, the number of classes is 3p + 50.
There are earlier references in the topic of finite rings, such as Robert Ballieu (1947) "Anneaux finis" in Ann. Soc. Sci Bruxelles (61:222–227). Earlier work by Scorza (1935) is noted by Irving Kaplansky
Irving Kaplansky
Irving Kaplansky was a Canadian mathematician.-Biography:He was born in Toronto, Ontario, Canada, after his parents emigrated from Poland and attended the University of Toronto as an undergraduate. After receiving his Ph.D...
in his review (MR0022841) of Ballieu.
These are a few of the facts that are known about the number of finite rings of a given order (suppose p and q represent distinct prime numbers):
- There are two finite rings of order p.
- There are four finite rings of order pq.
- There are eleven finite rings of order p2.
- There are twenty-two finite rings of order p2q.
- There are fifty-two finite rings of order eight.
- There are 3p + 50 finite rings of order p3, p > 2.
The number of rings with n elements is listed under A027623 in the On-Line Encyclopedia of Integer Sequences
On-Line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...
.
Wedderburn's theorems
There are other deep aspects to the theory of finite rings, apart from mere enumeration. For instance, a remarkable theorem by Joseph Wedderburn, known as Wedderburn's little theoremWedderburn's little theorem
In mathematics, Wedderburn's little theorem states that every finite domain is a field. In other words, for finite rings, there is no distinction between domains, skew-fields and fields.The Artin–Zorn theorem generalizes the theorem to alternative rings....
, asserts that any finite division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
is necessarily commutative (and therefore a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
). Nathan Jacobson
Nathan Jacobson
Nathan Jacobson was an American mathematician....
later discovered yet another condition which guarantees commutativity of a ring:
If for every element r of R there exists an integer such that , then R is commutative.
If, r2 = r for every r, the ring is called a Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
. More general conditions which guarantee commutativity of a ring are also known.
Yet another theorem by Wedderburn has, as its consequence, a result demonstrating that the theory of finite simple ring
Simple ring
In abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
s is relatively straightforward in nature. More specifically, any finite simple ring is isomorphic to the ring
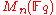of n by n matrices over a finite field of order q. This follows from two theorems of Joseph WedderburnJoseph Wedderburn
Joseph Henry Maclagan Wedderburn was a Scottish mathematician, who taught at Princeton University for most of his career. A significant algebraist, he proved that a finite division algebra is a field, and part of the Artin–Wedderburn theorem on simple algebras...
established in 1905 and 1907 (one of which is Wedderburn's little theorem). On the other hand, the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
was one of the major breakthroughs of twentieth century mathematics, its proof spanning thousands of journal pages. Therefore, in some respects, the theory of finite rings is simpler than that of finite groups.
Finite field
The theory of finite fields is perhaps the most important aspect of finite ring theory due to its intimate connections with algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. An important, but fairly old aspect of the theory is the classification of finite fields :
- The order or number of elements of a finite field equals pn, where p is a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
called the characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of the field, and n is a positive integer. - For every prime number p and positive integer n, there exists a finite field with pn elements.
- Any two finite fields with the same order are isomorphic.
Despite the classification, finite fields are still an active area of research, including recent results on the Kakeya conjecture and open problems regarding the size of smallest primitive root
Primitive root modulo n
In modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
s (in number theory).