
Centrality
Encyclopedia
Within graph theory
and network analysis
, there are various measures of the centrality of a vertex
within a graph
that determine the relative importance of a vertex within the graph (for example, how important a person is within a social network
, or, in the theory of space syntax
, how important a room is within a building or how well-used a road is within an urban network). Many of the centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological
origin.
There are four measures of centrality that are widely used in network analysis: degree centrality, betweenness, closeness, and eigenvector centrality. For a review as well as generalizations to weighted networks, see Opsahl et al. (2010).
For a graph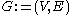 with n vertices, the degree centrality
with n vertices, the degree centrality 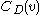 for vertex
for vertex  is:
is:
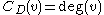
Calculating degree centrality for all nodes in a graph takes
in a graph takes  in a dense adjacency matrix
in a dense adjacency matrix
representation of the graph, and for edges in a graph takes
in a graph takes 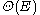 in a sparse matrix
in a sparse matrix
representation.
The definition of centrality on the node level can be extended to the whole graph. Let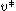 be the node with highest degree centrality in
be the node with highest degree centrality in  . Let
. Let 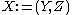 be the
be the  node connected graph that maximizes the following quantity (with
node connected graph that maximizes the following quantity (with 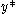 being the node with highest degree centrality in
being the node with highest degree centrality in 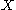 ):
):
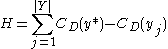
Then the degree centrality of the graph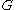 is defined as follows:
is defined as follows:
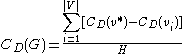
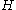 is maximized when the graph
is maximized when the graph 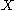 contains one node that is connected to all other nodes and all other nodes are connected only to this one central node (a star graph). In this case
contains one node that is connected to all other nodes and all other nodes are connected only to this one central node (a star graph). In this case
so the degree centrality of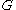 reduces to:
reduces to: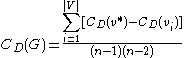
within a graph
(there is also edge betweenness, which is not discussed here). It was introduced as a measure for quantifying the control of a human on the communication between other humans in a social network by Linton Freeman. In his conception, vertices that have a high probability to occur on a randomly chosen shortest path
between two randomly chosen nodes have a high betweenness.
For a graph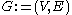 with n vertices, the betweenness
with n vertices, the betweenness 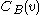 for vertex
for vertex  is computed as follows:
is computed as follows:
1. For each pair of vertices (s,t), compute all shortest paths
between them.
2. For each pair of vertices (s,t), determine the fraction of shortest paths that pass through the vertex in question (here, vertex v).
3. Sum this fraction over all pairs of vertices (s,t).
Or, more succinctly:
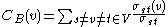
where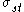 is the number of shortest paths from s to t, and
is the number of shortest paths from s to t, and  is the number of shortest paths from s to t that pass through a vertex v. This may be normalised by dividing through the number of pairs of vertices not including v, which is
is the number of shortest paths from s to t that pass through a vertex v. This may be normalised by dividing through the number of pairs of vertices not including v, which is 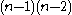 for directed graphs and
for directed graphs and 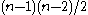 for undirected graphs. For example, in an undirected star graph
for undirected graphs. For example, in an undirected star graph
, the center vertex (which is contained in every possible shortest path) would have a betweenness of (1, if normalised) while the leaves (which are contained in no shortest paths) would have a betweenness of 0.
(1, if normalised) while the leaves (which are contained in no shortest paths) would have a betweenness of 0.
Calculating the betweenness and closeness centralities of all the vertices in a graph involves calculating the shortest paths between all pairs of vertices on a graph. This takes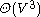 time with the Floyd–Warshall algorithm, modified to not only find one but count all shortest paths between two nodes. On a sparse graph, Johnson's algorithm
time with the Floyd–Warshall algorithm, modified to not only find one but count all shortest paths between two nodes. On a sparse graph, Johnson's algorithm
may be more efficient, taking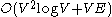
time. On unweighted graphs, calculating betweenness centrality takes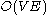
time using Brandes' algorithm.
In calculating betweenness and closeness centralities of all vertices in a graph, it is assumed that graphs are undirected and connected with the allowance of loops and multiple edges. When specifically dealing with network graphs, oftentimes graphs are without loops or multiple edges to maintain simple relationships (where edges represent connections between two people or vertices). In this case, using Brandes' algorithm will divide final centrality scores by 2 to account for each shortest path being counted twice.
there is a natural distance metric between all pairs of nodes, defined by the length of their shortest paths
. The farness of a node s is defined as the sum of its distances to all other nodes, and its closeness is defined as the inverse of the farness. Thus, a node is the more central the lower its total distance to all other nodes. Closeness can be regarded as a measure of how long it will take to spread information from s to all other nodes sequentially.
In the classic definition of the closeness centrality, the spread of information is modeled by the use of shortest paths. This model might not be the most realistic for all types of communication scenarios. Thus, related definitions have been discussed to measure closeness, like the random-walk centrality introduced by Noh and Rieger (2004). It measures the speed with which randomly walking messages reach a vertex from elsewhere in the network—a sort of random-walk version of closeness centrality.
The information centrality of Stephenson and Zelen (1989) is another closeness measure, which bears some similarity to that of Noh and Rieger. In essence it measures the harmonic mean length of paths ending at a vertex i, which is smaller if i has many short paths connecting it to other vertices.
Note that by definition of graph theoretic distances, the classic closeness centrality of all nodes in an unconnected graph would be 0.
Dangalchev (2006), in order to measure the network vulnerability, modifies the definition for closeness such that can be used for disconnected graphs and the total closeness is easier to calculate: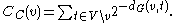
Another extension to networks with disconnected components has been proposed by Opsahl (2010).
in a network. It assigns relative scores to all nodes in the network based on the principle that connections to high-scoring nodes contribute more to the score of the node in question than equal connections to low-scoring nodes. Google
's PageRank
is a variant of the Eigenvector centrality measure. Another related centrality is Katz centrality
.
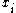 denote the score of the
denote the score of the 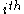 node. Let
node. Let 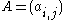 be the adjacency matrix
be the adjacency matrix
of the network. Hence if the
if the  node is linked to the
node is linked to the 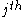 node, and
node, and 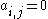 otherwise. More generally, the entries in A can be real numbers representing connection strengths, as in a stochastic matrix
otherwise. More generally, the entries in A can be real numbers representing connection strengths, as in a stochastic matrix
.
For the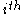 node, let the centrality score be proportional to the sum of the scores of all nodes which are connected to it. Hence
node, let the centrality score be proportional to the sum of the scores of all nodes which are connected to it. Hence
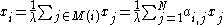
where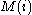 is the set of nodes that are connected to the
is the set of nodes that are connected to the 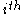 node, N is the total number of nodes and
node, N is the total number of nodes and 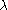 is a constant. In vector notation this can be rewritten as
is a constant. In vector notation this can be rewritten as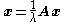 , or as the eigenvector equation
, or as the eigenvector equation 
In general, there will be many different eigenvalues for which an eigenvector solution exists. However, the additional requirement that all the entries in the eigenvector be positive implies (by the Perron–Frobenius theorem
for which an eigenvector solution exists. However, the additional requirement that all the entries in the eigenvector be positive implies (by the Perron–Frobenius theorem
) that only the greatest eigenvalue results in the desired centrality measure. The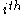 component of the related eigenvector then gives the centrality score of the
component of the related eigenvector then gives the centrality score of the 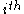 node in the network. Power iteration
node in the network. Power iteration
is one of many eigenvalue algorithm
s that may be used to find this dominant eigenvector.
A centrality index is a real-valued function on the nodes of a graph. It is a structural index, i.e., if and
and 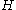 are two isomorphic
are two isomorphic
graphs and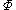 is the mapping from the vertex set
is the mapping from the vertex set 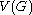 of
of 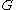 to V(H), then the centrality of a vertex
to V(H), then the centrality of a vertex  of
of 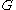 must be the same as the centrality of
must be the same as the centrality of  in
in 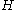 . Conventionally, the higher the centrality index of a node, the higher its perceived centrality in the graph.
. Conventionally, the higher the centrality index of a node, the higher its perceived centrality in the graph.
This definition comprises all classic centrality measures but not all measures that fulfill this definition would be accepted as centrality indices.
Borgatti and Everett summarize that centrality indices measure the position of a node along a predefined set of walks. They characterize centrality indices along four dimensions: the set of walks, whether the length or the number of these walks is considered, the position of the node on the walks (at the start=radial; in the middle=medial), and how the numbers assigned to the paths are summarized in the measure (average, median, weighted sum, ...). This leads to a characterization by the way a centrality index is calculated. In a different characterization, Borgatti differentiates the centrality indices by what type of paths they consider and which type of network flow they imply. The latter characterizes the centrality indices by the quality with which they predict which node is most central for a given network flow process. This characterization thus provides guidance on when to use which centrality index.
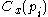 is any centrality measure of point
is any centrality measure of point  , if
, if 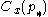 is the largest such measure in the network, and if
is the largest such measure in the network, and if 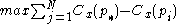 is the largest sum of differences in point centrality
is the largest sum of differences in point centrality 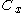 for any graph of with the same number of nodes, then the centralization of the network is:
for any graph of with the same number of nodes, then the centralization of the network is: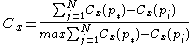
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
and network analysis
Network theory
Network theory is an area of computer science and network science and part of graph theory. It has application in many disciplines including statistical physics, particle physics, computer science, biology, economics, operations research, and sociology...
, there are various measures of the centrality of a vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
within a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
that determine the relative importance of a vertex within the graph (for example, how important a person is within a social network
Social network
A social network is a social structure made up of individuals called "nodes", which are tied by one or more specific types of interdependency, such as friendship, kinship, common interest, financial exchange, dislike, sexual relationships, or relationships of beliefs, knowledge or prestige.Social...
, or, in the theory of space syntax
Space syntax
The term space syntax encompasses a set of theories and techniques for the analysis of spatial configurations. Originally it was conceived by Bill Hillier, Julienne Hanson and colleagues at The Bartlett, University College London in the late 1970s to early 1980s as a tool to help architects...
, how important a room is within a building or how well-used a road is within an urban network). Many of the centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological
Sociology
Sociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
origin.
There are four measures of centrality that are widely used in network analysis: degree centrality, betweenness, closeness, and eigenvector centrality. For a review as well as generalizations to weighted networks, see Opsahl et al. (2010).
Degree centrality
The first, and simplest, is degree centrality. Degree centrality is defined as the number of links incident upon a node (i.e., the number of ties that a node has). Degree is often interpreted in terms of the immediate risk of a node for catching whatever is flowing through the network (such as a virus, or some information). If the network is directed (meaning that ties have direction), then we usually define two separate measures of degree centrality, namely indegree and outdegree. Indegree is a count of the number of ties directed to the node, and outdegree is the number of ties that the node directs to others. For positive relations such as friendship or advice, indegree is often interpreted as a form of popularity, and outdegree as gregariousness.For a graph
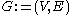 with n vertices, the degree centrality
with n vertices, the degree centrality 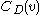 for vertex
for vertex  is:
is: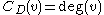
Calculating degree centrality for all nodes
 in a graph takes
in a graph takes  in a dense adjacency matrix
in a dense adjacency matrixAdjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
representation of the graph, and for edges
 in a graph takes
in a graph takes 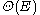 in a sparse matrix
in a sparse matrixSparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
representation.
The definition of centrality on the node level can be extended to the whole graph. Let
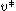 be the node with highest degree centrality in
be the node with highest degree centrality in  . Let
. Let 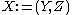 be the
be the  node connected graph that maximizes the following quantity (with
node connected graph that maximizes the following quantity (with 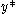 being the node with highest degree centrality in
being the node with highest degree centrality in 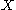 ):
):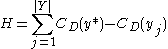
Then the degree centrality of the graph
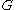 is defined as follows:
is defined as follows: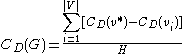
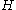 is maximized when the graph
is maximized when the graph 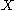 contains one node that is connected to all other nodes and all other nodes are connected only to this one central node (a star graph). In this case
contains one node that is connected to all other nodes and all other nodes are connected only to this one central node (a star graph). In this case
so the degree centrality of
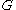 reduces to:
reduces to: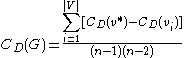
Betweenness centrality
Betweenness is a centrality measure of a vertexVertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
within a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
(there is also edge betweenness, which is not discussed here). It was introduced as a measure for quantifying the control of a human on the communication between other humans in a social network by Linton Freeman. In his conception, vertices that have a high probability to occur on a randomly chosen shortest path
Shortest path problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized...
between two randomly chosen nodes have a high betweenness.
For a graph
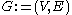 with n vertices, the betweenness
with n vertices, the betweenness 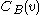 for vertex
for vertex  is computed as follows:
is computed as follows:1. For each pair of vertices (s,t), compute all shortest paths
Shortest path problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized...
between them.
2. For each pair of vertices (s,t), determine the fraction of shortest paths that pass through the vertex in question (here, vertex v).
3. Sum this fraction over all pairs of vertices (s,t).
Or, more succinctly:
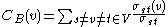
where
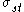 is the number of shortest paths from s to t, and
is the number of shortest paths from s to t, and  is the number of shortest paths from s to t that pass through a vertex v. This may be normalised by dividing through the number of pairs of vertices not including v, which is
is the number of shortest paths from s to t that pass through a vertex v. This may be normalised by dividing through the number of pairs of vertices not including v, which is 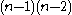 for directed graphs and
for directed graphs and 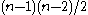 for undirected graphs. For example, in an undirected star graph
for undirected graphs. For example, in an undirected star graphStar (graph theory)
In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves...
, the center vertex (which is contained in every possible shortest path) would have a betweenness of
 (1, if normalised) while the leaves (which are contained in no shortest paths) would have a betweenness of 0.
(1, if normalised) while the leaves (which are contained in no shortest paths) would have a betweenness of 0.Calculating the betweenness and closeness centralities of all the vertices in a graph involves calculating the shortest paths between all pairs of vertices on a graph. This takes
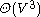 time with the Floyd–Warshall algorithm, modified to not only find one but count all shortest paths between two nodes. On a sparse graph, Johnson's algorithm
time with the Floyd–Warshall algorithm, modified to not only find one but count all shortest paths between two nodes. On a sparse graph, Johnson's algorithmJohnson's algorithm
Johnson's algorithm is a way to find the shortest paths between all pairs of vertices in a sparse directed graph. It allows some of the edge weights to be negative numbers, but no negative-weight cycles may exist...
may be more efficient, taking
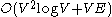
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
time. On unweighted graphs, calculating betweenness centrality takes
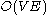
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
time using Brandes' algorithm.
In calculating betweenness and closeness centralities of all vertices in a graph, it is assumed that graphs are undirected and connected with the allowance of loops and multiple edges. When specifically dealing with network graphs, oftentimes graphs are without loops or multiple edges to maintain simple relationships (where edges represent connections between two people or vertices). In this case, using Brandes' algorithm will divide final centrality scores by 2 to account for each shortest path being counted twice.
Closeness centrality
In graphsGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
there is a natural distance metric between all pairs of nodes, defined by the length of their shortest paths
Shortest path problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized...
. The farness of a node s is defined as the sum of its distances to all other nodes, and its closeness is defined as the inverse of the farness. Thus, a node is the more central the lower its total distance to all other nodes. Closeness can be regarded as a measure of how long it will take to spread information from s to all other nodes sequentially.
In the classic definition of the closeness centrality, the spread of information is modeled by the use of shortest paths. This model might not be the most realistic for all types of communication scenarios. Thus, related definitions have been discussed to measure closeness, like the random-walk centrality introduced by Noh and Rieger (2004). It measures the speed with which randomly walking messages reach a vertex from elsewhere in the network—a sort of random-walk version of closeness centrality.
The information centrality of Stephenson and Zelen (1989) is another closeness measure, which bears some similarity to that of Noh and Rieger. In essence it measures the harmonic mean length of paths ending at a vertex i, which is smaller if i has many short paths connecting it to other vertices.
Note that by definition of graph theoretic distances, the classic closeness centrality of all nodes in an unconnected graph would be 0.
Dangalchev (2006), in order to measure the network vulnerability, modifies the definition for closeness such that can be used for disconnected graphs and the total closeness is easier to calculate:
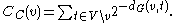
Another extension to networks with disconnected components has been proposed by Opsahl (2010).
Eigenvector centrality
Eigenvector centrality is a measure of the importance of a nodeNode (networking)
In communication networks, a node is a connection point, either a redistribution point or a communication endpoint . The definition of a node depends on the network and protocol layer referred to...
in a network. It assigns relative scores to all nodes in the network based on the principle that connections to high-scoring nodes contribute more to the score of the node in question than equal connections to low-scoring nodes. Google
Google
Google Inc. is an American multinational public corporation invested in Internet search, cloud computing, and advertising technologies. Google hosts and develops a number of Internet-based services and products, and generates profit primarily from advertising through its AdWords program...
's PageRank
PageRank
PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
is a variant of the Eigenvector centrality measure. Another related centrality is Katz centrality
Katz centrality
In Social Network Analysis there are various measures of centrality which determine the relative importance of an actor within the network. Katz centrality was introduced by Leo Katz in 1953 and is used to measure the degree of influence of an actor in a social network...
.
Using the adjacency matrix to find eigenvector centrality
Let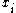 denote the score of the
denote the score of the 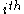 node. Let
node. Let 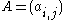 be the adjacency matrix
be the adjacency matrixAdjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of the network. Hence
 if the
if the  node is linked to the
node is linked to the 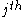 node, and
node, and 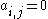 otherwise. More generally, the entries in A can be real numbers representing connection strengths, as in a stochastic matrix
otherwise. More generally, the entries in A can be real numbers representing connection strengths, as in a stochastic matrixStochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
.
For the
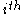 node, let the centrality score be proportional to the sum of the scores of all nodes which are connected to it. Hence
node, let the centrality score be proportional to the sum of the scores of all nodes which are connected to it. Hence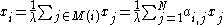
where
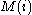 is the set of nodes that are connected to the
is the set of nodes that are connected to the 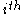 node, N is the total number of nodes and
node, N is the total number of nodes and 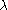 is a constant. In vector notation this can be rewritten as
is a constant. In vector notation this can be rewritten as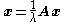 , or as the eigenvector equation
, or as the eigenvector equation 
In general, there will be many different eigenvalues
 for which an eigenvector solution exists. However, the additional requirement that all the entries in the eigenvector be positive implies (by the Perron–Frobenius theorem
for which an eigenvector solution exists. However, the additional requirement that all the entries in the eigenvector be positive implies (by the Perron–Frobenius theoremPerron–Frobenius theorem
In linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
) that only the greatest eigenvalue results in the desired centrality measure. The
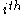 component of the related eigenvector then gives the centrality score of the
component of the related eigenvector then gives the centrality score of the 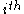 node in the network. Power iteration
node in the network. Power iterationPower iteration
In mathematics, the power iteration is an eigenvalue algorithm: given a matrix A, the algorithm will produce a number λ and a nonzero vector v , such that Av = λv....
is one of many eigenvalue algorithm
Eigenvalue algorithm
In linear algebra, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.-Characteristic polynomial:...
s that may be used to find this dominant eigenvector.
Definition and Characterization of Centrality Indices
Next to the above named classic centrality indices, there are dozens of other more specialized centrality indices. Despite its intuitive notion there is not yet a definition or characterization of centrality indices which captures all of them. A very loose definition of a centrality index is the following:A centrality index is a real-valued function on the nodes of a graph. It is a structural index, i.e., if
 and
and 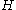 are two isomorphic
are two isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
graphs and
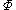 is the mapping from the vertex set
is the mapping from the vertex set 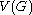 of
of 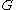 to V(H), then the centrality of a vertex
to V(H), then the centrality of a vertex  of
of 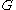 must be the same as the centrality of
must be the same as the centrality of  in
in 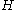 . Conventionally, the higher the centrality index of a node, the higher its perceived centrality in the graph.
. Conventionally, the higher the centrality index of a node, the higher its perceived centrality in the graph.This definition comprises all classic centrality measures but not all measures that fulfill this definition would be accepted as centrality indices.
Borgatti and Everett summarize that centrality indices measure the position of a node along a predefined set of walks. They characterize centrality indices along four dimensions: the set of walks, whether the length or the number of these walks is considered, the position of the node on the walks (at the start=radial; in the middle=medial), and how the numbers assigned to the paths are summarized in the measure (average, median, weighted sum, ...). This leads to a characterization by the way a centrality index is calculated. In a different characterization, Borgatti differentiates the centrality indices by what type of paths they consider and which type of network flow they imply. The latter characterizes the centrality indices by the quality with which they predict which node is most central for a given network flow process. This characterization thus provides guidance on when to use which centrality index.
Centralization
The centralization of any network is a measure of how central its most central node is in relation to how central all the other nodes are. The general definition of centralization for non-weighted networks was proposed by Linton Freeman (1979). Centralization measures then (a) calculate the sum in differences in centrality between the most central node in a network and all other nodes; and (b) divide this quantity by the theoretically largest such sum of differences in any network of the same degree. Thus, every centrality measure can have its own centralization measure. Defined formally, if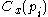 is any centrality measure of point
is any centrality measure of point  , if
, if 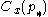 is the largest such measure in the network, and if
is the largest such measure in the network, and if 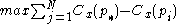 is the largest sum of differences in point centrality
is the largest sum of differences in point centrality 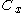 for any graph of with the same number of nodes, then the centralization of the network is:
for any graph of with the same number of nodes, then the centralization of the network is: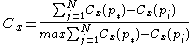
Further reading
- Freeman, L. C. (1979). Centrality in social networks: Conceptual clarification. Social Networks, 1(3), 215-239.
- Sabidussi, G. (1966). The centrality index of a graph. Psychometrika, 31 (4), 581-603.
- Freeman, L. C. (1977) A set of measures of centrality based on betweenness. Sociometry 40, 35-41.
- Koschützki, D.; Lehmann, K. A.; Peeters, L.; Richter, S.; Tenfelde-Podehl, D. and Zlotowski, O. (2005) Centrality Indices. In Brandes, U. and Erlebach, T. (Eds.) Network Analysis: Methodological Foundations, pp. 16–61, LNCS 3418, Springer-Verlag.
- Bonacich, P.(1987) Power and Centrality: A Family of Measures, The American Journal of Sociology, 92 (5), pp 1170–1182
External links
- https://networkx.lanl.gov/trac/attachment/ticket/119/page_rank.py
- http://www.faculty.ucr.edu/~hanneman/nettext/C10_Centrality.html

