
Jacobi triple product
Encyclopedia
In mathematics
, the Jacobi triple product is the mathematical identity:

for complex numbers x and y, with |x| < 1 and y ≠ 0.
It was introduced by Carl Gustav Jacob Jacobi, who proved it in 1829 in his work Fundamenta Nova Theoriae Functionum Ellipticarum.
The Jacobi triple product identity is the Macdonald identity for the affine root system of type A1, and is the Weyl denominator formula for the corresponding affine Kac–Moody algebra
.
The basis of Jacobi's proof relies on Euler's pentagonal number theorem, which is itself a specific case of the Jacobi Triple Product Identity.
Let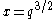 and
and  . Then we have
. Then we have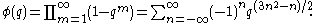
The Jacobi Triple Product also allows the Jacobi theta function to be written as an infinite product as follows:
Let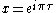 and
and 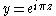 .
.
Then the Jacobi theta function

can be written in the form
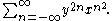
Using the Jacobi Triple Product Identity we can then write the theta function as the product
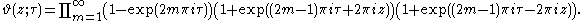
There are many different notations used to express the Jacobi triple product. It takes on a concise form when expressed in terms of q-Pochhammer symbols:
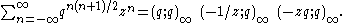
Where is the infinite q-Pochhammer symbol.
is the infinite q-Pochhammer symbol.
It enjoys a particularly elegant form when expressed in terms of the Ramanujan theta function
. For it can be written as
it can be written as

and follows the proof in Cameron (13.3) which is attributed to Richard Borcherds
. It treats the case where the power series are formal. For the analytic case, see Apostol. The Jacobi triple product identity can be expressed as
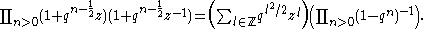
A level is a half-integer
. The vacuum state is the set of all negative levels. A state is a set of levels whose symmetric difference with the vacuum state is finite. The energy of the state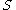 is
is
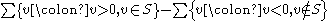
and the particle number of is
is

An unordered choice of the presence of finitely many positive levels and the absence of finitely many negative levels (relative to the vacuum) corresponds to a state, so the generating function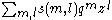 for the number
for the number 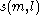 of states of energy
of states of energy  with
with 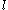 particles can be expressed as
particles can be expressed as

On the other hand, any state with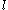 particles can be obtained from the lowest energy
particles can be obtained from the lowest energy 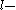 particle state,
particle state, 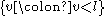 , by rearranging particles: take a partition
, by rearranging particles: take a partition  of
of  and move the top particle up by
and move the top particle up by 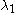 levels, the next highest particle up by
levels, the next highest particle up by 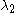 levels, etc.... The resulting state has energy
levels, etc.... The resulting state has energy  , so the generating function can also be written as
, so the generating function can also be written as
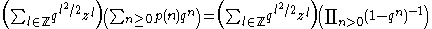
where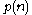 is the partition function. The uses of random partitions by Andrei Okounkov
is the partition function. The uses of random partitions by Andrei Okounkov
contains a picture of a partition exciting the vacuum.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Jacobi triple product is the mathematical identity:

for complex numbers x and y, with |x| < 1 and y ≠ 0.
It was introduced by Carl Gustav Jacob Jacobi, who proved it in 1829 in his work Fundamenta Nova Theoriae Functionum Ellipticarum.
The Jacobi triple product identity is the Macdonald identity for the affine root system of type A1, and is the Weyl denominator formula for the corresponding affine Kac–Moody algebra
Kac–Moody algebra
In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
.
The basis of Jacobi's proof relies on Euler's pentagonal number theorem, which is itself a specific case of the Jacobi Triple Product Identity.
Let
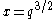 and
and  . Then we have
. Then we have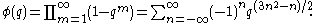
The Jacobi Triple Product also allows the Jacobi theta function to be written as an infinite product as follows:
Let
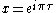 and
and 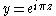 .
.Then the Jacobi theta function

can be written in the form
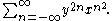
Using the Jacobi Triple Product Identity we can then write the theta function as the product
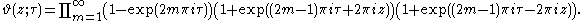
There are many different notations used to express the Jacobi triple product. It takes on a concise form when expressed in terms of q-Pochhammer symbols:
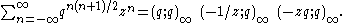
Where
 is the infinite q-Pochhammer symbol.
is the infinite q-Pochhammer symbol.It enjoys a particularly elegant form when expressed in terms of the Ramanujan theta function
Ramanujan theta function
In mathematics, particularly q-analog theory, the Ramanujan theta function generalizes the form of the Jacobi theta functions, while capturing their general properties. In particular, the Jacobi triple product takes on a particularly elegant form when written in terms of the Ramanujan theta...
. For
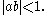 it can be written as
it can be written as
Proof
This proof uses a simplified model of the Dirac seaDirac sea
The Dirac sea is a theoretical model of the vacuum as an infinite sea of particles with negative energy. It was first postulated by the British physicist Paul Dirac in 1930 to explain the anomalous negative-energy quantum states predicted by the Dirac equation for relativistic electrons...
and follows the proof in Cameron (13.3) which is attributed to Richard Borcherds
Richard Borcherds
Richard Ewen Borcherds is a British mathematician specializing in lattices, number theory, group theory, and infinite-dimensional algebras. He was awarded the Fields Medal in 1998.- Personal life :...
. It treats the case where the power series are formal. For the analytic case, see Apostol. The Jacobi triple product identity can be expressed as
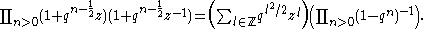
A level is a half-integer
Half-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
. The vacuum state is the set of all negative levels. A state is a set of levels whose symmetric difference with the vacuum state is finite. The energy of the state
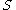 is
is
and the particle number of
 is
is
An unordered choice of the presence of finitely many positive levels and the absence of finitely many negative levels (relative to the vacuum) corresponds to a state, so the generating function
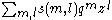 for the number
for the number 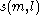 of states of energy
of states of energy  with
with 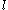 particles can be expressed as
particles can be expressed as
On the other hand, any state with
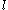 particles can be obtained from the lowest energy
particles can be obtained from the lowest energy 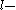 particle state,
particle state, 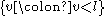 , by rearranging particles: take a partition
, by rearranging particles: take a partition  of
of  and move the top particle up by
and move the top particle up by 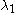 levels, the next highest particle up by
levels, the next highest particle up by 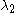 levels, etc.... The resulting state has energy
levels, etc.... The resulting state has energy  , so the generating function can also be written as
, so the generating function can also be written as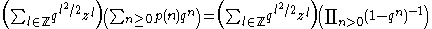
where
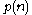 is the partition function. The uses of random partitions by Andrei Okounkov
is the partition function. The uses of random partitions by Andrei OkounkovAndrei Okounkov
Andrei Yuryevich Okounkov is a Russian mathematician who works on representation theory and its applications to algebraic geometry, mathematical physics, probability theory and special functions. He is currently a professor at Columbia University....
contains a picture of a partition exciting the vacuum.

