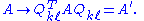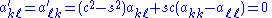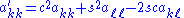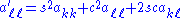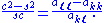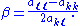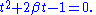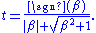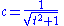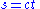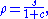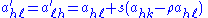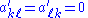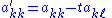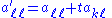Jacobi rotation
Encyclopedia
In numerical linear algebra
, a Jacobi rotation is a rotation
, Qkℓ, of a 2-dimensional linear subspace of an n-dimensional inner product space
, chosen to zero a symmetric pair of off-diagonal entries of an n×n real
symmetric matrix, A, when applied as a similarity transformation:
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
, a Jacobi rotation is a rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
, Qkℓ, of a 2-dimensional linear subspace of an n-dimensional inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, chosen to zero a symmetric pair of off-diagonal entries of an n×n real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
symmetric matrix, A, when applied as a similarity transformation:
-
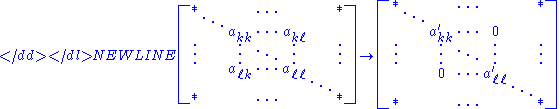
It is the core operation in the Jacobi eigenvalue algorithmJacobi eigenvalue algorithmIn numerical linear algebra, the Jacobi eigenvalue algorithm is an iterative method for the calculation of the eigenvalues and eigenvectors of a real symmetric matrix...
, which is numerically stable and well-suited to implementation on parallel processors.
Only rows k and ℓ and columns k and ℓ of A will be affected, and that A′ will remain symmetric. Also, an explicit matrix for Qkℓ is rarely computed; instead, auxiliary values are computed and A is updated in an efficient and numerically stable way. However, for reference, we may write the matrix as
-
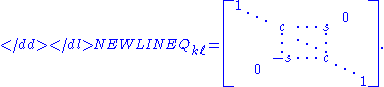
That is, Qkℓ is an identity matrix except for four entries, two on the diagonal (qkk and qℓℓ, both equal to c) and two symmetrically placed off the diagonal (qkℓ and Qℓk, equal to s and −s, respectively). Here c = cos ϑ and s = sin ϑ for some angle ϑ; but to apply the rotation, the angle itself is not required. Using Kronecker delta notation, the matrix entries can be written
-

Suppose h is an index other than k or ℓ (which must themselves be distinct). Then the similarity update produces, algebraically,
Numerically stable computation
To determine the quantities needed for the update, we must solve the off-diagonal equation for zero . This implies that
Set β to half this quantity,
If akℓ is zero we can stop without performing an update, thus we never divide by zero. Let t be tan ϑ. Then with a few trigonometric identities we reduce the equation to
For stability we choose the solution
From this we may obtain c and s as
Although we now could use the algebraic update equations given previously, it may be preferable to rewrite them. Let
so that ρ = tan(ϑ/2). Then the revised update equations are
As previously remarked, we need never explicitly compute the rotation angle ϑ. In fact, we can reproduce the symmetric update determined by Qkℓ by retaining only the three values k, ℓ, and t, with t set to zero for a null rotation. -
-
-