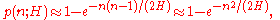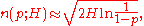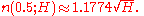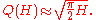Birthday attack
Encyclopedia
A birthday attack is a type of cryptographic
attack
that exploits the mathematics
behind the birthday problem in probability theory
. This attack can be used to abuse communication between two or more parties. The attack depends on the higher likelihood of collisions found between random attack attempts and a fixed degree of permutations (pigeonholes), as described in the birthday problem/paradox.
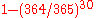 , about 7.9%. However, the probability that at least one student has the same birthday as any other student is nearly 70% (there are
, about 7.9%. However, the probability that at least one student has the same birthday as any other student is nearly 70% (there are 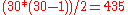 pairs of students that might match).
pairs of students that might match).
 , the goal of the attack is to find two different inputs
, the goal of the attack is to find two different inputs 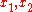 such that
such that 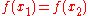 . Such a pair
. Such a pair  is called a collision. The method used to find a collision is simply to evaluate the function
is called a collision. The method used to find a collision is simply to evaluate the function  for different input values that may be chosen randomly or pseudorandomly until the same result is found more than once. Because of the birthday problem, this method can be rather efficient. Specifically, if a function
for different input values that may be chosen randomly or pseudorandomly until the same result is found more than once. Because of the birthday problem, this method can be rather efficient. Specifically, if a function
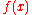 yields any of
yields any of  different outputs with equal probability and
different outputs with equal probability and  is sufficiently large, then we expect to obtain a pair of different arguments
is sufficiently large, then we expect to obtain a pair of different arguments 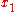 and
and 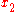 with
with 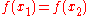 after evaluating the function for about
after evaluating the function for about 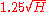 different arguments on average.
different arguments on average.
We consider the following experiment. From a set of H values we choose n values uniformly at random thereby allowing repetitions. Let p(n; H) be the probability that during this experiment at least one value is chosen more than once. This probability can be approximated as
Let n(p; H) be the smallest number of values we have to choose, such that the probability for finding a collision is at least p. By inverting this expression above, we find the following approximation
and assigning a 0.5 probability of collision we arrive at
Let Q(H) be the expected number of values we have to choose before finding the first collision. This number can be approximated by
As an example, if a 64-bit hash is used, there are approximately 1.8 × 1019 different outputs. If these are all equally probable (the best case), then it would take 'only' approximately 5.1 × 109 attempts to generate a collision using brute force. This value is called birthday bound and for n-bit codes it could be computed as 2n/2. Other examples are as follows:
It is easy to see that if the outputs of the function are distributed unevenly, then a collision can be found even faster. The notion of 'balance' of a hash function quantifies the resistance of the function to birthday attacks and allows the vulnerability of popular hashes such as MD and SHA to be estimated (Bellare and Kohno, 2004).
s can be susceptible to a birthday attack. A message is typically signed by first computing
is typically signed by first computing 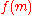 , where
, where  is a cryptographic hash function
is a cryptographic hash function
, and then using some secret key to sign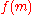 . Suppose Alice wants to trick Bob
. Suppose Alice wants to trick Bob
into signing a fraudulent contract. Alice prepares a fair contract and a fraudulent one
and a fraudulent one  . She then finds a number of positions where
. She then finds a number of positions where  can be changed without changing the meaning, such as inserting commas, empty lines, one versus two spaces after a sentence, replacing synonyms, etc. By combining these changes, she can create a huge number of variations on
can be changed without changing the meaning, such as inserting commas, empty lines, one versus two spaces after a sentence, replacing synonyms, etc. By combining these changes, she can create a huge number of variations on  which are all fair contracts.
which are all fair contracts.
In a similar manner, Alice also creates a huge number of variations on the fraudulent contract . She then applies the hash function to all these variations until she finds a version of the fair contract and a version of the fraudulent contract which have the same hash value,
. She then applies the hash function to all these variations until she finds a version of the fair contract and a version of the fraudulent contract which have the same hash value, 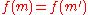 . She presents the fair version to Bob for signing. After Bob has signed, Alice takes the signature and attaches it to the fraudulent contract. This signature then "proves" that Bob signed the fraudulent contract.
. She presents the fair version to Bob for signing. After Bob has signed, Alice takes the signature and attaches it to the fraudulent contract. This signature then "proves" that Bob signed the fraudulent contract.
The probabilities differ slightly from the original birthday problem, as Alice gains nothing by finding two fair or two fraudulent contracts with the same hash. Alice's strategy is to generate pairs of one fair and one fraudulent contract. The birthday problem equations apply where is the number of pairs. The number of hashes Alice actually generates is
is the number of pairs. The number of hashes Alice actually generates is  .
.
To avoid this attack, the output length of the hash function used for a signature scheme can be chosen large enough so that the birthday attack becomes computationally infeasible, i.e. about twice as many bits as are needed to prevent an ordinary brute-force attack.
Pollard's rho algorithm for logarithms
is an example for an algorithm using a birthday attack for the computation of discrete logarithm
s.
Birthday attacks are often discussed as a potential weakness of the Internet's domain name service
system.
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
attack
Cryptanalysis
Cryptanalysis is the study of methods for obtaining the meaning of encrypted information, without access to the secret information that is normally required to do so. Typically, this involves knowing how the system works and finding a secret key...
that exploits the mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
behind the birthday problem in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. This attack can be used to abuse communication between two or more parties. The attack depends on the higher likelihood of collisions found between random attack attempts and a fixed degree of permutations (pigeonholes), as described in the birthday problem/paradox.
Understanding the problem
As an example, consider the scenario in which a teacher with a class of about 30 students asks for everybody's birthday, to determine whether any two students have the same birthday (corresponding to a hash collision as described below; for simplicity, ignore February 29). Intuitively, this chance may seem small. If the teacher picked a specific day (say September 16), then the chance that at least one student was born on that specific day is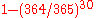 , about 7.9%. However, the probability that at least one student has the same birthday as any other student is nearly 70% (there are
, about 7.9%. However, the probability that at least one student has the same birthday as any other student is nearly 70% (there are 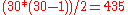 pairs of students that might match).
pairs of students that might match).The mathematics
Given a function , the goal of the attack is to find two different inputs
, the goal of the attack is to find two different inputs 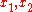 such that
such that 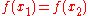 . Such a pair
. Such a pair  is called a collision. The method used to find a collision is simply to evaluate the function
is called a collision. The method used to find a collision is simply to evaluate the function  for different input values that may be chosen randomly or pseudorandomly until the same result is found more than once. Because of the birthday problem, this method can be rather efficient. Specifically, if a function
for different input values that may be chosen randomly or pseudorandomly until the same result is found more than once. Because of the birthday problem, this method can be rather efficient. Specifically, if a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
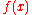 yields any of
yields any of  different outputs with equal probability and
different outputs with equal probability and  is sufficiently large, then we expect to obtain a pair of different arguments
is sufficiently large, then we expect to obtain a pair of different arguments 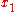 and
and 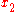 with
with 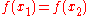 after evaluating the function for about
after evaluating the function for about 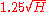 different arguments on average.
different arguments on average.We consider the following experiment. From a set of H values we choose n values uniformly at random thereby allowing repetitions. Let p(n; H) be the probability that during this experiment at least one value is chosen more than once. This probability can be approximated as
Let n(p; H) be the smallest number of values we have to choose, such that the probability for finding a collision is at least p. By inverting this expression above, we find the following approximation
and assigning a 0.5 probability of collision we arrive at
Let Q(H) be the expected number of values we have to choose before finding the first collision. This number can be approximated by
As an example, if a 64-bit hash is used, there are approximately 1.8 × 1019 different outputs. If these are all equally probable (the best case), then it would take 'only' approximately 5.1 × 109 attempts to generate a collision using brute force. This value is called birthday bound and for n-bit codes it could be computed as 2n/2. Other examples are as follows:
| Bits | Possible outputs (rounded)(H) |
Desired probability of random collision (rounded) (p) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10−18 | 10−15 | 10−12 | 10−9 | 10−6 | 0.1% | 1% | 25% | 50% | 75% | ||
| 16 | 6.6 × 104 | 2 | 2 | 2 | 2 | 2 | 11 | 36 | 1.9 × 102 | 3.0 × 102 | 4.3 × 102 |
| 32 | 4.3 × 109 | 2 | 2 | 2 | 2.9 | 93 | 2.9 × 103 | 9.3 × 103 | 5.0 × 104 | 7.7 × 104 | 1.1 × 105 |
| 64 | 1.8 × 1019 | 6.1 | 1.9 × 102 | 6.1 × 103 | 1.9 × 105 | 6.1 × 106 | 1.9 × 108 | 6.1 × 108 | 3.3 × 109 | 5.1 × 109 | 7.2 × 109 |
| 128 | 3.4 × 1038 | 2.6 × 1010 | 8.2 × 1011 | 2.6 × 1013 | 8.2 × 1014 | 2.6 × 1016 | 8.3 × 1017 | 2.6 × 1018 | 1.4 × 1019 | 2.2 × 1019 | 3.1 × 1019 |
| 256 | 1.2 × 1077 | 4.8 × 1029 | 1.5 × 1031 | 4.8 × 1032 | 1.5 × 1034 | 4.8 × 1035 | 1.5 × 1037 | 4.8 × 1037 | 2.6 × 1038 | 4.0 × 1038 | 5.7 × 1038 |
| 384 | 3.9 × 10115 | 8.9 × 1048 | 2.8 × 1050 | 8.9 × 1051 | 2.8 × 1053 | 8.9 × 1054 | 2.8 × 1056 | 8.9 × 1056 | 4.8 × 1057 | 7.4 × 1057 | 1.0 × 1058 |
| 512 | 1.3 × 10154 | 1.6 × 1068 | 5.2 × 1069 | 1.6 × 1071 | 5.2 × 1072 | 1.6 × 1074 | 5.2 × 1075 | 1.6 × 1076 | 8.8 × 1076 | 1.4 × 1077 | 1.9 × 1077 |
- Table shows number of hashes n(p) needed to achieve the given probability of success, assuming all hashes are equally likely. For comparison, 10−18 to 10−15 is the uncorrectable bit error rate of a typical hard disk http://arxiv.org/abs/cs/0701166. In theory, MD5MD5The MD5 Message-Digest Algorithm is a widely used cryptographic hash function that produces a 128-bit hash value. Specified in RFC 1321, MD5 has been employed in a wide variety of security applications, and is also commonly used to check data integrity...
, 128 bits, should stay within that range until about 820 billion documents, even if its possible outputs are many more.
It is easy to see that if the outputs of the function are distributed unevenly, then a collision can be found even faster. The notion of 'balance' of a hash function quantifies the resistance of the function to birthday attacks and allows the vulnerability of popular hashes such as MD and SHA to be estimated (Bellare and Kohno, 2004).
Digital signature susceptibility
Digital signatureDigital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
s can be susceptible to a birthday attack. A message
 is typically signed by first computing
is typically signed by first computing 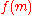 , where
, where  is a cryptographic hash function
is a cryptographic hash functionCryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
, and then using some secret key to sign
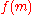 . Suppose Alice wants to trick Bob
. Suppose Alice wants to trick BobAlice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
into signing a fraudulent contract. Alice prepares a fair contract
 and a fraudulent one
and a fraudulent one  . She then finds a number of positions where
. She then finds a number of positions where  can be changed without changing the meaning, such as inserting commas, empty lines, one versus two spaces after a sentence, replacing synonyms, etc. By combining these changes, she can create a huge number of variations on
can be changed without changing the meaning, such as inserting commas, empty lines, one versus two spaces after a sentence, replacing synonyms, etc. By combining these changes, she can create a huge number of variations on  which are all fair contracts.
which are all fair contracts.In a similar manner, Alice also creates a huge number of variations on the fraudulent contract
 . She then applies the hash function to all these variations until she finds a version of the fair contract and a version of the fraudulent contract which have the same hash value,
. She then applies the hash function to all these variations until she finds a version of the fair contract and a version of the fraudulent contract which have the same hash value, 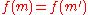 . She presents the fair version to Bob for signing. After Bob has signed, Alice takes the signature and attaches it to the fraudulent contract. This signature then "proves" that Bob signed the fraudulent contract.
. She presents the fair version to Bob for signing. After Bob has signed, Alice takes the signature and attaches it to the fraudulent contract. This signature then "proves" that Bob signed the fraudulent contract.The probabilities differ slightly from the original birthday problem, as Alice gains nothing by finding two fair or two fraudulent contracts with the same hash. Alice's strategy is to generate pairs of one fair and one fraudulent contract. The birthday problem equations apply where
 is the number of pairs. The number of hashes Alice actually generates is
is the number of pairs. The number of hashes Alice actually generates is  .
.To avoid this attack, the output length of the hash function used for a signature scheme can be chosen large enough so that the birthday attack becomes computationally infeasible, i.e. about twice as many bits as are needed to prevent an ordinary brute-force attack.
Pollard's rho algorithm for logarithms
Pollard's rho algorithm for logarithms
Pollard's rho algorithm for logarithms is an algorithm for solving the discrete logarithm problem analogous to Pollard's rho algorithm for solving the Integer factorization problem....
is an example for an algorithm using a birthday attack for the computation of discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
s.
Birthday attacks are often discussed as a potential weakness of the Internet's domain name service
Name server
In computing, a name server is a program or computer server that implements a name-service protocol. It maps a human-recognizable identifier to a system-internal, often numeric, identification or addressing component....
system.
External links
- "What is a digital signature and what is authentication?" from RSA Security's crypto FAQFAQFrequently asked questions are listed questions and answers, all supposed to be commonly asked in some context, and pertaining to a particular topic. "FAQ" is usually pronounced as an initialism rather than an acronym, but an acronym form does exist. Since the acronym FAQ originated in textual...
. - "Parallel collision search with cryptanalytic applications, by Michael Wiener and Paul C. van Oorschot
- "Birthday Attack" X5 Networks Crypto FAQs