Axiom schema of replacement
Encyclopedia
In set theory
, the axiom schema of replacement is a schema of axiom
s in Zermelo–Fraenkel set theory
(ZFC) that asserts that the image
of any set under any definable mapping
is also a set. It is necessary for the construction of certain infinite sets in ZFC.
The axiom schema is motivated by the idea that whether a class
is a set depends only on the cardinality of the class, not on the rank of its elements. Thus, if one class is "small enough" to be a set, and there is a bijection
from that class to a second class, the axiom states that the second class is also a set. However, because ZFC only speaks of sets, not proper classes, the schema is stated only for definable bijections, which are identified with their defining formulas.
(which may be a proper class) such that for every set x there is a unique set y such that P(x,y) holds. There is a corresponding definable function FP, where FP(X) = Y if and only if
P(X,Y); F will also be a proper class if P is. Consider the (possibly proper) class B defined such for every set y, y is in B if and only if there is an x in A with FP(x) = y. B is called the image of A under FP, and denoted FP(A) or (using set-builder notation
) {FP(x) : x ∈ A}.
The axiom schema of replacement states that if F is a definable class function, as above, and A is any set, then the image F(A) is also a set. This can be seen as a principle of smallness: the axiom states that if A is small enough to be a set, then F(A) is also small enough to be a set. It is implied by the stronger axiom of limitation of size
.
Because it is impossible to quantify over definable functions in first-order logic, one instance of the schema is included for each formula φ in the language of set theory with free variables among w1, ..., wn, A, x, y; but B is not free in φ. In the formal language of set theory, the axiom schema is: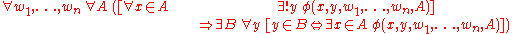
of the image is a set. In other words, the resulting set, B, is not required to be minimal.
This version of collection also lacks the uniqueness requirement on φ. Suppose that the free variables of φ are among w1, ..., wn, x, y; but neither A nor B is free in φ. Then the axiom schema is:
That is, the relation defined by φ is not required to be a function — some x in A may correspond to multiple y in B. In this case, the image set B whose existence is asserted must contain at least one such y for each x of the original set, with no guarantee that it will contain only one.
The axiom schema is sometimes stated without any restrictions on the predicate, φ: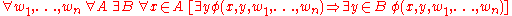
In this case, there may be elements x in A that are not associated to any other sets by φ. However, the axiom schema as stated requires that, if an element x of A is associated with at least one set y, then the image set B will contain at least one such y. The resulting axiom schema is also called the axiom schema of boundedness.
The axiom schema of collection is equivalent to the axiom schema of replacement over the remainder of the ZF axioms.
ω·2 = ω + ω (using the modern definition due to von Neumann) is the first ordinal that cannot be constructed without replacement. The axiom of infinity
asserts the existence of the infinite sequence ω = {0, 1,2,...}, and only this sequence. One would like to define ω·2 to be the union of the sequence {ω, ω + 1, ω + 2,...}. However, arbitrary class
es of ordinals need not be sets (the class of all ordinals is not a set, for example). Replacement allows one to replace each finite number n in ω with the corresponding ω + n, and guarantees that this class is a set. Note that one can easily construct a well-ordered set that is isomorphic to ω·2 without resorting to replacement – simply take the disjoint union
of two copies of ω, with the second copy greater than the first – but that this is not an ordinal since it is not totally ordered by inclusion.
Clearly then, the existence of an assignment of an ordinal to every well-ordered set requires replacement as well. Similarly the von Neumann cardinal assignment
which assigns a cardinal number
to each set requires replacement, as well as axiom of choice.
Every countable limit ordinal requires replacement for its construction analogously to ω·2. Larger ordinals rely on replacement less directly. For example ω1, the first uncountable ordinal
, can be constructed as follows – the set of countable well orders exists as a subset of P(N×N) by separation and powerset
(a relation
on A is a subset of A×A, and so an element of the power set P(A×A). A set of relations is thus a subset of P(A×A)). Replace each well-ordered set with its ordinal. This is the set of countable ordinals ω1, which can itself be shown to be uncountable. The construction uses replacement twice; once to ensure an ordinal assignment for each well ordered set and again to replace well ordered sets by their ordinals. This is a special case of the result of Hartogs number
, and the general case can be proved similarly.
The axiom of choice without replacement (ZC set theory) is not strong enough to show that Borel set
s are determined
; for this, replacement is required.
's 1908 axiomatisation of set theory (Z); its introduction by Adolf Fraenkel in 1922 is what makes modern set theory Zermelo-Fraenkel set theory (ZF). The axiom was independently invented by Thoralf Skolem
later in the same year. Although it is Skolem's final version of the axiom list that we use today, he usually gets no credit since each individual axiom was developed earlier by either Zermelo or Fraenkel.
The axiom schema of replacement drastically increases the strength of ZF, both in terms of the theorems it can prove and in terms of its proof-theoretic consistency strength, compared to Z. In particular, ZF proves the consistency
of Z, as the set Vω·2 is a model of Z constructible in ZF. (Gödel's second incompleteness theorem shows that each of these theories contains a sentence, "expressing" the theory's own consistency, that is unprovable in that theory, if that theory is consistent (this result is often loosely expressed as the claim that neither of these theories can prove its own consistency, if it is consistent, but the work of Solomon Feferman [1960] shows that care must be taken in stating the content of the second incompleteness theorem.) The cardinal number
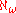is the first one which can be shown to exist in ZF but not in Z.
The axiom schema of replacement is not necessary for the proofs of most theorems of ordinary mathematics. Indeed, Zermelo set theory already can interpret second-order arithmetic
and much of type theory
in finite types, which in turn are sufficient to formalize the bulk of mathematics. A notable mathematical theorem that requires the axiom of replacement to be proved in ZF is the Borel determinacy theorem
.
The axiom of replacement does have an important role in the study of set theory itself. For example, the replacement schema is needed to construct the von Neumann ordinals from ω·2 onwards; without replacement, it would be necessary to find some other representation for ordinal number
s.
Although the axiom schema of replacement is a standard axiom in set theory today, it is often omitted from systems of type theory
and foundation systems in topos
theory.
, the other axiom schema in ZFC, is implied by the axiom schema of replacement and the axiom of empty set
. Recall that the axiom schema of specification includes
for each formula θ in the language of set theory in which B is not free.
The proof is as follows. Begin with a formula θ(C) that does not mention B, and a set A. If no element E of A satisfies θ then the set B desired by the relevant instance of the axiom schema of separation is the empty set. Otherwise, choose a fixed E in A such that θ(E) holds. Define a class function F such that F(D) = D if θ(D) holds and F(D) = E if θ(D) is false. Then the set B = F "A = A∩{x|θ(x)} exists, by the axiom of replacement, and is precisely the set B required for the axiom of specification.
This result shows that it is possible to axiomatize ZFC with a single infinite axiom schema. Because at least one such infinite schema is required (ZFC is not finitely axiomatizable), this shows that the axiom schema of replacement can stand as the only infinite axiom schema in ZFC if desired. Because the axiom schema of specification is not independent, it is sometimes omitted from contemporary statements of the Zermelo-Fraenkel axioms.
Specification is still important, however, for use in fragments of ZFC, because of historical considerations, and for comparison with alternative axiomatizations of set theory. A formulation of set theory that does not include the axiom of replacement will likely include some form of the axiom of specification, to ensure that its models contain a robust collection of sets. In the study of models of set theory, it is sometimes useful to consider models of ZFC without replacement.
The proof above uses the law of excluded middle
in assuming that if A is nonempty then it must contain an element (in intuitionistic logic, a set is "empty" if it does not contain an element, and "nonempty" is the formal negation of this, which is weaker than "does contain an element"). The axiom of specification is included in intuitionistic set theory
.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, the axiom schema of replacement is a schema of axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s in Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
(ZFC) that asserts that the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of any set under any definable mapping
Functional predicate
In formal logic and related branches of mathematics, a functional predicate, or function symbol, is a logical symbol that may be applied to an object term to produce another object term....
is also a set. It is necessary for the construction of certain infinite sets in ZFC.
The axiom schema is motivated by the idea that whether a class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
is a set depends only on the cardinality of the class, not on the rank of its elements. Thus, if one class is "small enough" to be a set, and there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
from that class to a second class, the axiom states that the second class is also a set. However, because ZFC only speaks of sets, not proper classes, the schema is stated only for definable bijections, which are identified with their defining formulas.
Statement
Suppose P is a definable binary relationRelation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
(which may be a proper class) such that for every set x there is a unique set y such that P(x,y) holds. There is a corresponding definable function FP, where FP(X) = Y if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
P(X,Y); F will also be a proper class if P is. Consider the (possibly proper) class B defined such for every set y, y is in B if and only if there is an x in A with FP(x) = y. B is called the image of A under FP, and denoted FP(A) or (using set-builder notation
Set-builder notation
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...
) {FP(x) : x ∈ A}.
The axiom schema of replacement states that if F is a definable class function, as above, and A is any set, then the image F(A) is also a set. This can be seen as a principle of smallness: the axiom states that if A is small enough to be a set, then F(A) is also small enough to be a set. It is implied by the stronger axiom of limitation of size
Axiom of limitation of size
In class theories, the axiom of limitation of size says that for any class C, C is a proper class, that is a class which is not a set , if and only if it can be mapped onto the class V of all sets....
.
Because it is impossible to quantify over definable functions in first-order logic, one instance of the schema is included for each formula φ in the language of set theory with free variables among w1, ..., wn, A, x, y; but B is not free in φ. In the formal language of set theory, the axiom schema is:
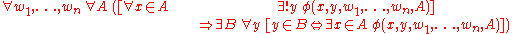
Axiom schema of collection
The axiom schema of collection is closely related to and frequently confused with the axiom schema of replacement. While replacement says that the image itself is a set, collection merely says that a superclassSuperSet
SuperSet Software was a group founded by friends and former Eyring Research Institute co-workers Drew Major, Dale Neibaur, Kyle Powell and later joined by Mark Hurst...
of the image is a set. In other words, the resulting set, B, is not required to be minimal.
This version of collection also lacks the uniqueness requirement on φ. Suppose that the free variables of φ are among w1, ..., wn, x, y; but neither A nor B is free in φ. Then the axiom schema is:
That is, the relation defined by φ is not required to be a function — some x in A may correspond to multiple y in B. In this case, the image set B whose existence is asserted must contain at least one such y for each x of the original set, with no guarantee that it will contain only one.
The axiom schema is sometimes stated without any restrictions on the predicate, φ:
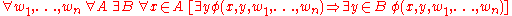
In this case, there may be elements x in A that are not associated to any other sets by φ. However, the axiom schema as stated requires that, if an element x of A is associated with at least one set y, then the image set B will contain at least one such y. The resulting axiom schema is also called the axiom schema of boundedness.
The axiom schema of collection is equivalent to the axiom schema of replacement over the remainder of the ZF axioms.
Example applications
The ordinal numberOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
ω·2 = ω + ω (using the modern definition due to von Neumann) is the first ordinal that cannot be constructed without replacement. The axiom of infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
asserts the existence of the infinite sequence ω = {0, 1,2,...}, and only this sequence. One would like to define ω·2 to be the union of the sequence {ω, ω + 1, ω + 2,...}. However, arbitrary class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
es of ordinals need not be sets (the class of all ordinals is not a set, for example). Replacement allows one to replace each finite number n in ω with the corresponding ω + n, and guarantees that this class is a set. Note that one can easily construct a well-ordered set that is isomorphic to ω·2 without resorting to replacement – simply take the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of two copies of ω, with the second copy greater than the first – but that this is not an ordinal since it is not totally ordered by inclusion.
Clearly then, the existence of an assignment of an ordinal to every well-ordered set requires replacement as well. Similarly the von Neumann cardinal assignment
Von Neumann cardinal assignment
The von Neumann cardinal assignment is a cardinal assignment which uses ordinal numbers. For a well-ordered set U, we define its cardinal number to be the smallest ordinal number equinumerous to U. More precisely:...
which assigns a cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
to each set requires replacement, as well as axiom of choice.
Every countable limit ordinal requires replacement for its construction analogously to ω·2. Larger ordinals rely on replacement less directly. For example ω1, the first uncountable ordinal
First uncountable ordinal
In mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
, can be constructed as follows – the set of countable well orders exists as a subset of P(N×N) by separation and powerset
Axiom of power set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
(a relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
on A is a subset of A×A, and so an element of the power set P(A×A). A set of relations is thus a subset of P(A×A)). Replace each well-ordered set with its ordinal. This is the set of countable ordinals ω1, which can itself be shown to be uncountable. The construction uses replacement twice; once to ensure an ordinal assignment for each well ordered set and again to replace well ordered sets by their ordinals. This is a special case of the result of Hartogs number
Hartogs number
In mathematics, specifically in axiomatic set theory, a Hartogs number is a particular kind of cardinal number. It was shown by Friedrich Hartogs in 1915, from ZF alone , that there is a least well-ordered cardinal greater than a given well-ordered cardinal.To define the Hartogs number of a set it...
, and the general case can be proved similarly.
The axiom of choice without replacement (ZC set theory) is not strong enough to show that Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s are determined
Determinacy
In set theory, a branch of mathematics, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.-Games:...
; for this, replacement is required.
History and philosophy
The axiom schema of replacement was not part of Ernst ZermeloErnst Zermelo
Ernst Friedrich Ferdinand Zermelo was a German mathematician, whose work has major implications for the foundations of mathematics and hence on philosophy. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem.-Life:He graduated...
's 1908 axiomatisation of set theory (Z); its introduction by Adolf Fraenkel in 1922 is what makes modern set theory Zermelo-Fraenkel set theory (ZF). The axiom was independently invented by Thoralf Skolem
Thoralf Skolem
Thoralf Albert Skolem was a Norwegian mathematician known mainly for his work on mathematical logic and set theory.-Life:...
later in the same year. Although it is Skolem's final version of the axiom list that we use today, he usually gets no credit since each individual axiom was developed earlier by either Zermelo or Fraenkel.
The axiom schema of replacement drastically increases the strength of ZF, both in terms of the theorems it can prove and in terms of its proof-theoretic consistency strength, compared to Z. In particular, ZF proves the consistency
Consistency
Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...
of Z, as the set Vω·2 is a model of Z constructible in ZF. (Gödel's second incompleteness theorem shows that each of these theories contains a sentence, "expressing" the theory's own consistency, that is unprovable in that theory, if that theory is consistent (this result is often loosely expressed as the claim that neither of these theories can prove its own consistency, if it is consistent, but the work of Solomon Feferman [1960] shows that care must be taken in stating the content of the second incompleteness theorem.) The cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
is the first one which can be shown to exist in ZF but not in Z.The axiom schema of replacement is not necessary for the proofs of most theorems of ordinary mathematics. Indeed, Zermelo set theory already can interpret second-order arithmetic
Second-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
and much of type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
in finite types, which in turn are sufficient to formalize the bulk of mathematics. A notable mathematical theorem that requires the axiom of replacement to be proved in ZF is the Borel determinacy theorem
Borel determinacy theorem
In descriptive set theory, the Borel determinacy theorem states that any Gale-Stewart game whose winning set is a Borel set is determined, meaning that one of the two players will have a winning strategy for the game. It was proved by Donald A. Martin in 1975...
.
The axiom of replacement does have an important role in the study of set theory itself. For example, the replacement schema is needed to construct the von Neumann ordinals from ω·2 onwards; without replacement, it would be necessary to find some other representation for ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s.
Although the axiom schema of replacement is a standard axiom in set theory today, it is often omitted from systems of type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
and foundation systems in topos
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
theory.
Relation to the axiom schema of specification
The axiom schema of specificationAxiom schema of specification
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axioms in Zermelo-Fraenkel set theory...
, the other axiom schema in ZFC, is implied by the axiom schema of replacement and the axiom of empty set
Axiom of empty set
In axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
. Recall that the axiom schema of specification includes
for each formula θ in the language of set theory in which B is not free.
The proof is as follows. Begin with a formula θ(C) that does not mention B, and a set A. If no element E of A satisfies θ then the set B desired by the relevant instance of the axiom schema of separation is the empty set. Otherwise, choose a fixed E in A such that θ(E) holds. Define a class function F such that F(D) = D if θ(D) holds and F(D) = E if θ(D) is false. Then the set B = F "A = A∩{x|θ(x)} exists, by the axiom of replacement, and is precisely the set B required for the axiom of specification.
This result shows that it is possible to axiomatize ZFC with a single infinite axiom schema. Because at least one such infinite schema is required (ZFC is not finitely axiomatizable), this shows that the axiom schema of replacement can stand as the only infinite axiom schema in ZFC if desired. Because the axiom schema of specification is not independent, it is sometimes omitted from contemporary statements of the Zermelo-Fraenkel axioms.
Specification is still important, however, for use in fragments of ZFC, because of historical considerations, and for comparison with alternative axiomatizations of set theory. A formulation of set theory that does not include the axiom of replacement will likely include some form of the axiom of specification, to ensure that its models contain a robust collection of sets. In the study of models of set theory, it is sometimes useful to consider models of ZFC without replacement.
The proof above uses the law of excluded middle
Law of excluded middle
In logic, the law of excluded middle is the third of the so-called three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is....
in assuming that if A is nonempty then it must contain an element (in intuitionistic logic, a set is "empty" if it does not contain an element, and "nonempty" is the formal negation of this, which is weaker than "does contain an element"). The axiom of specification is included in intuitionistic set theory
Constructive set theory
Constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. That is, it uses the usual first-order language of classical set theory, and although of course the logic is constructive, there is no explicit use of constructive types...
.