Axiom of power set
Encyclopedia
In mathematics
, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.
In the formal language
of the Zermelo–Fraenkel axioms, the axiom reads:
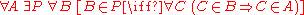
where P stands for the power set of A,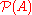
. In English, this says:
By the axiom of extensionality
this set is unique.
We call the set
the power set of A. Thus, the essence of the axiom is that every set has a power set.
The axiom of power set appears in most axiomatizations of set theory. It is generally considered uncontroversial, although constructive set theory
prefers a weaker version to resolve concerns about predicativity.
of two sets
and 
:
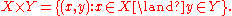
Notice that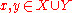
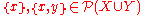
and thus the Cartesian product is a set since
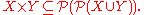
One may define the Cartesian product of any finite collection
of sets recursively:
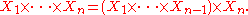
Note that the existence of the Cartesian product can be proved without using the power set axiom, as in the case of the Kripke–Platek set theory
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.
In the formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
of the Zermelo–Fraenkel axioms, the axiom reads:
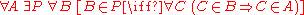
where P stands for the power set of A,
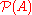. In English, this says:- Given any set A, there isExistential quantificationIn predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
a set
such that, given any set B, B is a member of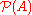 
if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
B is a subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of A. (Subset is not used in the formal definition above because the axiom of power set is an axiom that may need to be stated without reference to the concept of subset.)
By the axiom of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
this set is unique.
We call the set
the power set of A. Thus, the essence of the axiom is that every set has a power set.The axiom of power set appears in most axiomatizations of set theory. It is generally considered uncontroversial, although constructive set theory
Constructive set theory
Constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. That is, it uses the usual first-order language of classical set theory, and although of course the logic is constructive, there is no explicit use of constructive types...
prefers a weaker version to resolve concerns about predicativity.
Consequences
The Power Set Axiom allows a simple definition of the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of two sets
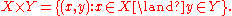
and :Notice that
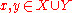
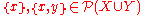
and thus the Cartesian product is a set since
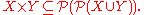
One may define the Cartesian product of any finite collection
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of sets recursively:
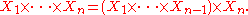
Note that the existence of the Cartesian product can be proved without using the power set axiom, as in the case of the Kripke–Platek set theory
Kripke–Platek set theory
The Kripke–Platek axioms of set theory are a system of axioms for axiomatic set theory developed by Saul Kripke and Richard Platek. The axiom system, written in first-order logic, has an infinite number of axioms because an infinite axiom schema is used.KP is weaker than Zermelo–Fraenkel set theory...
.