
Axiom of infinity
Encyclopedia
In axiomatic set theory and the branches of logic
, mathematics
, and computer science
that use it, the axiom of infinity is one of the axiom
s of Zermelo-Fraenkel set theory. It guarantees the existence of at least one infinite set, namely a set containing the natural number
s.
of the Zermelo-Fraenkel axioms, the axiom reads:
In words, there is
a set I (the set which is postulated to be infinite), such that the empty set
is in I and such that whenever any x is a member of I, the set formed by taking the union
of x with its singleton {x} is also a member of I. Such a set is sometimes called an inductive set
.
s. In this encoding, zero is the empty set:
The number 1 is the successor of 0:
Likewise, 2 is the successor of 1:
and so on. A consequence of this definition is that every natural number is equal to the set of all preceding natural numbers.
This construction forms the natural numbers. However, the other axioms are insufficient to prove the existence of the set of all natural numbers. Therefore its existence is taken as an axiom—the axiom of infinity. This axiom asserts that there is a set I that contains 0 and is closed
under the operation of taking the successor; that is, for each element of I, the successor of that element is also in I.
Thus the essence of the axiom is:
The axiom of infinity is also one of the von Neumann-Bernays-Gödel axioms.
can be applied to remove unwanted elements, leaving the set N of all natural numbers. This set is unique by the axiom of extensionality
.
To extract the natural numbers, we need a definition of which sets are natural numbers. The natural numbers can be defined in a way which does not assume any axioms except the axiom of extensionality
and the axiom of induction
—a natural number is either zero or a successor and each of its elements is either zero or a successor of another of its elements. In formal language, the definition says:
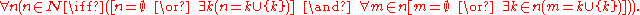
Or, even more formally:
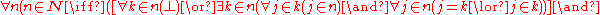
Here, denotes the logical constant "false", so
denotes the logical constant "false", so 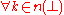 is a formula that holds only if n is the empty set.
is a formula that holds only if n is the empty set.
 be the formula that says `x is inductive'; i.e.
be the formula that says `x is inductive'; i.e. 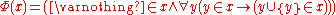 . Informally, what we will do is take the intersection of all inductive sets. More formally, we wish to prove the existence of a unique set
. Informally, what we will do is take the intersection of all inductive sets. More formally, we wish to prove the existence of a unique set  such that
such that
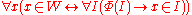 (*)
(*)
For existence, we will use the Axiom of Infinity combined with the Axiom schema of specification
. Let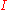 be an inductive set guaranteed by the Axiom of Infinity. Then we use the Axiom Schema of Specification to define our set
be an inductive set guaranteed by the Axiom of Infinity. Then we use the Axiom Schema of Specification to define our set 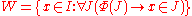 - i.e.
- i.e.  is the set of all elements of
is the set of all elements of 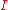 which happen also to be elements of every other inductive set. This clearly satisfies the hypothesis of (*), since if
which happen also to be elements of every other inductive set. This clearly satisfies the hypothesis of (*), since if 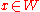 , then
, then  is in every inductive set, and if
is in every inductive set, and if  is in every inductive set, it is in particular in
is in every inductive set, it is in particular in 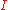 , so it must also be in
, so it must also be in  .
.
For uniqueness, first note that any set which satisfies (*) is itself inductive, since 0 is in all inductive sets, and if an element is in all inductive sets, then by the inductive property so is its successor. Thus if there were another set
is in all inductive sets, then by the inductive property so is its successor. Thus if there were another set 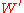 which satisfied (*) we would have that
which satisfied (*) we would have that 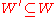 since
since  is inductive, and
is inductive, and 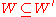 since
since  is inductive. Thus
is inductive. Thus  . Let
. Let  denote this unique element.
denote this unique element.
This definition is convenient because the principle of induction
immediately follows: If is inductive, then also
is inductive, then also  , so that
, so that  .
.
Both these methods produce systems which satisfy the axioms of second-order arithmetic
, since the axiom of power set
allows us to quantify over the power set of , as in second-order logic
, as in second-order logic
. Thus they both completely determine isomorphic
systems, and since they are isomorphic under the identity map
, they must in fact be equal.
Indeed, using the Von Neumann universe
, we can make a model of the axioms where the axiom of infinity is replaced by its negation. It is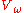 , the class of hereditarily finite set
, the class of hereditarily finite set
s, with the inherited element relation.
The cardinality of the set of natural numbers, aleph null (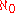 ), has many of the properties of a large cardinal. Thus the axiom of infinity is sometimes regarded as the first large cardinal axiom, and conversely large cardinal axioms are sometimes called stronger axioms of infinity.
), has many of the properties of a large cardinal. Thus the axiom of infinity is sometimes regarded as the first large cardinal axiom, and conversely large cardinal axioms are sometimes called stronger axioms of infinity.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
that use it, the axiom of infinity is one of the axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s of Zermelo-Fraenkel set theory. It guarantees the existence of at least one infinite set, namely a set containing the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s.
Formal statement
In the formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
of the Zermelo-Fraenkel axioms, the axiom reads:

In words, there is
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
a set I (the set which is postulated to be infinite), such that the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is in I and such that whenever any x is a member of I, the set formed by taking the union
Axiom of union
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
of x with its singleton {x} is also a member of I. Such a set is sometimes called an inductive set
Inductive set (axiom of infinity)
In the context of the axiom of infinity, an inductive set is a set X with the property that, for every x \in X, the successor x' of x is also an element of X and the set X contains the empty set \varnothing....
.
Interpretation and consequences
This axiom is closely related to the standard construction of the naturals in set theory, in which the successor of x is defined as x ∪ {x}. If x is a set, then it follows from the other axioms of set theory that this successor is also a uniquely defined set. Successors are used to define the usual set-theoretic encoding of the natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s. In this encoding, zero is the empty set:
- 0 = {}.
The number 1 is the successor of 0:
- 1 = 0 ∪ {0} = {} ∪ {0} = {0}.
Likewise, 2 is the successor of 1:
- 2 = 1 ∪ {1} = {0} ∪ {1} = {0,1},
and so on. A consequence of this definition is that every natural number is equal to the set of all preceding natural numbers.
This construction forms the natural numbers. However, the other axioms are insufficient to prove the existence of the set of all natural numbers. Therefore its existence is taken as an axiom—the axiom of infinity. This axiom asserts that there is a set I that contains 0 and is closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under the operation of taking the successor; that is, for each element of I, the successor of that element is also in I.
Thus the essence of the axiom is:
- There is a set, I, that includes all the natural numbers.
The axiom of infinity is also one of the von Neumann-Bernays-Gödel axioms.
Extracting the natural numbers from the infinite set
The infinite set I is a superset of the natural numbers. To show that the natural numbers themselves constitute a set, the axiom schema of specificationAxiom schema of specification
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axioms in Zermelo-Fraenkel set theory...
can be applied to remove unwanted elements, leaving the set N of all natural numbers. This set is unique by the axiom of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
.
To extract the natural numbers, we need a definition of which sets are natural numbers. The natural numbers can be defined in a way which does not assume any axioms except the axiom of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
and the axiom of induction
Epsilon-induction
In mathematics, \in-induction is a variant of transfinite induction, which can be used in set theory to prove that all sets satisfy a given property P[x]. If the truth of the property for x follows from its truth for all elements of x, for every set x, then the property is true of all sets...
—a natural number is either zero or a successor and each of its elements is either zero or a successor of another of its elements. In formal language, the definition says:
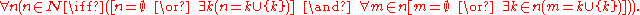
Or, even more formally:
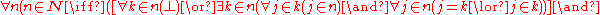
Here,
 denotes the logical constant "false", so
denotes the logical constant "false", so 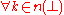 is a formula that holds only if n is the empty set.
is a formula that holds only if n is the empty set.Alternate
An alternate method is the following. Let be the formula that says `x is inductive'; i.e.
be the formula that says `x is inductive'; i.e. 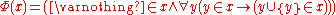 . Informally, what we will do is take the intersection of all inductive sets. More formally, we wish to prove the existence of a unique set
. Informally, what we will do is take the intersection of all inductive sets. More formally, we wish to prove the existence of a unique set  such that
such that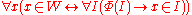 (*)
(*)For existence, we will use the Axiom of Infinity combined with the Axiom schema of specification
Axiom schema of specification
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axioms in Zermelo-Fraenkel set theory...
. Let
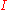 be an inductive set guaranteed by the Axiom of Infinity. Then we use the Axiom Schema of Specification to define our set
be an inductive set guaranteed by the Axiom of Infinity. Then we use the Axiom Schema of Specification to define our set 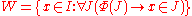 - i.e.
- i.e.  is the set of all elements of
is the set of all elements of 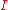 which happen also to be elements of every other inductive set. This clearly satisfies the hypothesis of (*), since if
which happen also to be elements of every other inductive set. This clearly satisfies the hypothesis of (*), since if 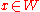 , then
, then  is in every inductive set, and if
is in every inductive set, and if  is in every inductive set, it is in particular in
is in every inductive set, it is in particular in 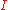 , so it must also be in
, so it must also be in  .
.For uniqueness, first note that any set which satisfies (*) is itself inductive, since 0 is in all inductive sets, and if an element
 is in all inductive sets, then by the inductive property so is its successor. Thus if there were another set
is in all inductive sets, then by the inductive property so is its successor. Thus if there were another set 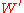 which satisfied (*) we would have that
which satisfied (*) we would have that 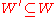 since
since  is inductive, and
is inductive, and 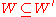 since
since  is inductive. Thus
is inductive. Thus  . Let
. Let  denote this unique element.
denote this unique element.This definition is convenient because the principle of induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
immediately follows: If
 is inductive, then also
is inductive, then also  , so that
, so that  .
.Both these methods produce systems which satisfy the axioms of second-order arithmetic
Second-order arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. It was introduced by David Hilbert and Paul Bernays in their...
, since the axiom of power set
Axiom of power set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
allows us to quantify over the power set of
 , as in second-order logic
, as in second-order logicSecond-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
. Thus they both completely determine isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
systems, and since they are isomorphic under the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
, they must in fact be equal.
Independence
The axiom of infinity cannot be derived from the rest of the axioms of ZFC, if these other axioms are consistent. Nor can it be refuted, if all of ZFC is consistent.Indeed, using the Von Neumann universe
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
, we can make a model of the axioms where the axiom of infinity is replaced by its negation. It is
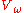 , the class of hereditarily finite set
, the class of hereditarily finite setHereditarily finite set
In mathematics and set theory, hereditarily finite sets are defined recursively as finite sets consisting of 0 or more hereditarily finite sets.-Formal definition:...
s, with the inherited element relation.
The cardinality of the set of natural numbers, aleph null (
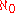 ), has many of the properties of a large cardinal. Thus the axiom of infinity is sometimes regarded as the first large cardinal axiom, and conversely large cardinal axioms are sometimes called stronger axioms of infinity.
), has many of the properties of a large cardinal. Thus the axiom of infinity is sometimes regarded as the first large cardinal axiom, and conversely large cardinal axioms are sometimes called stronger axioms of infinity.


