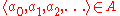Determinacy
Encyclopedia
In set theory
, a branch of mathematics
, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.
s.
In this sort of game we consider two players, often named I and II, who take turns playing natural numbers, with I going first. They play "forever"; that is, their plays are indexed by the natural numbers. When they're finished, a predetermined condition decides which player won. This condition need not be specified by any definable rule; it may simply be an arbitrary (infinitely long) lookup table
saying who has won given a particular sequence of plays.
More formally, consider a subset A of Baire space
; recall that the latter consists of all ω-sequences of natural numbers. Then in the game GA,
I plays a natural number a0, then II plays a1, then I plays a2, and so on. Then I wins the game if and only if
and otherwise II wins. A is then called the payoff set of GA.
It is assumed that each player can see all moves preceding each of his moves, and also knows the winning condition.
More formally, a strategy for player I (for a game in the sense of the preceding subsection) is a function that accepts as an argument any finite sequence of natural numbers, of even length, and returns a natural number. If σ is such a strategy and <a0,…,a2n-1>
is a sequence of plays, then σ(<a0,…,a2n-1>) is the next play I will make, if he is following the strategy σ. Strategies for II are just the same, substituting "odd" for "even".
Note that we have said nothing, as yet, about whether a strategy is in any way good. A strategy might direct a player to make aggressively bad moves, and it would still be a strategy. In fact it is not necessary even to know the winning condition for a game, to know what strategies exist for the game.
is an element of A.
Familiar real-world games of perfect information, such as chess
or tic-tac-toe
, are always finished in a finite number of moves. If such a game is modified so that a particular player wins under any condition where the game would have been called a draw, then it is always determined. The condition that the game is always over (i.e. all possible extensions of the finite position result in a win for the same player) in a finite number of moves corresponds to the topological condition that the set A giving the winning condition for GA is clopen
in the topology
of Baire space
.
For example, modifying the rules of chess to make drawn games a win for Black makes chess a determined game. As it happens, chess has a finite number of positions and a draw-by-repetition rules, so with these modified rules, if play continues long enough without White having won, then Black can eventually force a win (due to the modification of draw = win for black).
It is an instructive exercise to figure out how to represent such games as games in the context of this article.
The proof that such games are determined is rather simple: Player I simply plays not to lose; that is, he plays to make sure that player II does not have a winning strategy after Is move. If player I cannot do this, then it means player II had a winning strategy from the beginning. On the other hand, if player I can play in this way, then he must win, because the game will be over after some finite number of moves, and he can't have lost at that point.
This proof does not actually require that the game always be over in a finite number of moves, only that it be over in a finite number of moves whenever II wins. That condition, topologically, is that the set A is closed
. This fact--that all closed games are determined--is called the Gale-Stewart theorem. Note that by symmetry, all open games are determined as well. (A game is open if I can win only by winning in a finite number of moves.)
games was shown by Wolfe in 1955. Over the following 20 years, additional research using ever-more-complicated arguments established that third and fourth levels of the Borel hierarchy are determined.
In 1975, Donald A. Martin
proved that all Borel
games are determined; that is, if A is a Borel subset of Baire space, then GA is determined. This result, known as Borel determinacy, is the best possible determinacy result provable in ZFC, in the sense that the determinacy of the next higher Wadge class
is not provable in ZFC.
In 1971, before Martin obtained his proof, Harvey Friedman
showed that any proof of Borel determinacy must use the axiom of replacement in an essential way, in order to iterate the powerset axiom
transfinitely often. Friedman's work gives a level-by-level result detailing how many iterations of the powerset axiom are necessary to guarantee determinacy at each level of the Borel hierarchy
.
es, higher in the Wadge hierarchy
, and the determinacy of such pointclasses, in turn, proves the existence of inner model
s of slightly weaker large cardinal axioms than those used to prove the determinacy of the pointclass in the first place.
Measurable cardinal
It follows from the existence of a measurable cardinal that every analytic
game (also called a Σ11 game) is determined, or equivalently that every coanalytic (or Π11) game is determined. (See Projective hierarchy for definitions.)
Actually an apparently stronger result follows: If there is a measurable cardinal, then every game in the first ω2 levels of the difference hierarchy over Π11 is determined. This is only apparently stronger; ω2-Π11 determinacy turns out to be equivalent to Π11 determinacy.
From the existence of more measurable cardinals, one can prove the determinacy of more levels of the difference hierarchy over Π11.
Woodin cardinal
If there is a Woodin cardinal with a measurable cardinal above it, then Π12 determinacy holds. More generally, if there are n Woodin cardinals with a measurable cardinal above them all, then Π1n+1 determinacy holds. From Π1n+1 determinacy, it follows that there is a transitive
inner model
containing n Woodin cardinals.
Axiom of determinacy
The axiom of determinacy, or AD, asserts that every two-player game of perfect information of length ω, in which the players play naturals, is determined.
AD is provably false from ZFC; using the axiom of choice one may prove the existence of a non-determined game. However, if there are infinitely many Woodin cardinals with a measurable above them all, then L(R)
is a model of ZF that satisfies AD.
This does not quite imply that A has the property of Baire, but it comes close: A simple modification of the argument shows that if Γ is an adequate pointclass
such that every game in Γ is determined, then every set of reals in Γ has the property of Baire.
In fact this result is not optimal; by considering the unfolded Banach-Mazur game we can show that determinacy of Γ (for Γ with sufficient closure properties) implies that every set of reals that is the projection of a set in Γ has the property of Baire. So for example the existence of a measurable cardinal implies Π11 determinacy, which in turn implies that every Σ12 set of reals has the property of Baire.
By considering other games, we can show that Π1n determinacy implies that every Σ1n+1 set of reals has the property of Baire, is Lebesgue measurable (in fact universally measurable) and has the perfect set property
.
proved that the second-order theory
of n successors is decidable.
A key component of the proof requires showing determinacy of parity game
s, which lie in the third
level of the Borel hierarchy
.
, the Wadge game
G(A,B) is determined. Similarly for a pointclass
Γ, Γ Wadge determinacy is the statement that for all sets A,B in Γ, the Wadge game G(A,B) is determined.
Wadge determinacy implies the semilinear ordering principle
for the Wadge order
. Another consequence of Wadge determinacy is the perfect set property
.
In general, Γ Wadge determinacy is a consequence of the determinacy of Boolean combinations of sets in Γ. In the projective hierarchy, Π11 Wadge determinacy is equivalent to Π11 determinacy, as proved by Harrington. This result was extendend by Hjorth to prove that Π12 Wadge determinacy (and in fact the semilinear ordering principle for Π12) already implies Π12 determinacy.
distribution of outcomes to opposing mixed strategies can be calculated. A game that requires mixed strategies is defined as determined if a strategy exists that yields a minimum expected value
(over possible counter-strategies) that exceeds a given value. Against this definition, all finite two player zero-sum games are clearly determined. However, the determinacy of infinite games of imperfect information (Blackwell games) is less clear.
In 1969 David Blackwell
proved that some "infinite games with imperfect information" (now called "Blackwell games") are determined, and in 1998 Donald A. Martin
proved that ordinary (perfect-information game) determinacy for a boldface pointclass implies Blackwell determinacy for the pointclass. This, combined with the Borel determinacy theorem of Martin, implies that all Blackwell games with Borel payoff functions are determined.
Martin conjectured that ordinary determinacy and Blackwell determinacy for infinite games are equivalent in a strong sense (i.e. that Blackwell determinacy for a boldface pointclass in turn implies ordinary determinacy for that pointclass), but as of 2010, it has not been proven that Blackwell determinacy implies perfect-information-game determinacy.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.
Games
The first sort of game we shall consider is the two-player game of perfect information of length ω, in which the players play natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s.
In this sort of game we consider two players, often named I and II, who take turns playing natural numbers, with I going first. They play "forever"; that is, their plays are indexed by the natural numbers. When they're finished, a predetermined condition decides which player won. This condition need not be specified by any definable rule; it may simply be an arbitrary (infinitely long) lookup table
Lookup table
In computer science, a lookup table is a data structure, usually an array or associative array, often used to replace a runtime computation with a simpler array indexing operation. The savings in terms of processing time can be significant, since retrieving a value from memory is often faster than...
saying who has won given a particular sequence of plays.
More formally, consider a subset A of Baire space
Baire space (set theory)
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
; recall that the latter consists of all ω-sequences of natural numbers. Then in the game GA,
I plays a natural number a0, then II plays a1, then I plays a2, and so on. Then I wins the game if and only if
and otherwise II wins. A is then called the payoff set of GA.
It is assumed that each player can see all moves preceding each of his moves, and also knows the winning condition.
Strategies
Informally, a strategy for a player is a way of playing in which his plays are entirely determined by the foregoing plays. Again, such a "way" does not have to be capable of being captured by any explicable "rule", but may simply be a lookup table.More formally, a strategy for player I (for a game in the sense of the preceding subsection) is a function that accepts as an argument any finite sequence of natural numbers, of even length, and returns a natural number. If σ is such a strategy and <a0,…,a2n-1>
is a sequence of plays, then σ(<a0,…,a2n-1>) is the next play I will make, if he is following the strategy σ. Strategies for II are just the same, substituting "odd" for "even".
Note that we have said nothing, as yet, about whether a strategy is in any way good. A strategy might direct a player to make aggressively bad moves, and it would still be a strategy. In fact it is not necessary even to know the winning condition for a game, to know what strategies exist for the game.
Winning strategies
A strategy is winning if the player following it must necessarily win, no matter what his opponent plays. For example if σ is a strategy for I, then σ is a winning strategy for I in the game GA if, for any sequence of natural numbers to be played by II, say <a1,a3,a5,…>, the sequence of plays produced by σ when II plays thus, namelyis an element of A.
Determined games
A (class of) game(s) is determined if for all instance of the game there is a winning strategy for one of the players (not necessarily the same player for each instance). Note that there cannot be a winning strategy for both players for the same game, for if there were, the two strategies could be played against each other. The resulting outcome would then, by hypothesis, be a win for both players, which is impossible.Determinacy from elementary considerations
All finite games of perfect information in which draws do not occur are determined.Familiar real-world games of perfect information, such as chess
Chess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
or tic-tac-toe
Tic-tac-toe
Tic-tac-toe, also called wick wack woe and noughts and crosses , is a pencil-and-paper game for two players, X and O, who take turns marking the spaces in a 3×3 grid. The X player usually goes first...
, are always finished in a finite number of moves. If such a game is modified so that a particular player wins under any condition where the game would have been called a draw, then it is always determined. The condition that the game is always over (i.e. all possible extensions of the finite position result in a win for the same player) in a finite number of moves corresponds to the topological condition that the set A giving the winning condition for GA is clopen
Clopen set
In topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
in the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of Baire space
Baire space (set theory)
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
.
For example, modifying the rules of chess to make drawn games a win for Black makes chess a determined game. As it happens, chess has a finite number of positions and a draw-by-repetition rules, so with these modified rules, if play continues long enough without White having won, then Black can eventually force a win (due to the modification of draw = win for black).
It is an instructive exercise to figure out how to represent such games as games in the context of this article.
The proof that such games are determined is rather simple: Player I simply plays not to lose; that is, he plays to make sure that player II does not have a winning strategy after Is move. If player I cannot do this, then it means player II had a winning strategy from the beginning. On the other hand, if player I can play in this way, then he must win, because the game will be over after some finite number of moves, and he can't have lost at that point.
This proof does not actually require that the game always be over in a finite number of moves, only that it be over in a finite number of moves whenever II wins. That condition, topologically, is that the set A is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
. This fact--that all closed games are determined--is called the Gale-Stewart theorem. Note that by symmetry, all open games are determined as well. (A game is open if I can win only by winning in a finite number of moves.)
Determinacy from ZFC
Gale and Stewart proved the open and closed games are determined. Determinacy for second level of the Borel hierarchyBorel hierarchy
In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
games was shown by Wolfe in 1955. Over the following 20 years, additional research using ever-more-complicated arguments established that third and fourth levels of the Borel hierarchy are determined.
In 1975, Donald A. Martin
Donald A. Martin
Donald A. Martin is a set theorist and philosopher of mathematics at UCLA, where he is a member of the faculty of mathematics and philosophy....
proved that all Borel
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
games are determined; that is, if A is a Borel subset of Baire space, then GA is determined. This result, known as Borel determinacy, is the best possible determinacy result provable in ZFC, in the sense that the determinacy of the next higher Wadge class
Wadge hierarchy
In descriptive set theory, Wadge degrees are levels of complexity for sets of reals. Sets are compared by continuous reductions. The Wadge hierarchy is the structure of Wadge degrees.- Wadge degrees :...
is not provable in ZFC.
In 1971, before Martin obtained his proof, Harvey Friedman
Harvey Friedman
Harvey Friedman is a mathematical logician at Ohio State University in Columbus, Ohio. He is noted especially for his work on reverse mathematics, a project intended to derive the axioms of mathematics from the theorems considered to be necessary...
showed that any proof of Borel determinacy must use the axiom of replacement in an essential way, in order to iterate the powerset axiom
Axiom of power set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
transfinitely often. Friedman's work gives a level-by-level result detailing how many iterations of the powerset axiom are necessary to guarantee determinacy at each level of the Borel hierarchy
Borel hierarchy
In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
.
Determinacy and large cardinals
There is an intimate relationship between determinacy and large cardinals. In general, stronger large cardinal axioms prove the determinacy of larger pointclassPointclass
In the mathematical field of descriptive set theory, a pointclass is a collection of sets of points, where a point is ordinarily understood to be an element of some perfect Polish space. In practice, a pointclass is usually characterized by some sort of definability property; for example, the...
es, higher in the Wadge hierarchy
Wadge hierarchy
In descriptive set theory, Wadge degrees are levels of complexity for sets of reals. Sets are compared by continuous reductions. The Wadge hierarchy is the structure of Wadge degrees.- Wadge degrees :...
, and the determinacy of such pointclasses, in turn, proves the existence of inner model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
s of slightly weaker large cardinal axioms than those used to prove the determinacy of the pointclass in the first place.
Measurable cardinalMeasurable cardinal- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
s
It follows from the existence of a measurable cardinal that every analyticAnalytic set
In descriptive set theory, a subset of a Polish space X is an analytic set if it is a continuous image of a Polish space. These sets were first defined by and his student .- Definition :There are several equivalent definitions of analytic set...
game (also called a Σ11 game) is determined, or equivalently that every coanalytic (or Π11) game is determined. (See Projective hierarchy for definitions.)
Actually an apparently stronger result follows: If there is a measurable cardinal, then every game in the first ω2 levels of the difference hierarchy over Π11 is determined. This is only apparently stronger; ω2-Π11 determinacy turns out to be equivalent to Π11 determinacy.
From the existence of more measurable cardinals, one can prove the determinacy of more levels of the difference hierarchy over Π11.
Woodin cardinalWoodin cardinalIn set theory, a Woodin cardinal is a cardinal number λ such that for all functionsthere exists a cardinal κ In set theory, a Woodin cardinal is a cardinal number λ such that for all functions...
s
If there is a Woodin cardinal with a measurable cardinal above it, then Π12 determinacy holds. More generally, if there are n Woodin cardinals with a measurable cardinal above them all, then Π1n+1 determinacy holds. From Π1n+1 determinacy, it follows that there is a transitiveTransitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
inner model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
containing n Woodin cardinals.
Projective determinacy
If there are infinitely many Woodin cardinals, then projective determinacy holds; that is, every game whose winning condition is a projective set is determined. From projective determinacy it follows that, for every natural number n, there is a transitive inner model which satisfies that there are n Woodin cardinals.Axiom of determinacyAxiom of determinacyThe axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
The axiom of determinacy, or AD, asserts that every two-player game of perfect information of length ω, in which the players play naturals, is determined.AD is provably false from ZFC; using the axiom of choice one may prove the existence of a non-determined game. However, if there are infinitely many Woodin cardinals with a measurable above them all, then L(R)
L(R)
In set theory, L is the smallest transitive inner model of ZF containing all the ordinals and all the reals. It can be constructed in a manner analogous to the construction of L , by adding in all the reals at the start, and then iterating the definable powerset operation through all the...
is a model of ZF that satisfies AD.
Regularity properties for sets of reals
If A is a subset of Baire space such that the Banach-Mazur game for A is determined, then either II has a winning strategy, in which case A is meager, or I has a winning strategy, in which case A is comeager on some open neighborhood.This does not quite imply that A has the property of Baire, but it comes close: A simple modification of the argument shows that if Γ is an adequate pointclass
Adequate pointclass
In the mathematical field of descriptive set theory, a pointclass can be called adequate if it contains all recursive pointsets and is closed under recursive substitution, bounded universal and existential quantification and preimages by recursive functions....
such that every game in Γ is determined, then every set of reals in Γ has the property of Baire.
In fact this result is not optimal; by considering the unfolded Banach-Mazur game we can show that determinacy of Γ (for Γ with sufficient closure properties) implies that every set of reals that is the projection of a set in Γ has the property of Baire. So for example the existence of a measurable cardinal implies Π11 determinacy, which in turn implies that every Σ12 set of reals has the property of Baire.
By considering other games, we can show that Π1n determinacy implies that every Σ1n+1 set of reals has the property of Baire, is Lebesgue measurable (in fact universally measurable) and has the perfect set property
Perfect set property
In descriptive set theory, a subset of a Polish space has the perfect set property if it is either countable or has a nonempty perfect subset...
.
Periodicity theorems
- The first periodicity theorem implies that, for every natural number n, if Δ12n+1 determinacy holds, then Π12n+1 and Σ12n+2 have the prewellordering property (and that Σ12n+1 and Π12n+2 do not have the prewellordering property, but rather have the separation property).
- The second periodicity theorem implies that, for every natural number n, if Δ12n+1 determinacy holds, then Π12n+1 and Σ12n have the scale propertyScale propertyIn the mathematical discipline of descriptive set theory, a scale is a certain kind of object defined on a set of points in some Polish space...
. In particular, if projective determinacy holds, then every projective relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
has a projective uniformizationUniformization (set theory)In set theory, the axiom of uniformization, a weak form of the axiom of choice, states that if R is a subset of X\times Y, where X and Y are Polish spaces,...
. - The third periodicity theorem gives a sufficient condition for a game to have a definable winning strategy.
Applications to decidability of certain second-order theories
In 1969, Michael O. RabinMichael O. Rabin
Michael Oser Rabin , is an Israeli computer scientist and a recipient of the Turing Award.- Biography :Rabin was born in 1931 in Breslau, Germany, , the son of a rabbi. In 1935, he emigrated with his family to Mandate Palestine...
proved that the second-order theory
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
of n successors is decidable.
A key component of the proof requires showing determinacy of parity game
Parity game
A parity game is played on a colored directed graph, where each node has been colored by a priority – one of finitely many natural numbers. Two players, 0 and 1, take turns moving a token along the edges of the graph, resulting in a path, called the play.The winner of a finite play is the...
s, which lie in the third
level of the Borel hierarchy
Borel hierarchy
In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
.
Wadge determinacy
Wadge determinacy is the statement that for all pairs A,B of subsets of Baire spaceBaire space (set theory)
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
, the Wadge game
Wadge hierarchy
In descriptive set theory, Wadge degrees are levels of complexity for sets of reals. Sets are compared by continuous reductions. The Wadge hierarchy is the structure of Wadge degrees.- Wadge degrees :...
G(A,B) is determined. Similarly for a pointclass
Pointclass
In the mathematical field of descriptive set theory, a pointclass is a collection of sets of points, where a point is ordinarily understood to be an element of some perfect Polish space. In practice, a pointclass is usually characterized by some sort of definability property; for example, the...
Γ, Γ Wadge determinacy is the statement that for all sets A,B in Γ, the Wadge game G(A,B) is determined.
Wadge determinacy implies the semilinear ordering principle
Wadge hierarchy
In descriptive set theory, Wadge degrees are levels of complexity for sets of reals. Sets are compared by continuous reductions. The Wadge hierarchy is the structure of Wadge degrees.- Wadge degrees :...
for the Wadge order
Wadge hierarchy
In descriptive set theory, Wadge degrees are levels of complexity for sets of reals. Sets are compared by continuous reductions. The Wadge hierarchy is the structure of Wadge degrees.- Wadge degrees :...
. Another consequence of Wadge determinacy is the perfect set property
Perfect set property
In descriptive set theory, a subset of a Polish space has the perfect set property if it is either countable or has a nonempty perfect subset...
.
In general, Γ Wadge determinacy is a consequence of the determinacy of Boolean combinations of sets in Γ. In the projective hierarchy, Π11 Wadge determinacy is equivalent to Π11 determinacy, as proved by Harrington. This result was extendend by Hjorth to prove that Π12 Wadge determinacy (and in fact the semilinear ordering principle for Π12) already implies Π12 determinacy.
- This subsection is still incomplete
Games in which the objects played are not natural numbers
- This subsection is still to be written
Games played on trees
- This subsection is still to be written
Games of imperfect information
In any interesting game with imperfect information, a winning strategy will be a mixed strategy: that is, it will give some probability of differing responses to the same situation. If both players' optimal strategies are mixed strategies then the outcome of the game cannot be certainly determinant (as it can for pure strategies, since these are deterministic). But the probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
distribution of outcomes to opposing mixed strategies can be calculated. A game that requires mixed strategies is defined as determined if a strategy exists that yields a minimum expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
(over possible counter-strategies) that exceeds a given value. Against this definition, all finite two player zero-sum games are clearly determined. However, the determinacy of infinite games of imperfect information (Blackwell games) is less clear.
In 1969 David Blackwell
David Blackwell
-Honors and awards:*President, Institute of Mathematical Statistics, 1956*National Academy of Sciences, 1965*American Academy of Arts and Sciences, 1968*Honorary Fellow, Royal Statistical Society, 1976*Vice President, American Statistical Association, 1978...
proved that some "infinite games with imperfect information" (now called "Blackwell games") are determined, and in 1998 Donald A. Martin
Donald A. Martin
Donald A. Martin is a set theorist and philosopher of mathematics at UCLA, where he is a member of the faculty of mathematics and philosophy....
proved that ordinary (perfect-information game) determinacy for a boldface pointclass implies Blackwell determinacy for the pointclass. This, combined with the Borel determinacy theorem of Martin, implies that all Blackwell games with Borel payoff functions are determined.
Martin conjectured that ordinary determinacy and Blackwell determinacy for infinite games are equivalent in a strong sense (i.e. that Blackwell determinacy for a boldface pointclass in turn implies ordinary determinacy for that pointclass), but as of 2010, it has not been proven that Blackwell determinacy implies perfect-information-game determinacy.
Footnotes
- This assumes that I is trying to get the intersection of neighborhoods played to be a singleton whose unique element is an element of A. Some authors make that the goal instead for player II; that usage requires modifying the above remarks accordingly.