
Autonomous convergence theorem
Encyclopedia
In mathematics
, an autonomous convergence theorem is one of a family of related theorems
which specify conditions guaranteeing global asymptotic stability
of a continuous
autonomous
dynamical system
.
was formulated as an attempt to give conditions for global stability of continuous dynamical systems in two dimension
s. However, the Markus-Yamabe conjecture does not hold for dimensions higher than two, a problem which autonomous convergence theorems attempt to address. The first autonomous convergence theorem was constructed by Russell Smith. This theorem was later refined by Michael Li and James Muldowney.
The key point in the example theorem given above is the existence of a negative logarithmic norm, which is derived from a vector norm
. The vector norm effectively measures the distance between points in the vector space on which the differential equation is defined, and the negative logarithmic norm means that distances between points, as measured by the corresponding vector norm, are decreasing with time under the action of . So long as the trajectories
. So long as the trajectories
of all points in the phase space
are bounded
, all trajectories must therefore eventually converge to the same point.
The autonomous convergence theorems by Russell Smith, Michael Li and James Muldowney work in a similar manner, but they rely on showing that the area of two-dimensional shapes in phase space decrease with time. This means that no periodic orbits
can exist, as all closed loops must shrink to a point. If the system is bounded, then according to Pugh's closing lemma
there can be no chaotic behaviour
either, so all trajectories must eventually reach an equilibrium.
Michael Li has also developed an extended autonomous convergence theorem which is applicable to dynamical systems containing an invariant
manifold
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an autonomous convergence theorem is one of a family of related theorems
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
which specify conditions guaranteeing global asymptotic stability
Asymptotic stability
In control theory, a continuous linear time-invariant system is exponentially stable if and only if the system has eigenvalues with strictly negative real parts....
of a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
autonomous
Autonomous system (mathematics)
In mathematics, an autonomous system or autonomous differential equation is a system of ordinary differential equations which does not explicitly depend on the independent variable...
dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
.
History
The Markus-Yamabe conjectureMarkus-Yamabe conjecture
In mathematics, the Markus-Yamabe conjecture is a conjecture on global asymptotic stability. The conjecture states that if a continuously differentiable map on an n-dimensional real vector space has a single fixed point, and its Jacobian matrix is everywhere Hurwitz, then the fixed point is...
was formulated as an attempt to give conditions for global stability of continuous dynamical systems in two dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s. However, the Markus-Yamabe conjecture does not hold for dimensions higher than two, a problem which autonomous convergence theorems attempt to address. The first autonomous convergence theorem was constructed by Russell Smith. This theorem was later refined by Michael Li and James Muldowney.
An example autonomous convergence theorem
A comparatively simple autonomous convergence theorem is as follows:- Let
 be a vectorVector (mathematics and physics)In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
be a vectorVector (mathematics and physics)In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
in some space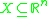 , evolving according to an autonomousAutonomous system (mathematics)In mathematics, an autonomous system or autonomous differential equation is a system of ordinary differential equations which does not explicitly depend on the independent variable...
, evolving according to an autonomousAutonomous system (mathematics)In mathematics, an autonomous system or autonomous differential equation is a system of ordinary differential equations which does not explicitly depend on the independent variable...
differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
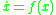 . Suppose that
. Suppose that 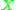 is convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
is convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
and forward invariantInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under , and that there exists a fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, and that there exists a fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
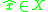 such that
such that 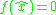 . If there exists a logarithmic normLogarithmic normIn mathematics, the logarithmic norm is a real-valued functional on operators, and is derived from either an inner product, a vector norm, or its induced operator norm. The logarithmic norm was independently introduced by Germund Dahlquist and Sergei Lozinskiĭ in 1958, for square matrices. It has...
. If there exists a logarithmic normLogarithmic normIn mathematics, the logarithmic norm is a real-valued functional on operators, and is derived from either an inner product, a vector norm, or its induced operator norm. The logarithmic norm was independently introduced by Germund Dahlquist and Sergei Lozinskiĭ in 1958, for square matrices. It has...
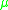 such that the JacobianJacobianIn vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
such that the JacobianJacobianIn vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
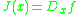 satisfies
satisfies 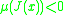 for all values of
for all values of  , then
, then 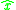 is the only fixed point, and it is globally asymptotically stable.
is the only fixed point, and it is globally asymptotically stable.
How autonomous convergence works
Note: this is an intuitive description of how autonomous convergence theorems guarantee stability, not a strictly mathematical description.The key point in the example theorem given above is the existence of a negative logarithmic norm, which is derived from a vector norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
. The vector norm effectively measures the distance between points in the vector space on which the differential equation is defined, and the negative logarithmic norm means that distances between points, as measured by the corresponding vector norm, are decreasing with time under the action of
 . So long as the trajectories
. So long as the trajectoriesTrajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
of all points in the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
are bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
, all trajectories must therefore eventually converge to the same point.
The autonomous convergence theorems by Russell Smith, Michael Li and James Muldowney work in a similar manner, but they rely on showing that the area of two-dimensional shapes in phase space decrease with time. This means that no periodic orbits
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
can exist, as all closed loops must shrink to a point. If the system is bounded, then according to Pugh's closing lemma
Pugh's closing lemma
In mathematics, Pugh's closing lemma is a result that links periodic orbit solutions of differential equations to chaotic behaviour. It can be formally stated as follows:-Interpretation:...
there can be no chaotic behaviour
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
either, so all trajectories must eventually reach an equilibrium.
Michael Li has also developed an extended autonomous convergence theorem which is applicable to dynamical systems containing an invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.

