Asymptotic stability
Encyclopedia
In control theory
, a continuous linear time-invariant system
is exponentially stable if and only if the system has eigenvalues (i.e., the poles of input-to-output systems) with strictly negative real parts. (i.e., in the left half of the complex plane
). A discrete-time input-to-output LTI system is exponentially stable if and only if the poles of its transfer function lie strictly within the unit circle centered on the origin of the complex plane. Exponential stability is a form of asymptotic stability
. Systems that are not LTI are exponentially stable if their convergence is bounded
by exponential decay
.
), then any resulting oscillations in the output will decay at an exponential rate
, and the output will tend asymptotically
to a new final, steady-state value. If the system is instead given a Dirac delta impulse
as input, then induced oscillations will die away and the system will return to its previous value. If oscillations do not die away, or the system does not return to its original output when an impulse is applied, the system is instead marginally stable
.
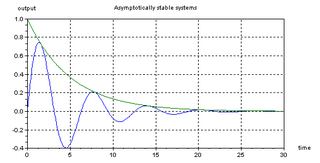The graph on the right shows the impulse response
of two similar systems. The green curve is the response of the system with impulse response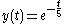
, while the blue represents the system 
. Although one response is oscillatory, both return to the original value of 0 over time.
. The marble will roll back and forth but eventually resettle in the bottom of the ladle. Drawing the horizontal position of the marble over time would give a gradually diminishing sinusoid rather like the blue curve in the image above.
A step input in this case requires supporting the marble away from the bottom of the ladle, so that it cannot roll back. It will stay in the same position and will not, as would be the case if the system were only marginally stable or entirely unstable, continue to move away from the bottom of the ladle under this constant force equal to its weight.
It is important to note that in this example the system is not stable for all inputs. Give the marble a big enough push, and it will fall out of the ladle and fall, stopping only when it reaches the floor. For some systems, therefore, it is proper to state that a system is exponentially stable over a certain range of inputs.
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, a continuous linear time-invariant system
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
is exponentially stable if and only if the system has eigenvalues (i.e., the poles of input-to-output systems) with strictly negative real parts. (i.e., in the left half of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
). A discrete-time input-to-output LTI system is exponentially stable if and only if the poles of its transfer function lie strictly within the unit circle centered on the origin of the complex plane. Exponential stability is a form of asymptotic stability
Asymptotic stability
In control theory, a continuous linear time-invariant system is exponentially stable if and only if the system has eigenvalues with strictly negative real parts....
. Systems that are not LTI are exponentially stable if their convergence is bounded
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
by exponential decay
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
.
Practical consequences
An exponentially stable LTI system is one that will not "blow up" (i.e., give an unbounded output) when given a finite input or non-zero initial condition. Moreover, if the system is given a fixed, finite input (i.e., a stepHeaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
), then any resulting oscillations in the output will decay at an exponential rate
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
, and the output will tend asymptotically
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
to a new final, steady-state value. If the system is instead given a Dirac delta impulse
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
as input, then induced oscillations will die away and the system will return to its previous value. If oscillations do not die away, or the system does not return to its original output when an impulse is applied, the system is instead marginally stable
Marginal stability
In the theory of dynamical systems, and control theory, a continuous linear time-invariant system is marginally stable if and only if the real part of every eigenvalue in the system's transfer-function is non-positive, and all eigenvalues with zero real value are simple roots...
.
Example exponentially stable LTI systems
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
of two similar systems. The green curve is the response of the system with impulse response
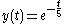, while the blue represents the system . Although one response is oscillatory, both return to the original value of 0 over time.Real-world example
Imagine putting a marble in a ladle. It will settle itself into the lowest point of the ladle and, unless disturbed, will stay there. Now imagine giving the ball a push, which is an approximation to a Dirac delta impulseDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. The marble will roll back and forth but eventually resettle in the bottom of the ladle. Drawing the horizontal position of the marble over time would give a gradually diminishing sinusoid rather like the blue curve in the image above.
A step input in this case requires supporting the marble away from the bottom of the ladle, so that it cannot roll back. It will stay in the same position and will not, as would be the case if the system were only marginally stable or entirely unstable, continue to move away from the bottom of the ladle under this constant force equal to its weight.
It is important to note that in this example the system is not stable for all inputs. Give the marble a big enough push, and it will fall out of the ladle and fall, stopping only when it reaches the floor. For some systems, therefore, it is proper to state that a system is exponentially stable over a certain range of inputs.
External links
- Parameter estimation and asymptotic stability instochastic filtering, Anastasia Papavasiliou∗September 28, 2004