
Markus-Yamabe conjecture
Encyclopedia
In mathematics
, the Markus-Yamabe conjecture is a conjecture
on global asymptotic stability
. The conjecture states that if a continuously differentiable
map on an -dimensional real
-dimensional real
vector space
has a single fixed point
, and its Jacobian matrix is everywhere Hurwitz
, then the fixed point is globally stable.
The conjecture is true for the two-dimensional case. However, counterexamples have been constructed in higher dimensions. Hence, in the two-dimensional case only, it can also be referred to as the Markus-Yamabe theorem.
Related mathematical results concerning global asymptotic stability, which are applicable in dimensions higher than two, include various autonomous convergence theorem
s. A modified version of the Markus-Yamabe conjecture has been proposed, but at present this new conjecture remains unproven.
The conjecture is true for and false in general for
and false in general for  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Markus-Yamabe conjecture is a conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
on global asymptotic stability
Asymptotic stability
In control theory, a continuous linear time-invariant system is exponentially stable if and only if the system has eigenvalues with strictly negative real parts....
. The conjecture states that if a continuously differentiable
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
map on an
 -dimensional real
-dimensional realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
has a single fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, and its Jacobian matrix is everywhere Hurwitz
Hurwitz matrix
-Hurwitz matrix and the Hurwitz stability criterion:In mathematics, Hurwitz matrix is a structured real square matrix constructed with coefficientsof a real polynomial...
, then the fixed point is globally stable.
The conjecture is true for the two-dimensional case. However, counterexamples have been constructed in higher dimensions. Hence, in the two-dimensional case only, it can also be referred to as the Markus-Yamabe theorem.
Related mathematical results concerning global asymptotic stability, which are applicable in dimensions higher than two, include various autonomous convergence theorem
Autonomous convergence theorem
In mathematics, an autonomous convergence theorem is one of a family of related theorems which specify conditions guaranteeing global asymptotic stability of a continuous autonomous dynamical system.-History:...
s. A modified version of the Markus-Yamabe conjecture has been proposed, but at present this new conjecture remains unproven.
Mathematical statement of conjecture
- Let
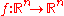 be a
be a 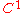 map with
map with 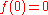 and Jacobian
and Jacobian 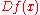 which is Hurwitz stable for every
which is Hurwitz stable for every  .
.
- Then
 is a global attractor of the dynamical system
is a global attractor of the dynamical system 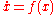 .
.
The conjecture is true for
 and false in general for
and false in general for  .
.

