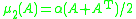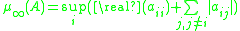Logarithmic norm
Encyclopedia
In mathematics, the logarithmic norm is a real-valued functional
on operators, and is derived from either an inner product, a vector norm, or its induced operator norm
. The logarithmic norm was independently introduced by Germund Dahlquist
and Sergei Lozinskiĭ in 1958, for square matrices
. It has since been extended to nonlinear operators and unbounded operators
as well. The logaritmic norm has a wide range of applications, in particular in matrix theory, differential equations
and numerical analysis
.
 be a square matrix and
be a square matrix and  be an induced matrix norm. The associated logarithmic norm
be an induced matrix norm. The associated logarithmic norm 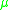 of
of  is defined
is defined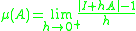
Here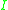 is the identity matrix
is the identity matrix
of the same dimension as , and
, and  is a real, positive number. The limit as
is a real, positive number. The limit as 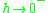 equals
equals 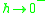 , and is in general different from the logarithmic norm
, and is in general different from the logarithmic norm  , as
, as 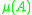 for all matrices.
for all matrices.
The matrix norm is always positive if
is always positive if 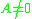 , but the logarithmic norm
, but the logarithmic norm 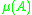 may also take negative values, e.g. when
may also take negative values, e.g. when  is negative definite
is negative definite
. Therefore, the logarithmic norm does not satisfy the axioms of a norm. The name logarithmic norm, which does not appear in the original reference, seems to originate from estimating the logarithm of the norm of solutions to the differential equation
The maximal growth rate of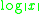 is
is  . This is expressed by the differential inequality
. This is expressed by the differential inequality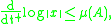
where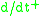 is the upper right Dini derivative
is the upper right Dini derivative
. Using logarithmic differentiation the differential inequality can also be written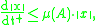
showing its direct relation to Grönwall's lemma
.
, then the logarithmic norm is the smallest number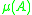 such that for all
such that for all 
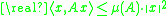
Unlike the original definition, the latter expression also allows to be unbounded. Thus differential operators
to be unbounded. Thus differential operators
too can have logarithmic norms, allowing the use of the logarithmic norm both in algebra and in analysis. The modern, extended theory therefore prefers a definition based on inner products or duality
. Both the operator norm and the logarithmic norm are then associated with extremal values of quadratic forms
as follows: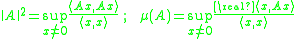
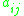 represents the element on the
represents the element on the 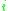 th row and
th row and 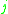 th column of a matrix
th column of a matrix 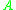 .
.
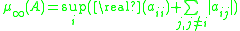
and both extreme values are taken for some vectors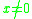 . This also means that every eigenvalue
. This also means that every eigenvalue 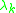 of
of 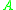 satisfies
satisfies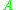 .
.
More generally, the logarithmic norm is related to the numerical range
of a matrix.
A matrix with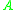 is positive definite, and one with
is positive definite, and one with 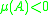 is negative definite. Such matrices have inverses. The inverse of a negative definite matrix is bounded by
is negative definite. Such matrices have inverses. The inverse of a negative definite matrix is bounded by
Both the bounds on the inverse and on the eigenvalues hold irrespective of the choice of vector (matrix) norm. Some results only hold for inner product norms, however. For example, if is a rational function with the property
is a rational function with the property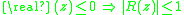
then, for inner product norms,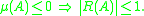
Thus the matrix norm and logarithmic norms may be viewed as generalizing the modulus and real part, respectively, from complex numbers to matrices.
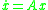 . Its role is analogous to that of the matrix norm for a discrete dynamical system
. Its role is analogous to that of the matrix norm for a discrete dynamical system 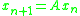 .
.
In the simplest case, when is a scalar complex constant
is a scalar complex constant  , the discrete dynamical system has stable solutions when
, the discrete dynamical system has stable solutions when  , while the differential equation has stable solutions when
, while the differential equation has stable solutions when 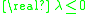 . When
. When 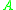 is a matrix, the discrete system has stable solutions if
is a matrix, the discrete system has stable solutions if 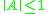 . In the continuous system, the solutions are of the form
. In the continuous system, the solutions are of the form 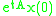 . They are stable if
. They are stable if 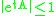 for all
for all 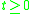 , which follows from property 7 above, if
, which follows from property 7 above, if 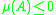 . In the latter case,
. In the latter case, 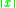 is a Lyapunov function
is a Lyapunov function
for the system.
Runge-Kutta methods for the numerical solution of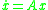 replace the differential equation by a discrete equation
replace the differential equation by a discrete equation 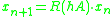 , where the rational function
, where the rational function 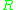 is characteristic of the method, and
is characteristic of the method, and  is the time step size. If
is the time step size. If  whenever
whenever 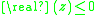 , then a stable differential equation, having
, then a stable differential equation, having 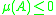 , will always result in a stable (contractive) numerical method, as
, will always result in a stable (contractive) numerical method, as 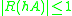 . Runge-Kutta methods having this property are called A-stable.
. Runge-Kutta methods having this property are called A-stable.
Retaining the same form, the results can, under additional assumptions, be extended to nonlinear systems as well as to semigroup
theory, where the crucial advantage of the logarithmic norm is that it discriminates between forward and reverse time evolution and can establish whether the problem is well posed
. Similar results also apply in the stability analysis in control theory
, where there is a need to discriminate between positive and negative feedback.
. In the simplest case we consider functions satisfying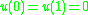 with inner product
with inner product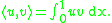
Then it holds that
where the equality on the left represents integration by parts, and the inequality to the right is a Sobolev inequality. In the latter, equality is attained for the function , implying that the constant
, implying that the constant 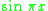 is the best possible. Thus
is the best possible. Thus
for the differential operator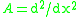 , which implies that
, which implies that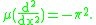
As an operator satisfying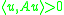 is called elliptic
is called elliptic
, the logarithmic norm quantifies the (strong) ellipticity of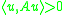 . Thus, if
. Thus, if 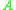 is strongly elliptic, then
is strongly elliptic, then 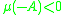 , and is invertible given proper data.
, and is invertible given proper data.
If a finite difference method is used to solve , the problem is replaced by an algebraic equation
, the problem is replaced by an algebraic equation  . The matrix
. The matrix  will typically inherit the ellipticity, i.e.,
will typically inherit the ellipticity, i.e., 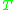 , showing that
, showing that  is positive definite and therefore invertible.
is positive definite and therefore invertible.
These results carry over to the Poisson equation
as well as to other numerical methods such as the Finite element method
.
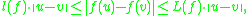
where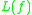 is the least upper bound Lipschitz constant
is the least upper bound Lipschitz constant
of , and
, and 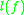 is the greatest lower bound Lipschitz constant; and
is the greatest lower bound Lipschitz constant; and
where and
and  are in the domain
are in the domain 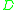 of
of 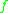 . Here
. Here 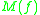 is the least upper bound logarithmic Lipschitz constant of
is the least upper bound logarithmic Lipschitz constant of 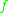 , and
, and 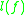 is the greatest lower bound logarithmic Lipschitz constant. It holds that
is the greatest lower bound logarithmic Lipschitz constant. It holds that 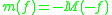 (compare above) and, analogously,
(compare above) and, analogously,  , where
, where 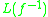 is defined on the image of
is defined on the image of 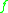 .
.
For nonlinear operators that are Lipschitz continuous, it further holds that
If is differentiable and its domain
is differentiable and its domain  is convex, then
is convex, then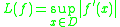 and
and 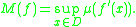
Here is the Jacobian matrix of
is the Jacobian matrix of 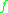 , linking the nonlinear extension to the matrix norm and logarithmic norm.
, linking the nonlinear extension to the matrix norm and logarithmic norm.
An operator having either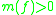 or
or 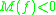 is called uniformly monotone. An operator satisfying
is called uniformly monotone. An operator satisfying 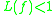 is called contractive
is called contractive
. This extension offers many connections to fixed point theory, and critical point theory.
The theory becomes analogous to that of the logarithmic norm for matrices, but is more complicated as the domains of the operators need to be given close attention, as in the case with unbounded operators. Property 8 of the logarithmic norm above carries over, independently of the choice of vector norm, and it holds that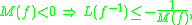
which quantifies the Uniform Monotonicity Theorem
due to Browder & Minty (1963).
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
on operators, and is derived from either an inner product, a vector norm, or its induced operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
. The logarithmic norm was independently introduced by Germund Dahlquist
Germund Dahlquist
Germund Dahlquist was a Swedish mathematician known primarily for his early contributions to the theory of numerical analysis as applied to differential equations....
and Sergei Lozinskiĭ in 1958, for square matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. It has since been extended to nonlinear operators and unbounded operators
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
as well. The logaritmic norm has a wide range of applications, in particular in matrix theory, differential equations
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
and numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
.
Original Definition
Let be a square matrix and
be a square matrix and  be an induced matrix norm. The associated logarithmic norm
be an induced matrix norm. The associated logarithmic norm 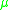 of
of 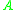 is defined
is defined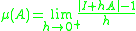
Here
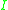 is the identity matrix
is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
of the same dimension as
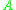 , and
, and  is a real, positive number. The limit as
is a real, positive number. The limit as 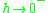 equals
equals 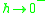 , and is in general different from the logarithmic norm
, and is in general different from the logarithmic norm  , as
, as 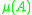 for all matrices.
for all matrices.The matrix norm
 is always positive if
is always positive if 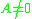 , but the logarithmic norm
, but the logarithmic norm 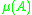 may also take negative values, e.g. when
may also take negative values, e.g. when  is negative definite
is negative definitePositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
. Therefore, the logarithmic norm does not satisfy the axioms of a norm. The name logarithmic norm, which does not appear in the original reference, seems to originate from estimating the logarithm of the norm of solutions to the differential equation

The maximal growth rate of
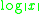 is
is  . This is expressed by the differential inequality
. This is expressed by the differential inequality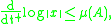
where
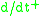 is the upper right Dini derivative
is the upper right Dini derivativeDini derivative
In mathematics and, specifically, real analysis, the Dini derivatives are a class of generalizations of the derivative...
. Using logarithmic differentiation the differential inequality can also be written
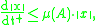
showing its direct relation to Grönwall's lemma
Grönwall's inequality
In mathematics, Gronwall's lemma or Grönwall's lemma, also called Gronwall–Bellman inequality, allows one to bound a function that is known to satisfy a certain differential or integral inequality by the solution of the corresponding differential or integral equation. There are two forms of the...
.
Alternative definitions
If the vector norm is an inner product norm, as in a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, then the logarithmic norm is the smallest number
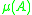 such that for all
such that for all 
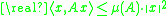
Unlike the original definition, the latter expression also allows
 to be unbounded. Thus differential operators
to be unbounded. Thus differential operatorsDifferential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
too can have logarithmic norms, allowing the use of the logarithmic norm both in algebra and in analysis. The modern, extended theory therefore prefers a definition based on inner products or duality
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
. Both the operator norm and the logarithmic norm are then associated with extremal values of quadratic forms
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
as follows:
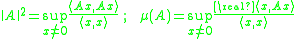
Properties
Basic properties of the logarithmic norm of a matrix include:-
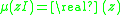
-

-
 for scalar
for scalar 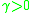
-
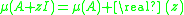
-
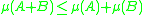
-
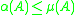 where
where 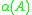 is the maximal real part of the eigenvaluesEigenvalue, eigenvector and eigenspaceThe eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
is the maximal real part of the eigenvaluesEigenvalue, eigenvector and eigenspaceThe eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
of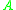
-
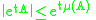 for
for 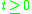
-
Example logarithmic norms
The logarithmic norm of a matrix can be calculated as follows for the three most common norms. In these formulas,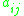 represents the element on the
represents the element on the 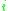 th row and
th row and 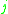 th column of a matrix
th column of a matrix 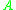 .
.Applications in matrix theory and spectral theory
The logarithmic norm is related to the extreme values of the Rayleigh quotient. It holds that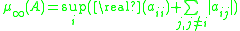
and both extreme values are taken for some vectors
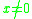 . This also means that every eigenvalue
. This also means that every eigenvalue 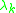 of
of 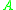 satisfies
satisfies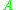 .
.More generally, the logarithmic norm is related to the numerical range
Numerical range
In the mathematical field of linear algebra and convex analysis, the numerical range of a square matrix with complex entries is a subset of the complex plane associated to the matrix...
of a matrix.
A matrix with
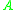 is positive definite, and one with
is positive definite, and one with 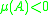 is negative definite. Such matrices have inverses. The inverse of a negative definite matrix is bounded by
is negative definite. Such matrices have inverses. The inverse of a negative definite matrix is bounded by
Both the bounds on the inverse and on the eigenvalues hold irrespective of the choice of vector (matrix) norm. Some results only hold for inner product norms, however. For example, if
 is a rational function with the property
is a rational function with the property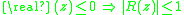
then, for inner product norms,
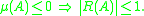
Thus the matrix norm and logarithmic norms may be viewed as generalizing the modulus and real part, respectively, from complex numbers to matrices.
Applications in stability theory and numerical analysis
The logarithmic norm plays an important role in the stability analysis of a continuous dynamical system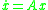 . Its role is analogous to that of the matrix norm for a discrete dynamical system
. Its role is analogous to that of the matrix norm for a discrete dynamical system 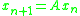 .
.In the simplest case, when
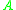 is a scalar complex constant
is a scalar complex constant 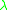 , the discrete dynamical system has stable solutions when
, the discrete dynamical system has stable solutions when  , while the differential equation has stable solutions when
, while the differential equation has stable solutions when 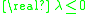 . When
. When 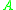 is a matrix, the discrete system has stable solutions if
is a matrix, the discrete system has stable solutions if 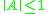 . In the continuous system, the solutions are of the form
. In the continuous system, the solutions are of the form 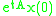 . They are stable if
. They are stable if 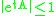 for all
for all 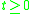 , which follows from property 7 above, if
, which follows from property 7 above, if 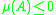 . In the latter case,
. In the latter case, 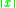 is a Lyapunov function
is a Lyapunov functionLyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
for the system.
Runge-Kutta methods for the numerical solution of
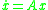 replace the differential equation by a discrete equation
replace the differential equation by a discrete equation 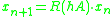 , where the rational function
, where the rational function 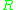 is characteristic of the method, and
is characteristic of the method, and 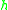 is the time step size. If
is the time step size. If  whenever
whenever 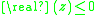 , then a stable differential equation, having
, then a stable differential equation, having 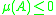 , will always result in a stable (contractive) numerical method, as
, will always result in a stable (contractive) numerical method, as 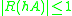 . Runge-Kutta methods having this property are called A-stable.
. Runge-Kutta methods having this property are called A-stable.Retaining the same form, the results can, under additional assumptions, be extended to nonlinear systems as well as to semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
theory, where the crucial advantage of the logarithmic norm is that it discriminates between forward and reverse time evolution and can establish whether the problem is well posed
Well-posed problem
The mathematical term well-posed problem stems from a definition given by Jacques Hadamard. He believed that mathematical models of physical phenomena should have the properties that# A solution exists# The solution is unique...
. Similar results also apply in the stability analysis in control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, where there is a need to discriminate between positive and negative feedback.
Applications to elliptic differential operators
In connection with differential operators it is common to use inner products and integration by partsIntegration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
. In the simplest case we consider functions satisfying
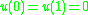 with inner product
with inner product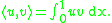
Then it holds that

where the equality on the left represents integration by parts, and the inequality to the right is a Sobolev inequality. In the latter, equality is attained for the function
 , implying that the constant
, implying that the constant 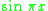 is the best possible. Thus
is the best possible. Thus
for the differential operator
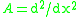 , which implies that
, which implies that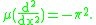
As an operator satisfying
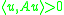 is called elliptic
is called ellipticElliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
, the logarithmic norm quantifies the (strong) ellipticity of
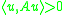 . Thus, if
. Thus, if 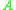 is strongly elliptic, then
is strongly elliptic, then 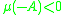 , and is invertible given proper data.
, and is invertible given proper data.If a finite difference method is used to solve
 , the problem is replaced by an algebraic equation
, the problem is replaced by an algebraic equation  . The matrix
. The matrix  will typically inherit the ellipticity, i.e.,
will typically inherit the ellipticity, i.e., 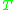 , showing that
, showing that  is positive definite and therefore invertible.
is positive definite and therefore invertible.These results carry over to the Poisson equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
as well as to other numerical methods such as the Finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
.
Extensions to nonlinear maps
For nonlinear operators the operator norm and logarithmic norm are defined in terms of the inequalities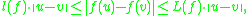
where
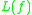 is the least upper bound Lipschitz constant
is the least upper bound Lipschitz constantLipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
of
 , and
, and 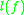 is the greatest lower bound Lipschitz constant; and
is the greatest lower bound Lipschitz constant; and
where
 and
and  are in the domain
are in the domain 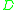 of
of 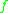 . Here
. Here 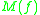 is the least upper bound logarithmic Lipschitz constant of
is the least upper bound logarithmic Lipschitz constant of 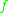 , and
, and 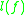 is the greatest lower bound logarithmic Lipschitz constant. It holds that
is the greatest lower bound logarithmic Lipschitz constant. It holds that 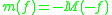 (compare above) and, analogously,
(compare above) and, analogously,  , where
, where 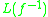 is defined on the image of
is defined on the image of 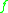 .
.For nonlinear operators that are Lipschitz continuous, it further holds that

If
 is differentiable and its domain
is differentiable and its domain  is convex, then
is convex, then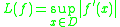 and
and 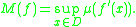
Here
 is the Jacobian matrix of
is the Jacobian matrix of 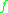 , linking the nonlinear extension to the matrix norm and logarithmic norm.
, linking the nonlinear extension to the matrix norm and logarithmic norm.An operator having either
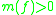 or
or 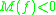 is called uniformly monotone. An operator satisfying
is called uniformly monotone. An operator satisfying 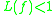 is called contractive
is called contractiveContraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
. This extension offers many connections to fixed point theory, and critical point theory.
The theory becomes analogous to that of the logarithmic norm for matrices, but is more complicated as the domains of the operators need to be given close attention, as in the case with unbounded operators. Property 8 of the logarithmic norm above carries over, independently of the choice of vector norm, and it holds that
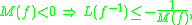
which quantifies the Uniform Monotonicity Theorem
Browder-Minty theorem
In mathematics, the Browder–Minty theorem states that a bounded, continuous, coercive and monotone function T from a real, separable reflexive Banach space X into its continuous dual space X∗ is automatically surjective...
due to Browder & Minty (1963).