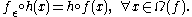Axiom A
Encyclopedia
In mathematics
, Smale's axiom A defines a class of dynamical system
s which have been extensively studied and whose dynamics is relatively well understood. A prominent example is the Smale horseshoe map. The term "axiom A" originates with Stephen Smale
. The importance of such systems is demonstrated by the chaotic hypothesis, which states that, 'for all practical purposes', that a many-body thermostatted system is approximated by an Anosov system.
f: M→M. Then f is an axiom A diffeomorphism if
the following two conditions hold:
For surfaces, hyperbolicity of the nonwandering set implies the density of periodic points, but this is no longer true in higher dimensions. Nonetheless, axiom A diffeomorphisms are sometimes called hyperbolic diffeomorphisms, because the portion of M where the interesting dynamics occurs, namely, Ω(f), exhibits hyperbolic behavior.
Axiom A diffeomorphisms generalize Morse–Smale system
s, which satisfy further restrictions (finitely many periodic points and transversality of stable and unstable submanifolds). Smale horseshoe map is an axiom A diffeomorphism with infinitely many periodic points and positive topological entropy
.
satisfies axiom A. In this case, the whole manifold M is hyperbolic (although it is an open question whether the non-wandering set Ω(f) constitutes the whole M).
Rufus Bowen
showed that the non-wandering set Ω(f) of any axiom A diffeomorphism supports a Markov partition
. Thus the restriction of f to a certain generic subset of Ω(f) is conjugated to a shift of finite type.
The density of the periodic points in the non-wandering set implies its local maximality: there exists an open neighborhood U of Ω(f) such that
More precisely, for every C1-perturbation
fε of f, its non-wandering set is formed by two compact, fε-invariant subsets Ω1 and Ω2. The first subset is homeomorphic to Ω(f) via a homeomorphism
h which conjugates the restriction of f to Ω(f) with the restriction of fε to Ω1:
If Ω2 is empty then h is onto Ω(fε). If this is the case for every perturbation fε then f is called omega stable. A diffeomorphism f is omega stable if and only if it satisfies axiom A and the no-cycle condition (that an orbit, once having left an invariant subset, does not return).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Smale's axiom A defines a class of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s which have been extensively studied and whose dynamics is relatively well understood. A prominent example is the Smale horseshoe map. The term "axiom A" originates with Stephen Smale
Stephen Smale
Steven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...
. The importance of such systems is demonstrated by the chaotic hypothesis, which states that, 'for all practical purposes', that a many-body thermostatted system is approximated by an Anosov system.
Definition
Let M be a smooth manifold with a diffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
f: M→M. Then f is an axiom A diffeomorphism if
the following two conditions hold:
- The nonwandering set of f, Ω(f), is a hyperbolic setHyperbolic setIn dynamical systems theory, a subset Λ of a smooth manifold M is said to have a hyperbolic structure with respect to a smooth map f if its tangent bundle may be split into two invariant subbundles, one of which is contracting and the other is expanding under f, with respect to some...
and compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. - The set of periodic pointPeriodic pointIn mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...
s of f is dense in Ω(f).
For surfaces, hyperbolicity of the nonwandering set implies the density of periodic points, but this is no longer true in higher dimensions. Nonetheless, axiom A diffeomorphisms are sometimes called hyperbolic diffeomorphisms, because the portion of M where the interesting dynamics occurs, namely, Ω(f), exhibits hyperbolic behavior.
Axiom A diffeomorphisms generalize Morse–Smale system
Morse–Smale system
In dynamical systems theory, an area of applied mathematics, a Morse–Smale system is a smooth dynamical system whose non-wandering set consists of finitely many hyperbolic equilibrium points and hyperbolic periodic orbits and satisfying a transversality condition on the stable and unstable manifolds...
s, which satisfy further restrictions (finitely many periodic points and transversality of stable and unstable submanifolds). Smale horseshoe map is an axiom A diffeomorphism with infinitely many periodic points and positive topological entropy
Topological entropy
In mathematics, the topological entropy of a topological dynamical system is a nonnegative real number that measures the complexity of the system. Topological entropy was first introduced in 1965 by Adler, Konheim and McAndrew. Their definition was modelled after the definition of the...
.
Properties
Any Anosov diffeomorphismAnosov diffeomorphism
In mathematics, more particularly in the fields of dynamical systems and geometric topology, an Anosov map on a manifold M is a certain type of mapping, from M to itself, with rather clearly marked local directions of 'expansion' and 'contraction'. Anosov systems are a special case of Axiom A...
satisfies axiom A. In this case, the whole manifold M is hyperbolic (although it is an open question whether the non-wandering set Ω(f) constitutes the whole M).
Rufus Bowen
Rufus Bowen
Robert Edward "Rufus" Bowen was an internationally known professor in the Department of Mathematics at the University of California, Berkeley, who specialized in dynamical systems theory...
showed that the non-wandering set Ω(f) of any axiom A diffeomorphism supports a Markov partition
Markov partition
A Markov partition is a tool used in dynamical systems theory, allowing the methods of symbolic dynamics to be applied to the study of hyperbolic systems. By using a Markov partition, the system can be made to resemble a discrete-time Markov process, with the long-term dynamical characteristics...
. Thus the restriction of f to a certain generic subset of Ω(f) is conjugated to a shift of finite type.
The density of the periodic points in the non-wandering set implies its local maximality: there exists an open neighborhood U of Ω(f) such that
Omega stability
An important property of Axiom A systems is their structural stability against small perturbations. That is, trajectories of the perturbed system remain in 1-1 topological correspondence with the unperturbed system. This property is important, in that it shows that Axiom A systems are not exceptional, but are in a sense 'generic'.More precisely, for every C1-perturbation
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
fε of f, its non-wandering set is formed by two compact, fε-invariant subsets Ω1 and Ω2. The first subset is homeomorphic to Ω(f) via a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
h which conjugates the restriction of f to Ω(f) with the restriction of fε to Ω1:
If Ω2 is empty then h is onto Ω(fε). If this is the case for every perturbation fε then f is called omega stable. A diffeomorphism f is omega stable if and only if it satisfies axiom A and the no-cycle condition (that an orbit, once having left an invariant subset, does not return).