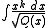Differential of the first kind
Encyclopedia
In mathematics
, differential of the first kind is a traditional term used in the theories of Riemann surface
s (more generally, complex manifold
s) and algebraic curve
s (more generally, algebraic geometry
), for everywhere-regular differential 1-forms
. Given a complex manifold M, a differential of the first kind ω is therefore the same thing as a 1-form that is everywhere holomorphic; on an algebraic variety
V that is non-singular it would be a global section of the coherent sheaf
Ω1 of Kähler differential
s. In either case the definition has its origins in the theory of abelian integrals.
The dimension of the space of differentials of the first kind, by means of this identification, is the Hodge number
The differentials of the first kind, when integrated along paths, give rise to integrals that generalise to all curves over the complex number
s the elliptic integral
s. They include for example the hyper-elliptic integrals of type
where Q is a square-free polynomial
of any given degree > 4. The allowable power k has to be determined by analysis of the possible pole at the point at infinity on the corresponding hyperelliptic curve. When this is done, one finds that the condition is
or in other words, k at most 1 for degree of Q 5 or 6, at most 2 for degree 7 or 8, and so on.
Quite generally, as this example illustrates, for a compact Riemann surface
or algebraic curve
, the Hodge number is the genus
g. For the case of algebraic surface
s, this is the quantity known classically as the irregularity
q. It is also, in general, the dimension of the Albanese variety
, which takes the place of the Jacobian variety
.
, and through the use of morphisms to commutative algebraic group
s.
The Weierstrass zeta function was called an integral of the second kind in elliptic function
theory; it is a logarithmic derivative
of a theta function, and therefore has simple poles, with integer residues. The decomposition of a (meromorphic) elliptic function into pieces of 'three kinds' parallels the representation as (i) a constant, plus (ii) a linear combination
of translates of the Weierstrass zeta function, plus (iii) a function with arbitrary poles but no residues at them.
The same type of decomposition exists in general, mutatis mutandis, though the terminology is not completely consistent. In the algebraic group (generalized Jacobian
) theory the three kinds are abelian varieties, algebraic tori, and affine space
s, and the decomposition is in terms of a composition series
.
On the other hand, a meromorphic abelian differential of the second kind has traditionally been one with residues at all poles being zero. There is a higher-dimensional analogue available, using the Poincaré residue
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, differential of the first kind is a traditional term used in the theories of Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s (more generally, complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s) and algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s (more generally, algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
), for everywhere-regular differential 1-forms
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
. Given a complex manifold M, a differential of the first kind ω is therefore the same thing as a 1-form that is everywhere holomorphic; on an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
V that is non-singular it would be a global section of the coherent sheaf
Coherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
Ω1 of Kähler differential
Kähler differential
In mathematics, Kähler differentials provide an adaptation of differential forms to arbitrary commutative rings or schemes.-Presentation:The idea was introduced by Erich Kähler in the 1930s...
s. In either case the definition has its origins in the theory of abelian integrals.
The dimension of the space of differentials of the first kind, by means of this identification, is the Hodge number
- h0,1.
The differentials of the first kind, when integrated along paths, give rise to integrals that generalise to all curves over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s the elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s. They include for example the hyper-elliptic integrals of type
where Q is a square-free polynomial
Square-free polynomial
In mathematics, a square-free polynomial is a polynomial with no square factors, i.e, f \in F[x] is square-free if and only if b^2 \nmid f for every b \in F[x] with non-zero degree. This definition implies that no factors of higher order can exist, either, for if b3 divided the polynomial, then b2...
of any given degree > 4. The allowable power k has to be determined by analysis of the possible pole at the point at infinity on the corresponding hyperelliptic curve. When this is done, one finds that the condition is
- k ≤ g − 1,
or in other words, k at most 1 for degree of Q 5 or 6, at most 2 for degree 7 or 8, and so on.
Quite generally, as this example illustrates, for a compact Riemann surface
Compact Riemann surface
In mathematics, a compact Riemann surface is a complex manifold of dimension one that is a compact space. Riemann surfaces are generally classified first into the compact and the open .A compact Riemann surface C that is a...
or algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
, the Hodge number is the genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
g. For the case of algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
s, this is the quantity known classically as the irregularity
Irregularity of a surface
In mathematics, the irregularity of a complex surface X is the Hodge number h0,1= dim H1, usually denoted by q . The irregularity of an algebraic surface is sometimes defined to be this Hodge number, and sometimes defined to be the dimension of the Picard variety , which is the same in...
q. It is also, in general, the dimension of the Albanese variety
Albanese variety
In mathematics, the Albanese variety A, named for Giacomo Albanese, is a generalization of the Jacobian variety of a curve, and is the abelian variety generated by a variety V. In other words there is a morphism from the variety V to its Albanese variety A, such that any morphism from V to an...
, which takes the place of the Jacobian variety
Jacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
.
Differentials of the second and third kind
The traditional terminology included also differentials of the second kind and of the third kind. The idea behind this has been supported by modern theories of algebraic differential forms, both from the side of more Hodge theoryHodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
, and through the use of morphisms to commutative algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s.
The Weierstrass zeta function was called an integral of the second kind in elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
theory; it is a logarithmic derivative
Logarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
of a theta function, and therefore has simple poles, with integer residues. The decomposition of a (meromorphic) elliptic function into pieces of 'three kinds' parallels the representation as (i) a constant, plus (ii) a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of translates of the Weierstrass zeta function, plus (iii) a function with arbitrary poles but no residues at them.
The same type of decomposition exists in general, mutatis mutandis, though the terminology is not completely consistent. In the algebraic group (generalized Jacobian
Generalized Jacobian
- In algebraic geometry :In mathematics, there are several notions of generalized Jacobians, which are algebraic groups or complex manifolds that are in some sense analogous to the Jacobian variety of an algebraic curve, or related to the Albanese variety and Picard variety that generalize it to...
) theory the three kinds are abelian varieties, algebraic tori, and affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
s, and the decomposition is in terms of a composition series
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
.
On the other hand, a meromorphic abelian differential of the second kind has traditionally been one with residues at all poles being zero. There is a higher-dimensional analogue available, using the Poincaré residue
Poincaré residue
In mathematics, the Poincaré residue is a generalization, to several complex variables and complex manifold theory, of the residue at a pole of complex function theory. It is just one of a number of such possible extensions....