
Acyclic space
Encyclopedia
In mathematics
, an acyclic space is a topological space
X in which cycles are always boundaries, in the sense of homology theory
. This implies that the integral homology groups in all dimensions of X are isomorphic to the corresponding homology groups of a point.
In other words, using the idea of reduced homology
,
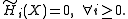
If X is an acyclic CW complex
, and if the fundamental group
of X is trivial, then X is a contractible space
, as follows from the Whitehead theorem
and the Hurewicz theorem
.
, where they can be used to construct other, more interesting topological spaces.
For example, if one removes a single point from a manifold
M which is a homology sphere
, one gets such a space. The homotopy group
s of an acyclic space X do not vanish in general, because the fundamental group need not be trivial. For example, the punctured Poincaré sphere is an acyclic, 3-dimensional manifold which is not contractible.
This gives a repertoire of examples, since the first homology group is the abelianisation of the fundamental group. With every perfect group
G one can associate a (canonical, terminal) acyclic space, whose fundamental group is a central extension of the given group G.
The homotopy groups of these associated acyclic spaces are closely related to Quillen's plus construction
on the classifying space
BG.
BG is acyclic; in other words, all its (reduced) group homology groups vanish (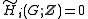 ). Every acyclic group is thus a perfect group
). Every acyclic group is thus a perfect group
(meaning first homology group vanishes: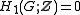 ), and in fact, a superperfect group
), and in fact, a superperfect group
(meaning first two homology groups vanish: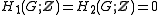 ). The converse is not true: the binary icosahedral group is superperfect (hence perfect) but not acyclic.
). The converse is not true: the binary icosahedral group is superperfect (hence perfect) but not acyclic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an acyclic space is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X in which cycles are always boundaries, in the sense of homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
. This implies that the integral homology groups in all dimensions of X are isomorphic to the corresponding homology groups of a point.
In other words, using the idea of reduced homology
Reduced homology
In mathematics, reduced homology is a minor modification made to homology theory in algebraic topology, designed to make a point have all its homology groups zero...
,
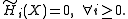
If X is an acyclic CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
, and if the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of X is trivial, then X is a contractible space
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
, as follows from the Whitehead theorem
Whitehead theorem
In homotopy theory , the Whitehead theorem states that if a continuous mapping f between topological spaces X and Y induces isomorphisms on all homotopy groups, then f is a homotopy equivalence provided X and Y are connected and have the homotopy-type of CW complexes. This result was proved by J....
and the Hurewicz theorem
Hurewicz theorem
In mathematics, the Hurewicz theorem is a basic result of algebraic topology, connecting homotopy theory with homology theory via a map known as the Hurewicz homomorphism...
.
Examples
Acyclic spaces occur in topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, where they can be used to construct other, more interesting topological spaces.
For example, if one removes a single point from a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M which is a homology sphere
Homology sphere
In algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer n ≥ 1. That is,andTherefore X is a connected space, with one non-zero higher Betti number: bn...
, one gets such a space. The homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of an acyclic space X do not vanish in general, because the fundamental group need not be trivial. For example, the punctured Poincaré sphere is an acyclic, 3-dimensional manifold which is not contractible.
This gives a repertoire of examples, since the first homology group is the abelianisation of the fundamental group. With every perfect group
Perfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
G one can associate a (canonical, terminal) acyclic space, whose fundamental group is a central extension of the given group G.
The homotopy groups of these associated acyclic spaces are closely related to Quillen's plus construction
Plus construction
In mathematics, the plus construction is a method for simplifying the fundamental group of a space without changing its homology and cohomology groups. It was introduced by Daniel Quillen. Given a perfect normal subgroup of the fundamental group of a connected CW complex X, attach two-cells along...
on the classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
BG.
Acyclic groups
An acyclic group is a group G whose classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
BG is acyclic; in other words, all its (reduced) group homology groups vanish (
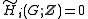 ). Every acyclic group is thus a perfect group
). Every acyclic group is thus a perfect groupPerfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
(meaning first homology group vanishes:
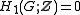 ), and in fact, a superperfect group
), and in fact, a superperfect groupSuperperfect group
In mathematics, in the realm of group theory, a group is said to be superperfect when its first two homology groups are trivial: H_1=H_2=0. This is stronger than a perfect group, which is one whose first homology group vanishes...
(meaning first two homology groups vanish:
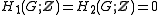 ). The converse is not true: the binary icosahedral group is superperfect (hence perfect) but not acyclic.
). The converse is not true: the binary icosahedral group is superperfect (hence perfect) but not acyclic.

