
Superperfect group
Encyclopedia
In mathematics
, in the realm of group theory
, a group
is said to be superperfect when its first two homology groups are trivial
: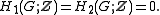 This is stronger than a perfect group, which is one whose first homology group vanishes. In more classical terms, a superperfect group is one whose abelianization and Schur multiplier
This is stronger than a perfect group, which is one whose first homology group vanishes. In more classical terms, a superperfect group is one whose abelianization and Schur multiplier
both vanish; abelianization equals the first homology, while the Schur multiplier equals the second homology.
of the group itself, since the homology of a group G is the homology of any Eilenberg-MacLane space
of type K(G,1); the fundamental group
of a K(G,1) is G, and the first homology of K(G,1) is then abelianization of its fundamental group. Thus, if a group is superperfect, then it is perfect
.
A finite perfect group is superperfect if and only if it is its own universal central extension (UCE), as the second homology group of a perfect group parametrizes central extensions.
, then G is superperfect. The smallest finite, non-trivial superperfect group is the binary icosahedral group (the fundamental group of the Poincaré
homology sphere).
The alternating group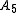 is perfect but not superperfect: it has a non-trivial central extension, the binary icosahedral group (which is in fact its UCE, and is superperfect). More generally, the projective special linear groups PSL(n,q) are simple (hence perfect) except for PSL(2,2) and PSL(2,3), but not superperfect, with the special linear group
is perfect but not superperfect: it has a non-trivial central extension, the binary icosahedral group (which is in fact its UCE, and is superperfect). More generally, the projective special linear groups PSL(n,q) are simple (hence perfect) except for PSL(2,2) and PSL(2,3), but not superperfect, with the special linear group
s SL(n,q) as central extensions. This family includes the binary icosahedral group (thought of as SL(2,5)) as UCE of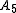 (thought of as PSL(2,5)).
(thought of as PSL(2,5)).
Every acyclic group is superperfect, but the converse is not true: the binary icosahedral group is superperfect, but not acyclic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the realm of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is said to be superperfect when its first two homology groups are trivial
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
:
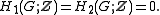 This is stronger than a perfect group, which is one whose first homology group vanishes. In more classical terms, a superperfect group is one whose abelianization and Schur multiplier
This is stronger than a perfect group, which is one whose first homology group vanishes. In more classical terms, a superperfect group is one whose abelianization and Schur multiplierSchur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
both vanish; abelianization equals the first homology, while the Schur multiplier equals the second homology.
Definition
The first homology group of a group is the abelianizationCommutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
of the group itself, since the homology of a group G is the homology of any Eilenberg-MacLane space
Eilenberg-MacLane space
In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" , and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without...
of type K(G,1); the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a K(G,1) is G, and the first homology of K(G,1) is then abelianization of its fundamental group. Thus, if a group is superperfect, then it is perfect
Perfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
.
A finite perfect group is superperfect if and only if it is its own universal central extension (UCE), as the second homology group of a perfect group parametrizes central extensions.
Examples
For example, if G is the fundamental group of a homology sphereHomology sphere
In algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer n ≥ 1. That is,andTherefore X is a connected space, with one non-zero higher Betti number: bn...
, then G is superperfect. The smallest finite, non-trivial superperfect group is the binary icosahedral group (the fundamental group of the Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
homology sphere).
The alternating group
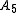 is perfect but not superperfect: it has a non-trivial central extension, the binary icosahedral group (which is in fact its UCE, and is superperfect). More generally, the projective special linear groups PSL(n,q) are simple (hence perfect) except for PSL(2,2) and PSL(2,3), but not superperfect, with the special linear group
is perfect but not superperfect: it has a non-trivial central extension, the binary icosahedral group (which is in fact its UCE, and is superperfect). More generally, the projective special linear groups PSL(n,q) are simple (hence perfect) except for PSL(2,2) and PSL(2,3), but not superperfect, with the special linear groupSpecial linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
s SL(n,q) as central extensions. This family includes the binary icosahedral group (thought of as SL(2,5)) as UCE of
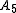 (thought of as PSL(2,5)).
(thought of as PSL(2,5)).Every acyclic group is superperfect, but the converse is not true: the binary icosahedral group is superperfect, but not acyclic.

