Wadge hierarchy
Encyclopedia
In descriptive set theory
, Wadge degrees are levels of complexity for sets of reals. Sets are compared by continuous reductions. The Wadge hierarchy is the structure of Wadge degrees.
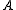and 
are subsets of Baire space
ωω.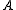
is Wadge reducible to 
or 
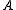≤W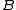 
if there is a continuous function 
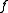on ωω with 
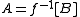. The Wadge order is the preorder
or quasiorder on the subsets of Baire space. Equivalence classes of sets under this preorder are called Wadge degrees, the degree of a set
is denoted by [
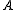]W. The set of Wadge degrees ordered by the Wadge order is called the Wadge hierarchy.
Properties of Wadge degrees include their consistency with measures of complexity stated in terms of definability. For example, if
≤W 
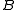and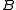 
is a countable intersection of open set
s, then so is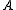
. The same works for all levels of the Borel hierarchy
and the difference hierarchy. The Wadge hierarchy plays an important role in models of the axiom of determinacy
. Further interest in Wadge degrees comes from computer science, where some papers have suggested Wadge degrees are relevant to algorithmic complexity.
discovered by William Wadge . It is used to investigate the notion of continuous reduction for subsets of Baire space. Wadge had analyzed the structure of the Wadge hierarchy for Baire space with games by 1972, but published these results only much later in his PhD thesis. In the Wadge game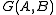
, player I and player II each in turn play integers which may depend on those played before. The outcome of the game is determined by checking whether the sequences x and y generated by players I and II are contained in the sets A and B, respectively. Player II wins if the outcome is the same for both players, i.e. 
is in 
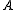if and only if 
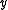is in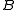 
. Player I wins if the outcome is different. Sometimes this is also called the Lipschitz game, and the variant where player II has the option to pass (but has to play infinitely often) is called the Wadge game.
Suppose for a moment that the game is determined
. If player I has a winning strategy, then this defines a continuous (even Lipschitz) map reducing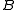
to the complement of 
, and if on the other hand player II has a winning strategy then you have a reduction of 
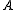to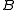 
. For example, suppose that player II has a winning strategy. Map every sequence x to the sequence y that player II plays in 
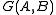if player I plays the sequence x, where player II follows his or her winning strategy. This defines a is a continuous map f with the property that x is in 
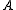if and only if f(x) is in 
.
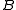Wadge's lemma states that under the axiom of determinacy
(AD
), for any two subsets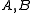
of Baire space, 
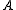≤W 
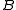or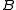 
≤W ωω–
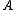. The assertion that the Wadge lemma holds for sets in Γ is the semilinear ordering principle for Γ or SLO(Γ). Any defines a linear order on the equivalence classes modulo complements. Wadge's lemma can be applied locally to any pointclass
Γ, for example the Borel sets, Δ1n sets, Σ1n sets, or Π1n sets. It follows from determinacy of differences of sets in Γ. Since Borel determinacy
is proved in ZFC, ZFC implies Wadge's lemma for Borel sets.
and Monk proved in 1973 that AD
implies the Wadge order for Baire space is well founded. Hence under AD, the Wadge classes modulo complements form a wellorder. The Wadge rank of a set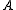
is the order type of the set of Wadge degrees modulo complements strictly below [
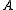]W. The length of the Wadge hierarchy has been shown to be Θ. Wadge also proved that the length of the Wadge hierarchy restricted to the Borel sets is φω1(1) (or φω1(2) depending on the notation), where φγ is the γth Veblen function
to the base ω1 (instead of the usual ω).
As for the Wadge lemma, this holds for any pointclass Γ, assuming the axiom of determinacy
. If we associate with each set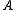
the collection of all sets strictly below 
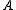on the Wadge hierarchy, this forms a pointclass. Equivalently, for each ordinal α≤θ the collection Wα of sets which show up before stage α is a pointclass
. Conversely, every pointclass is equal to some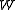
α. A pointclass is said to be self-dual if it is closed
under complementation. It can be shown that Wα is self-dual if and only if α is either 0, an even successor ordinal
, or a limit ordinal of countable cofinality
.
≤F 
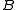if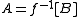 
for some function 
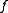in F. Any such class of functions again determines a preorder
on the subsets of Baire space. Degrees given by Lipschitz functions are called Lipschitz degrees, and degrees from Borel functions Borel-Wadge degrees.
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
, Wadge degrees are levels of complexity for sets of reals. Sets are compared by continuous reductions. The Wadge hierarchy is the structure of Wadge degrees.
Wadge degrees
Suppose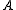 and are subsets of Baire spaceBaire space (set theory)
In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
ωω.
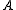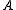is Wadge reducible to or ≤W 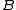if there is a continuous function 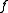on ωω with 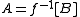. The Wadge order is the preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
or quasiorder on the subsets of Baire space. Equivalence classes of sets under this preorder are called Wadge degrees, the degree of a set
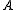is denoted by [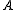]W. The set of Wadge degrees ordered by the Wadge order is called the Wadge hierarchy.Properties of Wadge degrees include their consistency with measures of complexity stated in terms of definability. For example, if
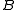≤W and 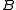is a countable intersection of open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s, then so is
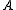. The same works for all levels of the Borel hierarchyBorel hierarchy
In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
and the difference hierarchy. The Wadge hierarchy plays an important role in models of the axiom of determinacy
Axiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
. Further interest in Wadge degrees comes from computer science, where some papers have suggested Wadge degrees are relevant to algorithmic complexity.
Wadge and Lipschitz games
The Wadge game is a simple infinite gameGame theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
discovered by William Wadge . It is used to investigate the notion of continuous reduction for subsets of Baire space. Wadge had analyzed the structure of the Wadge hierarchy for Baire space with games by 1972, but published these results only much later in his PhD thesis. In the Wadge game
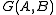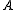, player I and player II each in turn play integers which may depend on those played before. The outcome of the game is determined by checking whether the sequences x and y generated by players I and II are contained in the sets A and B, respectively. Player II wins if the outcome is the same for both players, i.e. is in if and only if 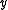is in 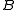. Player I wins if the outcome is different. Sometimes this is also called the Lipschitz game, and the variant where player II has the option to pass (but has to play infinitely often) is called the Wadge game.Suppose for a moment that the game is determined
Determinacy
In set theory, a branch of mathematics, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.-Games:...
. If player I has a winning strategy, then this defines a continuous (even Lipschitz) map reducing
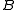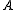to the complement of , and if on the other hand player II has a winning strategy then you have a reduction of to 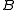. For example, suppose that player II has a winning strategy. Map every sequence x to the sequence y that player II plays in 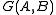if player I plays the sequence x, where player II follows his or her winning strategy. This defines a is a continuous map f with the property that x is in 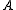if and only if f(x) is in 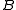.Wadge's lemma states that under the axiom of determinacy
Axiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
(AD
Axiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
), for any two subsets
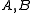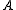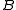of Baire space, ≤W or 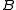≤W ωω–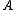. The assertion that the Wadge lemma holds for sets in Γ is the semilinear ordering principle for Γ or SLO(Γ). Any defines a linear order on the equivalence classes modulo complements. Wadge's lemma can be applied locally to any pointclassPointclass
In the mathematical field of descriptive set theory, a pointclass is a collection of sets of points, where a point is ordinarily understood to be an element of some perfect Polish space. In practice, a pointclass is usually characterized by some sort of definability property; for example, the...
Γ, for example the Borel sets, Δ1n sets, Σ1n sets, or Π1n sets. It follows from determinacy of differences of sets in Γ. Since Borel determinacy
Determinacy
In set theory, a branch of mathematics, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.-Games:...
is proved in ZFC, ZFC implies Wadge's lemma for Borel sets.
Structure of the Wadge hierarchy
MartinDonald A. Martin
Donald A. Martin is a set theorist and philosopher of mathematics at UCLA, where he is a member of the faculty of mathematics and philosophy....
and Monk proved in 1973 that AD
Axiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
implies the Wadge order for Baire space is well founded. Hence under AD, the Wadge classes modulo complements form a wellorder. The Wadge rank of a set
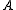is the order type of the set of Wadge degrees modulo complements strictly below [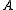]W. The length of the Wadge hierarchy has been shown to be Θ. Wadge also proved that the length of the Wadge hierarchy restricted to the Borel sets is φω1(1) (or φω1(2) depending on the notation), where φγ is the γth Veblen functionVeblen function
In mathematics, the Veblen functions are a hierarchy of normal functions , introduced by Oswald Veblen in...
to the base ω1 (instead of the usual ω).
As for the Wadge lemma, this holds for any pointclass Γ, assuming the axiom of determinacy
Axiom of determinacy
The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
. If we associate with each set
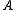the collection of all sets strictly below 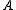on the Wadge hierarchy, this forms a pointclass. Equivalently, for each ordinal α≤θ the collection Wα of sets which show up before stage α is a pointclassPointclass
In the mathematical field of descriptive set theory, a pointclass is a collection of sets of points, where a point is ordinarily understood to be an element of some perfect Polish space. In practice, a pointclass is usually characterized by some sort of definability property; for example, the...
. Conversely, every pointclass is equal to some
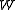α. A pointclass is said to be self-dual if it is closedClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under complementation. It can be shown that Wα is self-dual if and only if α is either 0, an even successor ordinal
Successor ordinal
In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
, or a limit ordinal of countable cofinality
Cofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
.
Other notions of degree
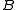Similar notions of reduction and degree arise by replacing the continuous functions by any class of functions F which contains the identity function and is closed under composition. Write ≤F if 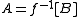for some function 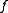in F. Any such class of functions again determines a preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
on the subsets of Baire space. Degrees given by Lipschitz functions are called Lipschitz degrees, and degrees from Borel functions Borel-Wadge degrees.
See also
- Analytical hierarchyAnalytical hierarchyIn mathematical logic and descriptive set theory, the analytical hierarchy is a higher type analogue of the arithmetical hierarchy. It thus continues the classification of sets by the formulas that define them.-The analytical hierarchy of formulas:...
- Arithmetical hierarchyArithmetical hierarchyIn mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
- Axiom of determinacyAxiom of determinacyThe axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...
- Borel hierarchyBorel hierarchyIn mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
- DeterminacyDeterminacyIn set theory, a branch of mathematics, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.-Games:...
- PointclassPointclassIn the mathematical field of descriptive set theory, a pointclass is a collection of sets of points, where a point is ordinarily understood to be an element of some perfect Polish space. In practice, a pointclass is usually characterized by some sort of definability property; for example, the...