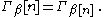Veblen function
Encyclopedia
In mathematics, the Veblen functions are a hierarchy of normal function
s (continuous
strictly increasing function
s from ordinal
s to ordinals), introduced by Oswald Veblen
in . If φ0 is any normal function, then for any non-zero ordinal α, φα is the function enumerating the common fixed point
s of φβ for β<α. These functions are all normal.
this family of functions is known as the Veblen hierarchy.
The function φ1 is the same as the ε function: φ1(α)= εα. If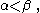 then
then 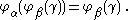 From this and the fact that φβ is strictly increasing we get the ordering:
From this and the fact that φβ is strictly increasing we get the ordering: 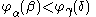 if and only if either (
if and only if either ( and
and 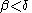 ) or (
) or ( and
and 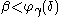 ) or (
) or (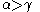 and
and 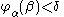 ).
).
ω is a distinguished strictly increasing ω-sequence which has the ordinal as its limit. If one has fundamental sequences for α and all smaller limit ordinals, then one can create an explicit constructive bijection between ω and α, (i.e. one not using the axiom of choice). Here we will describe fundamental sequences for the Veblen hierarchy of ordinals. The image of n under the fundamental sequence for α will be indicated by α[n].
A variation of Cantor normal form used in connection with the Veblen hierarchy is — every nonzero ordinal number α can be uniquely written as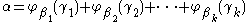 , where k>0 is a natural number and each term after the first is less than or equal to the previous term,
, where k>0 is a natural number and each term after the first is less than or equal to the previous term,  and each
and each 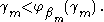 If a fundamental sequence can be provided for the last term, then that term can be replaced by such a sequence to get
If a fundamental sequence can be provided for the last term, then that term can be replaced by such a sequence to get 
For any β, if γ is a limit with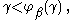 then let
then let 
No such sequence can be provided for = ω0 = 1 because it does not have cofinality ω.
= ω0 = 1 because it does not have cofinality ω.
For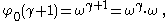 we choose
we choose 
For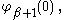 we use
we use  and
and 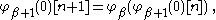 i.e. 0,
i.e. 0, 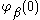 ,
, 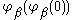 , etc..
, etc..
For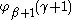 , we use
, we use 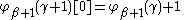 and
and 
Now suppose that β is a limit:
If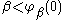 , then let
, then let 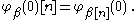
For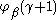 , use
, use 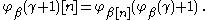
Otherwise, the ordinal cannot be described in terms of smaller ordinals using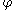 and this scheme does not apply to it.
and this scheme does not apply to it.
Γ0 is the Feferman–Schütte ordinal
, i.e. it is the smallest α such that φα(0) = α.
For Γ0, a fundamental sequence could be chosen to be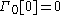 and
and 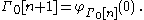
For Γβ+1, let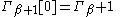 and
and 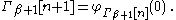
For Γβ where is a limit, let
is a limit, let 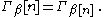
Normal function
In axiomatic set theory, a function f : Ord → Ord is called normal iff it is continuous and strictly monotonically increasing. This is equivalent to the following two conditions:...
s (continuous
Continuous function (set theory)
In mathematics, specifically set theory, a continuous function is a sequence of ordinals such that the values assumed at limit stages are the limits of all values at previous stages...
strictly increasing function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s from ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s to ordinals), introduced by Oswald Veblen
Oswald Veblen
Oswald Veblen was an American mathematician, geometer and topologist, whose work found application in atomic physics and the theory of relativity. He proved the Jordan curve theorem in 1905.-Life:...
in . If φ0 is any normal function, then for any non-zero ordinal α, φα is the function enumerating the common fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of φβ for β<α. These functions are all normal.
The Veblen hierarchy
In the special case when φ0(α)=ωαthis family of functions is known as the Veblen hierarchy.
The function φ1 is the same as the ε function: φ1(α)= εα. If
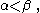 then
then 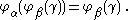 From this and the fact that φβ is strictly increasing we get the ordering:
From this and the fact that φβ is strictly increasing we get the ordering: 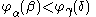 if and only if either (
if and only if either ( and
and 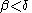 ) or (
) or ( and
and 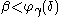 ) or (
) or (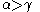 and
and 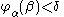 ).
).Fundamental sequences for the Veblen hierarchy
The fundamental sequence for an ordinal with cofinalityCofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
ω is a distinguished strictly increasing ω-sequence which has the ordinal as its limit. If one has fundamental sequences for α and all smaller limit ordinals, then one can create an explicit constructive bijection between ω and α, (i.e. one not using the axiom of choice). Here we will describe fundamental sequences for the Veblen hierarchy of ordinals. The image of n under the fundamental sequence for α will be indicated by α[n].
A variation of Cantor normal form used in connection with the Veblen hierarchy is — every nonzero ordinal number α can be uniquely written as
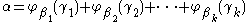 , where k>0 is a natural number and each term after the first is less than or equal to the previous term,
, where k>0 is a natural number and each term after the first is less than or equal to the previous term,  and each
and each 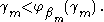 If a fundamental sequence can be provided for the last term, then that term can be replaced by such a sequence to get
If a fundamental sequence can be provided for the last term, then that term can be replaced by such a sequence to get 
For any β, if γ is a limit with
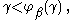 then let
then let 
No such sequence can be provided for
 = ω0 = 1 because it does not have cofinality ω.
= ω0 = 1 because it does not have cofinality ω.For
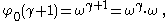 we choose
we choose 
For
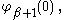 we use
we use  and
and 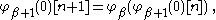 i.e. 0,
i.e. 0, 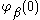 ,
, 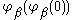 , etc..
, etc..For
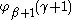 , we use
, we use 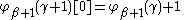 and
and 
Now suppose that β is a limit:
If
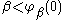 , then let
, then let 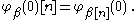
For
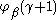 , use
, use 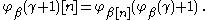
Otherwise, the ordinal cannot be described in terms of smaller ordinals using
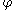 and this scheme does not apply to it.
and this scheme does not apply to it.The Γ function
The function Γ enumerates the ordinals α such that φα(0) = α.Γ0 is the Feferman–Schütte ordinal
Feferman–Schütte ordinal
In mathematics, the Feferman–Schütte ordinal Γ0 is a large countable ordinal.It is the proof theoretic ordinal of several mathematical theories, such as arithmetical transfinite recursion.It is named after Solomon Feferman and Kurt Schütte....
, i.e. it is the smallest α such that φα(0) = α.
For Γ0, a fundamental sequence could be chosen to be
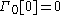 and
and 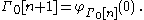
For Γβ+1, let
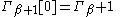 and
and 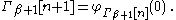
For Γβ where
 is a limit, let
is a limit, let