
Veronese surface
Encyclopedia
In mathematics
, the Veronese surface is an algebraic surface
in five-dimensional projective space
, and is realized by the Veronese embedding, the embedding of the projective plane
given by the complete linear system of conics. It is named after Giuseppe Veronese
(1854–1917). Its generalization to higher dimension is known as the Veronese variety.
The surface admits an embedding in the four-dimensional projective space defined by the projection from a general point in the five-dimensional space. Its general projection to three-dimensional projective space is called a Steiner surface
.

given by
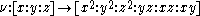
where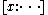 denotes homogeneous coordinates
denotes homogeneous coordinates
. The map is known as the Veronese embedding.
is known as the Veronese embedding.
. A conic is a degree 2 plane curve, thus defined by an equation:
The pairing between coefficients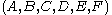 and variables
and variables  is linear in coefficients and quadratic in the variables; the Veronese map makes it linear in the coefficients and linear in the monomials. Thus for a fixed point
is linear in coefficients and quadratic in the variables; the Veronese map makes it linear in the coefficients and linear in the monomials. Thus for a fixed point 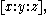 the condition that a conic contains the point is a linear equation in the coefficients, which formalizes the statement that "passing through a point imposes a linear condition on conics". The subtler statement that "five points in general linear position impose independent linear conditions on conics," and thus define a unique conic (as the intersection of five hyperplanes in 5-space is a point) corresponds to the statement that under the Veronese map, points in general position are mapped to points in general position, which corresponds to the fact that the map is biregular (and thus the image of points are in special position if and only if the points were originally in special position).
the condition that a conic contains the point is a linear equation in the coefficients, which formalizes the statement that "passing through a point imposes a linear condition on conics". The subtler statement that "five points in general linear position impose independent linear conditions on conics," and thus define a unique conic (as the intersection of five hyperplanes in 5-space is a point) corresponds to the statement that under the Veronese map, points in general position are mapped to points in general position, which corresponds to the fact that the map is biregular (and thus the image of points are in special position if and only if the points were originally in special position).
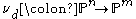
with m given by the multiset coefficient, more familiarly the binomial coefficient
, or more elegantly the rising factorial, as:
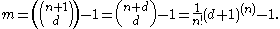
The map sends to all possible monomial
to all possible monomial
s of total degree d, thus the appearance of combinatorial functions; the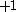 and
and  are due to projectivization. The last expression shows that for fixed source dimension n, the target dimension is a polynomial in d of degree n and leading coefficient
are due to projectivization. The last expression shows that for fixed source dimension n, the target dimension is a polynomial in d of degree n and leading coefficient 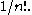
For low degree,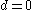 is the trivial constant map to
is the trivial constant map to  and
and  is the identity map on
is the identity map on 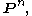 so d is generally taken to be 2 or more.
so d is generally taken to be 2 or more.
One may define the Veronese map in a coordinate-free way, as
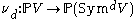
where V is any vector space
of finite dimension, and are its symmetric powers of degree d. This is homogeneous of degree d under scalar multiplication on V, and therefore passes to a mapping on the underlying projective space
are its symmetric powers of degree d. This is homogeneous of degree d under scalar multiplication on V, and therefore passes to a mapping on the underlying projective space
s.
If the vector space V is defined over a field
K which does not have characteristic zero, then the definition must be altered to be understood as a mapping to the dual space of polynomials on V. This is because for fields with finite characteristic p, the pth powers of elements of V are not rational normal curves, but are of course a line. (See, for example additive polynomial
for a treatment of polynomials over a field of finite characteristic).
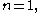 the Veronese variety is known as the rational normal curve, of which the lower-degree examples are familiar.
the Veronese variety is known as the rational normal curve, of which the lower-degree examples are familiar.
; furthermore, these are isomorphic in the sense that the inverse map exists and is regular
– the Veronese map is biregular. More precisely, the images of open set
s in the Zariski topology
are again open.
Biregularity has a number of important consequences. Most significant is that the image of points in general position
under the Veronese map are again in general position
, as if the image satisfies some special condition then this may be pulled back to the original point. This shows that "passing through k points in general position" imposes k independent linear conditions on a variety.
This may be used to show that any projective variety is the intersection of a Veronese variety and a linear space, and thus that any projective variety is isomorphic to an intersection of quadric
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Veronese surface is an algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
in five-dimensional projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, and is realized by the Veronese embedding, the embedding of the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
given by the complete linear system of conics. It is named after Giuseppe Veronese
Giuseppe Veronese
Giuseppe Veronese was an Italian mathematician. He was born in Chioggia, near Venice.Although his work was severely criticised as unsound by Peano, he is now recognised as having priority on many ideas that have since become parts of transfinite numbers and model theory, and as one of the...
(1854–1917). Its generalization to higher dimension is known as the Veronese variety.
The surface admits an embedding in the four-dimensional projective space defined by the projection from a general point in the five-dimensional space. Its general projection to three-dimensional projective space is called a Steiner surface
Steiner surface
In geometry, a branch of mathematics, the Steiner surfaces, discovered by Jakob Steiner, are mappings of the real projective plane into three-dimensional real projective space...
.
Definition
The Veronese surface is a mapping
given by
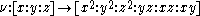
where
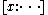 denotes homogeneous coordinates
denotes homogeneous coordinatesHomogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
. The map
 is known as the Veronese embedding.
is known as the Veronese embedding.Motivation
The Veronese surface arises naturally in the study of conics, specifically in formalizing the statement that five points determine a conicFive points determine a conic
In geometry, just as two points determine a line , five points determine a conic . There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.Formally, given any five points in the plane in general...
. A conic is a degree 2 plane curve, thus defined by an equation:

The pairing between coefficients
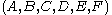 and variables
and variables  is linear in coefficients and quadratic in the variables; the Veronese map makes it linear in the coefficients and linear in the monomials. Thus for a fixed point
is linear in coefficients and quadratic in the variables; the Veronese map makes it linear in the coefficients and linear in the monomials. Thus for a fixed point 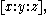 the condition that a conic contains the point is a linear equation in the coefficients, which formalizes the statement that "passing through a point imposes a linear condition on conics". The subtler statement that "five points in general linear position impose independent linear conditions on conics," and thus define a unique conic (as the intersection of five hyperplanes in 5-space is a point) corresponds to the statement that under the Veronese map, points in general position are mapped to points in general position, which corresponds to the fact that the map is biregular (and thus the image of points are in special position if and only if the points were originally in special position).
the condition that a conic contains the point is a linear equation in the coefficients, which formalizes the statement that "passing through a point imposes a linear condition on conics". The subtler statement that "five points in general linear position impose independent linear conditions on conics," and thus define a unique conic (as the intersection of five hyperplanes in 5-space is a point) corresponds to the statement that under the Veronese map, points in general position are mapped to points in general position, which corresponds to the fact that the map is biregular (and thus the image of points are in special position if and only if the points were originally in special position).Veronese map
The Veronese map or Veronese variety generalizes this idea to mappings of general degree d in n+1 variables. That is, the Veronese map of degree d is the map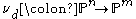
with m given by the multiset coefficient, more familiarly the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
, or more elegantly the rising factorial, as:
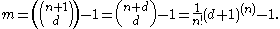
The map sends
 to all possible monomial
to all possible monomialMonomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s of total degree d, thus the appearance of combinatorial functions; the
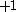 and
and  are due to projectivization. The last expression shows that for fixed source dimension n, the target dimension is a polynomial in d of degree n and leading coefficient
are due to projectivization. The last expression shows that for fixed source dimension n, the target dimension is a polynomial in d of degree n and leading coefficient 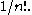
For low degree,
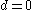 is the trivial constant map to
is the trivial constant map to  and
and  is the identity map on
is the identity map on 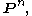 so d is generally taken to be 2 or more.
so d is generally taken to be 2 or more.One may define the Veronese map in a coordinate-free way, as
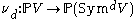
where V is any vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of finite dimension, and
 are its symmetric powers of degree d. This is homogeneous of degree d under scalar multiplication on V, and therefore passes to a mapping on the underlying projective space
are its symmetric powers of degree d. This is homogeneous of degree d under scalar multiplication on V, and therefore passes to a mapping on the underlying projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
s.
If the vector space V is defined over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K which does not have characteristic zero, then the definition must be altered to be understood as a mapping to the dual space of polynomials on V. This is because for fields with finite characteristic p, the pth powers of elements of V are not rational normal curves, but are of course a line. (See, for example additive polynomial
Additive polynomial
In mathematics, the additive polynomials are an important topic in classical algebraic number theory.-Definition:Let k be a field of characteristic p, with p a prime number. A polynomial P with coefficients in k is called an additive polynomial, or a Frobenius polynomial, ifP=P+P\,as polynomials...
for a treatment of polynomials over a field of finite characteristic).
Rational normal curve
For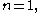 the Veronese variety is known as the rational normal curve, of which the lower-degree examples are familiar.
the Veronese variety is known as the rational normal curve, of which the lower-degree examples are familiar.
- For
 the Veronese map is simply the identity map on the projective line.
the Veronese map is simply the identity map on the projective line. - For
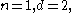 the Veronese variety is the standard parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
the Veronese variety is the standard parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
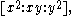 in affine coordinates
in affine coordinates 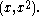
- For
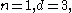 the Veronese variety is the twisted cubicTwisted cubicIn mathematics, a twisted cubic is a smooth, rational curve C of degree three in projective 3-space P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation...
the Veronese variety is the twisted cubicTwisted cubicIn mathematics, a twisted cubic is a smooth, rational curve C of degree three in projective 3-space P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation...
,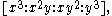 in affine coordinates
in affine coordinates 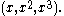
Biregular
The image of a variety under the Veronese map is again a variety, rather than simply a constructible setConstructible set (topology)
In topology, a constructible set in a noetherian topological space is a finite union of locally closed sets. Constructible sets form a Boolean algebra In fact, the constructible sets are precisely the...
; furthermore, these are isomorphic in the sense that the inverse map exists and is regular
Regular function
In mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
– the Veronese map is biregular. More precisely, the images of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s in the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
are again open.
Biregularity has a number of important consequences. Most significant is that the image of points in general position
General position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
under the Veronese map are again in general position
General position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
, as if the image satisfies some special condition then this may be pulled back to the original point. This shows that "passing through k points in general position" imposes k independent linear conditions on a variety.
This may be used to show that any projective variety is the intersection of a Veronese variety and a linear space, and thus that any projective variety is isomorphic to an intersection of quadric
Quadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
s.

