
Rational normal curve
Encyclopedia
In mathematics
, the rational normal curve is a smooth, rational curve of degree
of degree
n in projective n-space
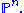 It is a simple example of a projective variety; formally, it is the Veronese variety when the domain is the projective line. For n=2 it is the standard parabola
It is a simple example of a projective variety; formally, it is the Veronese variety when the domain is the projective line. For n=2 it is the standard parabola
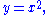 and for n=3 it is the twisted cubic
and for n=3 it is the twisted cubic
.
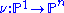
which assigns to the homogeneous coordinates
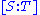 the value
the value

In the affine coordinates of the chart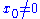 the map is simply
the map is simply
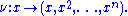
That is, the rational normal curve is the closure by a single point at infinity of the affine curve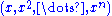 .
.
Equivalently, rational normal curve may be understood to be a projective variety, defined as the common zero locus of the homogeneous polynomial
s
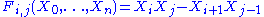
where are the homogeneous coordinates on
are the homogeneous coordinates on 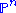 . The full set of these polynomials is not needed; it is sufficient to pick n of these to specify the curve.
. The full set of these polynomials is not needed; it is sufficient to pick n of these to specify the curve.
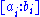 be
be  distinct points in
distinct points in 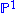 . Then the polynomial
. Then the polynomial
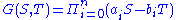
is a homogeneous polynomial
of degree with distinct roots. The polynomials
with distinct roots. The polynomials
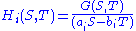
are then a basis
for the space of homogeneous polynomials of degree n. The map
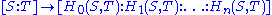
or, equivalently, dividing by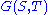
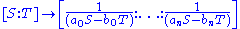
is a rational normal curve. That this is a rational normal curve may be understood by noting that the monomial
s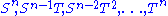 are just one possible basis
are just one possible basis
for the space of degree-n homogeneous polynomials. In fact, any basis
will do. This is just an application of the statement that any two projective varieties are projectively equivalent if they are congruent
modulo the projective linear group
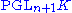 (with K the field
(with K the field
over which the projective space is defined).
This rational curve sends the zeros of G to each of the coordinate points of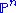 ; that is, all but one of the
; that is, all but one of the 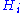 vanish for a zero of G. Conversely, any rational normal curve passing through the n+1 coordinate points may be written parametrically in this way.
vanish for a zero of G. Conversely, any rational normal curve passing through the n+1 coordinate points may be written parametrically in this way.
There are independent quadric
independent quadric
s that generate the ideal
of the curve.
The curve is not a complete intersection
, for . This means it is not defined by the number of equations equal to its codimension
. This means it is not defined by the number of equations equal to its codimension
 .
.
The canonical mapping for a hyperelliptic curve has image a rational normal curve, and is 2-to-1.
Every irreducible non-degenerate curve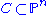 of degree
of degree  is a rational normal curve.
is a rational normal curve.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the rational normal curve is a smooth, rational curve
 of degree
of degreeDegree of an algebraic variety
The degree of an algebraic variety in mathematics is defined, for a projective variety V, by an elementary use of intersection theory.For V embedded in a projective space Pn and defined over some algebraically closed field K, the degree d of V is the number of points of intersection of V, defined...
n in projective n-space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
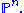 It is a simple example of a projective variety; formally, it is the Veronese variety when the domain is the projective line. For n=2 it is the standard parabola
It is a simple example of a projective variety; formally, it is the Veronese variety when the domain is the projective line. For n=2 it is the standard parabolaParabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
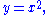 and for n=3 it is the twisted cubic
and for n=3 it is the twisted cubicTwisted cubic
In mathematics, a twisted cubic is a smooth, rational curve C of degree three in projective 3-space P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation...
.
Definition
The rational normal curve may be given parametrically as the image of the map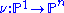
which assigns to the homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
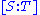 the value
the value
In the affine coordinates of the chart
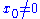 the map is simply
the map is simply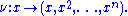
That is, the rational normal curve is the closure by a single point at infinity of the affine curve
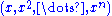 .
.Equivalently, rational normal curve may be understood to be a projective variety, defined as the common zero locus of the homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s
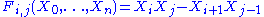
where
 are the homogeneous coordinates on
are the homogeneous coordinates on 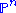 . The full set of these polynomials is not needed; it is sufficient to pick n of these to specify the curve.
. The full set of these polynomials is not needed; it is sufficient to pick n of these to specify the curve.Alternate parameterization
Let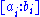 be
be  distinct points in
distinct points in 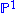 . Then the polynomial
. Then the polynomial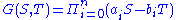
is a homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
of degree
 with distinct roots. The polynomials
with distinct roots. The polynomials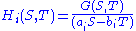
are then a basis
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for the space of homogeneous polynomials of degree n. The map
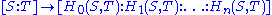
or, equivalently, dividing by
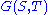
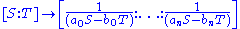
is a rational normal curve. That this is a rational normal curve may be understood by noting that the monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s
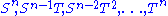 are just one possible basis
are just one possible basisBase (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for the space of degree-n homogeneous polynomials. In fact, any basis
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
will do. This is just an application of the statement that any two projective varieties are projectively equivalent if they are congruent
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
modulo the projective linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
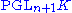 (with K the field
(with K the fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
over which the projective space is defined).
This rational curve sends the zeros of G to each of the coordinate points of
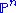 ; that is, all but one of the
; that is, all but one of the 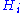 vanish for a zero of G. Conversely, any rational normal curve passing through the n+1 coordinate points may be written parametrically in this way.
vanish for a zero of G. Conversely, any rational normal curve passing through the n+1 coordinate points may be written parametrically in this way.Properties
The rational normal curve has an assortment of nice properties:- Any
 points on
points on  are linearly independent, and span
are linearly independent, and span  . This property distinguishes the rational normal curve from all other curves.
. This property distinguishes the rational normal curve from all other curves. - Given
 points in
points in  in linear general positionGeneral positionIn algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
in linear general positionGeneral positionIn algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
(that is, with no lying in a hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
lying in a hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
), there is a unique rational normal curve passing through them. The curve may be explicitly specified using the parametric representation, by arranging of the points to lie on the coordinate axes, and then mapping the other two points to
of the points to lie on the coordinate axes, and then mapping the other two points to 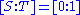 and
and 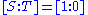 .
. - The tangent and secant lines of a rational normal curve are pairwise disjoint, except at points of the curve itself. This is a property shared by sufficiently positive embeddings of any projective variety.
There are
 independent quadric
independent quadricQuadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
s that generate the ideal
Ideal
-In philosophy:* Ideal , values that one actively pursues as goals* Platonic ideal, a philosophical idea of trueness of form, associated with Plato-In mathematics:* Ideal , special subsets of a ring considered in abstract algebra...
of the curve.
The curve is not a complete intersection
Complete intersection
In mathematics, an algebraic variety V in projective space is a complete intersection if it can be defined by the vanishing of the number of homogeneous polynomials indicated by its codimension...
, for
 . This means it is not defined by the number of equations equal to its codimension
. This means it is not defined by the number of equations equal to its codimensionCodimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
 .
.The canonical mapping for a hyperelliptic curve has image a rational normal curve, and is 2-to-1.
Every irreducible non-degenerate curve
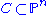 of degree
of degree  is a rational normal curve.
is a rational normal curve.

