Additive polynomial
Encyclopedia
In mathematics
, the additive polynomials are an important topic in classical algebraic number theory
.
of characteristic
p, with p a prime number
. A polynomial
P(x) with coefficients in k is called an additive polynomial, or a Frobenius polynomial, if
as polynomials in a and b. It is equivalent to assume that this equality holds for all a and b in some infinite field containing k, such as its algebraic closure.
Occasionally absolutely additive is used for the condition above, and additive is used for the weaker condition that P(a + b) = P(a) + P(b) for all a and b in the field. For infinite fields the conditions are equivalent, but for finite fields they are not, and the weaker condition is the "wrong" one and does not behave well. For example, over a field of order q any multiple P of xq − x will satisfy P(a + b) = P(a) + P(b) for all a and b in the field, but will usually not be (absolutely) additive.
Since p is prime, for all n = 1, ..., p−1 the binomial coefficient
is divisible by p, which implies that
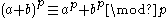
as polynomials in a and b.
Similarly all the polynomials of the form
are additive, where n is a non-negative integer.
of polynomials
with coefficients in k is also an additive polynomial. An interesting question is whether there are other additive polynomials except these linear combinations. The answer is that these are the only ones.
One can check that if P(x) and M(x) are additive polynomials, then so are P(x) + M(x) and P(M(x)). These imply that the additive polynomials form a ring
under polynomial addition and composition. This ring is denoted
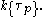
This ring is not commutative unless k equals the field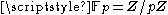
(see modular arithmetic
). Indeed, consider the additive polynomials ax and xp for a coefficient a in k. For them to commute under composition, we must have
or ap − a = 0. This is false for a not a root of this equation, that is, for a outside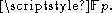
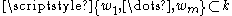be the set of its roots. Assuming that the roots of P(x) are distinct (that is, P(x) is separable
), then P(x) is additive if and only if the set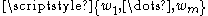
forms a group
with the field addition.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the additive polynomials are an important topic in classical algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
.
Definition
Let k be a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
p, with p a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. A polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
P(x) with coefficients in k is called an additive polynomial, or a Frobenius polynomial, if
as polynomials in a and b. It is equivalent to assume that this equality holds for all a and b in some infinite field containing k, such as its algebraic closure.
Occasionally absolutely additive is used for the condition above, and additive is used for the weaker condition that P(a + b) = P(a) + P(b) for all a and b in the field. For infinite fields the conditions are equivalent, but for finite fields they are not, and the weaker condition is the "wrong" one and does not behave well. For example, over a field of order q any multiple P of xq − x will satisfy P(a + b) = P(a) + P(b) for all a and b in the field, but will usually not be (absolutely) additive.
Examples
The polynomial xp is additive. Indeed, for any a and b in the algebraic closure of k one has by the binomial theoremBinomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
Since p is prime, for all n = 1, ..., p−1 the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
is divisible by p, which implies that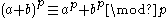as polynomials in a and b.
Similarly all the polynomials of the form
are additive, where n is a non-negative integer.
The ring of additive polynomials
It is quite easy to prove that any linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of polynomials
with coefficients in k is also an additive polynomial. An interesting question is whether there are other additive polynomials except these linear combinations. The answer is that these are the only ones.One can check that if P(x) and M(x) are additive polynomials, then so are P(x) + M(x) and P(M(x)). These imply that the additive polynomials form a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
under polynomial addition and composition. This ring is denoted
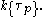
This ring is not commutative unless k equals the field
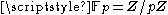(see modular arithmeticModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
). Indeed, consider the additive polynomials ax and xp for a coefficient a in k. For them to commute under composition, we must have
or ap − a = 0. This is false for a not a root of this equation, that is, for a outside
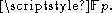
The fundamental theorem of additive polynomials
Let P(x) be a polynomial with coefficients in k, and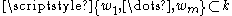 be the set of its roots. Assuming that the roots of P(x) are distinct (that is, P(x) is separableSeparable polynomial
In mathematics, two slightly different notions of separable polynomial are used, by different authors.According to the most common one, a polynomial P over a given field K is separable if all its roots are distinct in an algebraic closure of K, that is the number of its distinct roots is equal to...
), then P(x) is additive if and only if the set
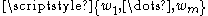forms a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
with the field addition.