Mixed tensor
Encyclopedia
In tensor analysis, a mixed tensor is a tensor
which is neither strictly covariant nor strictly contravariant; at least one of the indices of a mixed tensor will be a subscript (covariant) and at least one of the indices will be a superscript (contravariant).
A mixed tensor of type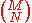
, also written "type (M, N)", with both M > 0 and N > 0, is a tensor which has M contravariant indices and N covariant indices. Such tensor can be defined as a linear function which maps an M+N-tuple of M one-form
s and N vectors to a scalar
.
.
The first one is covariant, the last one contravariant, and the remaining ones mixed. Notationally, these tensors differ from each other by the covariance/contravariance of their indices. A given contravariant index of a tensor can be lowered using the metric tensor
gμν, and a given covariant index can be raised using the inverse metric tensor gμν. Thus, gμν could be called the index lowering operator and gμν the index raising operator.
Generally, the covariant metric tensor, contracted with a tensor of type (M,N), yields a tensor of type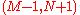
, whereas its contravariant inverse, contracted with a tensor of type 
, yields a tensor of type 
.
,
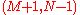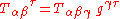where
is the same tensor as 
, because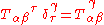
,
with Kronecker δ acting here like an identity matrix.
Likewise,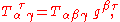
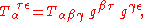
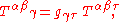
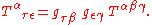
Raising an index of the metric tensor is equivalent to contracting it with its inverse, yielding the Kronecker delta,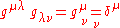
,
so any mixed version of the metric tensor will be equal to the Kronecker delta, which will also be mixed.
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
which is neither strictly covariant nor strictly contravariant; at least one of the indices of a mixed tensor will be a subscript (covariant) and at least one of the indices will be a superscript (contravariant).
A mixed tensor of type
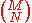, also written "type (M, N)", with both M > 0 and N > 0, is a tensor which has M contravariant indices and N covariant indices. Such tensor can be defined as a linear function which maps an M+N-tuple of M one-formOne-form
In linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...
s and N vectors to a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
.
Index raising and lowering
Consider the following octet of related tensors:.The first one is covariant, the last one contravariant, and the remaining ones mixed. Notationally, these tensors differ from each other by the covariance/contravariance of their indices. A given contravariant index of a tensor can be lowered using the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
gμν, and a given covariant index can be raised using the inverse metric tensor gμν. Thus, gμν could be called the index lowering operator and gμν the index raising operator.
Generally, the covariant metric tensor, contracted with a tensor of type (M,N), yields a tensor of type
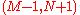, whereas its contravariant inverse, contracted with a tensor of type , yields a tensor of type 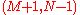.Examples
As an example, a mixed tensor of type (1, 2) can be obtained by raising an index of a covariant tensor of type (0, 3),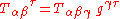,where
is the same tensor as , because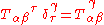,with Kronecker δ acting here like an identity matrix.
Likewise,
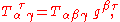
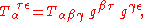
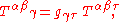
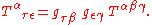
Raising an index of the metric tensor is equivalent to contracting it with its inverse, yielding the Kronecker delta,
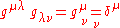,so any mixed version of the metric tensor will be equal to the Kronecker delta, which will also be mixed.
See also
- Covariance and contravariance of vectors
- Tensor (intrinsic definition)Tensor (intrinsic definition)In mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multi-linear concept...
- Two-point tensorTwo-point tensorTwo-point tensors, or double vectors, are tensor-like quantities which transform as vectors with respect to each of their indices and are used in continuum mechanics to transform between reference and present coordinates...