
Tait conjectures
Encyclopedia
The Tait conjectures are conjectures made by Peter Guthrie Tait
in his study of knots
. The Tait conjectures involve concepts in knot theory
such as alternating knot
s, chirality, and writhe
. All of the Tait conjectures have been solved, the most recent being the Tait flyping conjecture proven in 1991 by Morwen Thistlethwaite
and William Menasco
.
 Tait came up with his conjectures after his attempt to tabulate
Tait came up with his conjectures after his attempt to tabulate
all knots in the late 19th century. As a founder of the field of knot theory
, his work lacks a mathematically rigorous framework, and it is unclear whether the conjectures apply to all knots, or just to alternating knot
s. Most of them are only true for alternating knot
s. In the Tait conjectures, a knot diagram is reduced if all the isthmi have been removed.
was a knot invariant
, specifically:
In other words, the crossing number of a reduced, alternating link is an invariant
of the knot. This conjecture was proven by Morwen Thistlethwaite
, Louis Kauffman
and K. Murasugi in 1987, using the Jones polynomial.
Another one of his conjectures:
This conjecture was also proven by Morwen Thistlethwaite
.
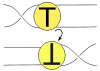 The Tait flyping conjecture can be stated:
The Tait flyping conjecture can be stated:
The Tait flyping conjecture was proven by Morwen Thistlethwaite
and William Menasco
in 1991.
The Tait flyping conjecture implies some more of Tait's conjectures:
This follows because flyping
preserves writhe
. This was proven earlier by Morwen Thistlethwaite
, Louis Kauffman
and K. Murasugi in 1987.
For non-alternating knots this conjecture is not true, assuming so lead to the duplication of the Perko pair
, because it has two reduced projections with different writhe
.
The flyping conjecture also implies this conjecture:
This follows because a knot's mirror image has opposite writhe
.
This one is also only true for alternating knots, a non-alternating amphichiral
knot with crossing number 15 was found, by Morwen Thistlethwaite
.
Peter Guthrie Tait
Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
in his study of knots
History of knot theory
For thousands of years, knots have been used for basic purposes such as recording information, fastening and tying objects together. Over time people realized that different knots were better at different tasks, such as climbing or sailing. Knots were also regarded as having spiritual and...
. The Tait conjectures involve concepts in knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
such as alternating knot
Alternating knot
In knot theory, a link diagram is alternating if the crossings alternate under, over, under, over, as you travel along each component of the link. A link is alternating if it has an alternating diagram....
s, chirality, and writhe
Writhe
In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
. All of the Tait conjectures have been solved, the most recent being the Tait flyping conjecture proven in 1991 by Morwen Thistlethwaite
Morwen Thistlethwaite
Morwen B. Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory, and Rubik's cube group theory.-Biography:...
and William Menasco
William Menasco
William W. Menasco is a topologist and a professor at the University at Buffalo. He is best known for his work in knot theory.-Biography:Menasco received is B.A. from the University of California, Los Angeles in 1975, and his Ph.D. from the University of California, Berkeley in 1981, where his...
.
Background

Knot tabulation
Ever since Sir William Thomson's vortex theory, mathematicians have tried to classify and tabulate all possible knots. As of May 2008 all prime knots up to 16 crossings have been tabulated.-Beginnings:...
all knots in the late 19th century. As a founder of the field of knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, his work lacks a mathematically rigorous framework, and it is unclear whether the conjectures apply to all knots, or just to alternating knot
Alternating knot
In knot theory, a link diagram is alternating if the crossings alternate under, over, under, over, as you travel along each component of the link. A link is alternating if it has an alternating diagram....
s. Most of them are only true for alternating knot
Alternating knot
In knot theory, a link diagram is alternating if the crossings alternate under, over, under, over, as you travel along each component of the link. A link is alternating if it has an alternating diagram....
s. In the Tait conjectures, a knot diagram is reduced if all the isthmi have been removed.
The Tait conjectures
Tait conjectured that in certain circumstances, crossing numberCrossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
was a knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
, specifically:
Any reduced diagram of an alternating link has the fewest possible crossingsCrossing number (knot theory)In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
.
In other words, the crossing number of a reduced, alternating link is an invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
of the knot. This conjecture was proven by Morwen Thistlethwaite
Morwen Thistlethwaite
Morwen B. Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory, and Rubik's cube group theory.-Biography:...
, Louis Kauffman
Louis Kauffman
Louis H. Kauffman is an American mathematician, topologist, and professor of Mathematics in the Department of Mathematics, Statistics, and Computer science at the University of Illinois at Chicago...
and K. Murasugi in 1987, using the Jones polynomial.
Another one of his conjectures:
A reduced alternating link with zero writheWritheIn knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
is achiralAmphichiral knotIn the mathematical field of knot theory, a chiral knot is a knot that is not equivalent to its mirror image. An oriented knot that is equivalent to its mirror image is an amphichiral knot, also called an achiral knot or amphicheiral knot. The chirality of a knot is a knot invariant...
.
This conjecture was also proven by Morwen Thistlethwaite
Morwen Thistlethwaite
Morwen B. Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory, and Rubik's cube group theory.-Biography:...
.
The Tait flyping conjecture

Given any two reduced alternating diagrams D1 and D2 of an oriented, prime alternating link: D1 may be transformed to D2 by means of a sequence of certain simple moves called flypeFlypeIn the mathematical theory of knots, a flype is a kind of manipulation of knot and link diagramsused in the Tait flyping conjecture.It consists of twisting a part of a knot, a tangle: T by 180 degrees. Flype comes from an old Scottish word meaning to fold or to turn back. Two reduced alternating...
s. Also known as the Tait flyping conjecture.
The Tait flyping conjecture was proven by Morwen Thistlethwaite
Morwen Thistlethwaite
Morwen B. Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory, and Rubik's cube group theory.-Biography:...
and William Menasco
William Menasco
William W. Menasco is a topologist and a professor at the University at Buffalo. He is best known for his work in knot theory.-Biography:Menasco received is B.A. from the University of California, Los Angeles in 1975, and his Ph.D. from the University of California, Berkeley in 1981, where his...
in 1991.
The Tait flyping conjecture implies some more of Tait's conjectures:
Any two reduced diagrams of the same alternating knotKnot (mathematics)In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
have the same writheWritheIn knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
.
This follows because flyping
Flype
In the mathematical theory of knots, a flype is a kind of manipulation of knot and link diagramsused in the Tait flyping conjecture.It consists of twisting a part of a knot, a tangle: T by 180 degrees. Flype comes from an old Scottish word meaning to fold or to turn back. Two reduced alternating...
preserves writhe
Writhe
In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
. This was proven earlier by Morwen Thistlethwaite
Morwen Thistlethwaite
Morwen B. Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory, and Rubik's cube group theory.-Biography:...
, Louis Kauffman
Louis Kauffman
Louis H. Kauffman is an American mathematician, topologist, and professor of Mathematics in the Department of Mathematics, Statistics, and Computer science at the University of Illinois at Chicago...
and K. Murasugi in 1987.
For non-alternating knots this conjecture is not true, assuming so lead to the duplication of the Perko pair
Perko pair
In the mathematical theory of knots, the Perko pair, named after Kenneth Perko, is a pair of entries in classical knot tables that actually represent the same knot. In Rolfsen's knot table, this supposed pair of distinct knots is labeled 10161 and 10162...
, because it has two reduced projections with different writhe
Writhe
In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
.
The flyping conjecture also implies this conjecture:
Alternating amphicheiral knots have even crossing numberCrossing number (knot theory)In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
.
This follows because a knot's mirror image has opposite writhe
Writhe
In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
.
This one is also only true for alternating knots, a non-alternating amphichiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
knot with crossing number 15 was found, by Morwen Thistlethwaite
Morwen Thistlethwaite
Morwen B. Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory, and Rubik's cube group theory.-Biography:...
.

