Ever since Sir William Thomson's vortex theory

Vortex theory

Vortex theory may refer to:*Mechanical explanations of gravitation — a theory to explain gravitation.*History of knot theory — a theory to explain the atom....

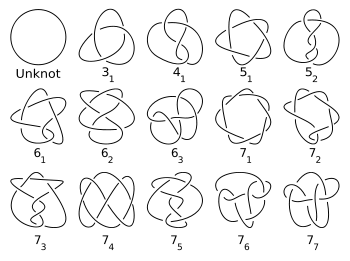
, mathematicians have tried to classify and tabulate all possible knots

Knot (mathematics)

In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...

. As of May 2008 all prime knot

Prime knot

In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...

s up to 16 crossings

Crossing number (knot theory)

In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....

 have been tabulated.

Beginnings

In an attempt to make a periodic table of the elements, P. G. Tait, C. N. Little and others started counting all possible knots.

Perko pair

In 1974 Perko discovered a duplication in the Tait-Little tables, called the Perko pair

Perko pair

In the mathematical theory of knots, the Perko pair, named after Kenneth Perko, is a pair of entries in classical knot tables that actually represent the same knot. In Rolfsen's knot table, this supposed pair of distinct knots is labeled 10161 and 10162...

.

New methods

Hoste et al. and Thistlethwaite

Morwen Thistlethwaite

Morwen B. Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory, and Rubik's cube group theory.-Biography:...

 each independently counted all knots with 16 crossings, and both got the same number.

See also

• Knot theory
  Knot theory
  In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
  
  
• Knot (mathematics)
  Knot (mathematics)
  In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
  
  
• History of knot theory
  History of knot theory
  For thousands of years, knots have been used for basic purposes such as recording information, fastening and tying objects together. Over time people realized that different knots were better at different tasks, such as climbing or sailing. Knots were also regarded as having spiritual and...