A line group is a mathematical way of describing symmetries

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

 associated with moving along a line. These symmetries include repeating along that line, making that line a one-dimensional lattice. However, line groups may have more than one dimension, and they may involve those dimensions in its isometries

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

 or symmetry transformations.

One constructs a line group by taking a point group

Point group

In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...

 in the full dimensions of the space, and then adding translations or offsets along the line to each of the point group's elements, in the fashion of constructing a space group

Space group

In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...

. These offsets include the repeats, and a fraction of the repeat, one fraction for each element. For convenience, the fractions are scaled to the size of the repeat; they are thus within the line's unit cell segment.

One-dimensional

There are 2 one-dimensional line groups. They are the infinite limits of the discrete two-dimensional point groups

Point groups in two dimensions

In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O, including O itself...

 C_n and D_n:

Notations				Description	Example
Intl	Orbifold	Coxeter Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M...	P.G.
p1	∞∞	[∞]+	C∞	Translations. Abstract group Z, the integers under addition	... --> --> --> --> ...
p1m	*∞∞	[∞]	D∞	Reflections. Abstract group Dih∞, the infinite dihedral group Infinite dihedral group In mathematics, the infinite dihedral group Dih∞ is an infinite group with properties analogous to those of the finite dihedral groups.-Definition:...	... --> <-- --> <-- ...

Two-dimensional

There are 7 frieze groups

Frieze group

A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

, which involve reflections along the line, reflections perpendicular to the line, and 180° rotations in the two dimensions.

7 frieze group notations and diagram

IUC	Orbifold	Schönflies Schoenflies notation The Schoenflies notation or Schönflies notation, named after the German mathematician Arthur Moritz Schoenflies, is one of two conventions commonly used to describe Point groups. This notation is used in spectroscopy. The other convention is the Hermann–Mauguin notation, also known as the...	Conway John Horton Conway John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...	Coxeter Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M...	Fundamental domain
p1	∞∞	C∞	C∞	[∞,1]+
p1m1	*∞∞	C∞v	CD2∞	[∞,1]
p11g	∞x	S2∞	CC2∞	[∞+,2+]
p11m	∞*	C∞h	±C∞	[∞+,2]
p2	22∞	D∞	D2∞	[∞,2]+
p2mg	2*∞	D∞d	DD4∞	[∞,2+]
p2mm	*22∞	D∞h	±D2∞	[∞,2]

Three-dimensional

There are 13 infinite families of three-dimensional line groups, derived from the 7 infinite families of axial three-dimensional point groups

Point groups in three dimensions

In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...

. As with space groups in general, line groups with the same point group can have different patterns of offsets. Each of the families is based on a group of rotations around the axis with order n. The groups are listed in Hermann-Mauguin notation

Hermann-Mauguin notation

Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin...

, and for the point groups, Schönflies notation. There appears to be no comparable notation for the line groups. These groups can also be interpreted as patterns of wallpaper group

Wallpaper group

A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

s wrapped around a cylinder n times and infinitely repeating along the cylinder's axis, much like the three-dimensional point groups and the frieze groups. A table of these groups:

Point group			Line group
Hermann-Mauguin		Schönflies	Hermann-Mauguin		Offset type	Wallpaper			Coxeter Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M... [∞h,2,pv]
Even n	Odd n		Even n	Odd n		IUC	Orbifold Orbifold In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...	Diagram
n		Cn	Pnq		Helical: q	p1	o		[∞+,2,n+]
		S2n	P	P	None	p11g, pg(h)	xx		[(∞,2)+,2n+]
n/m		Cnh	Pn/m	P	None	p11m, pm(h)	**		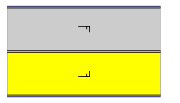[∞+,2,n]
2n/m		C2nh	P2nn/m		Zigzag	c11m, cm(h)	*x		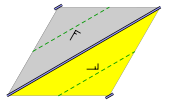[∞+,2+,2n]
nmm	nm	Cnv	Pnmm	Pnm	None	p1m1, pm(v)	**		[∞,2,n+]
			Pncc	Pnc	Planar reflection	p1g1, pg(v)	xx		[∞+,(2,n)+]
2nmm		C2nv	P2nnmc		Zigzag	c1m1, cm(v)	*x		[∞,2+,2n+]
n22	n2	Dn	Pnq22	Pnq2	Helical: q	p2	2222		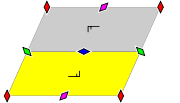[∞,2,n]+
2m	m	Dnd	P2m	Pm	None	p2mg, pmg(h)	22*		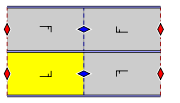[(∞,2)+,2n]
			P2c	Pc	Planar reflection	p2gg, pgg	22x		[∞+,2+,2n+]
n/mmm	2m	Dnh	Pn/mmm	P2m	None	p2mm, pmm	*2222		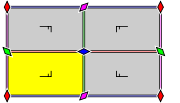[∞,2,n]
			Pn/mcc	P2c	Planar reflection	p2mg, pmg(v)	22*		[∞,(2,n)+]
2n/mmm		D2nh	P2nn/mcm		Zigzag	c2mm, cmm	2*22		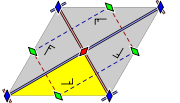[∞,2+,2n]

The offset types are:

• No offset.
• Helical offset with helicity q. For C_n(q) and D_n(q), axial rotation k out of n has an offset (q/n)k mod 1. A particle subjected to the rotations in sequence will thus trace out a helix. D_n(q) includes 180° rotations on axes in the perpendicular plane; those axes have the same helical pattern of offsets relative to their directions.
• Zigzag offset. Helical offset for helicity q = n for total number 2n. Axial rotation k out of 2n has 1/2 if odd, 0 if even, and likewise for the other elements.
• Planar-reflection offset. Every element that is a reflection along a direction in the perpendicular plane has an offset of 1/2. This is analogous to what happens in frieze groups p11g and p2mg.

Note that the wallpaper groups pm, pg, cm, and pmg appear twice. Each appearance has a different orientation relative to the line-group axis; reflection parallel (h) or perpendicular (v). The other groups have no such orientation: p1, p2, pmm, pgg, cmm.

If the point group is constrained to be a crystallographic point group

Crystallographic point group

In crystallography, a crystallographic point group is a set of symmetry operations, like rotations or reflections, that leave a central point fixed while moving other directions and faces of the crystal to the positions of features of the same kind...

, a symmetry of some three-dimensional lattice, then the resulting line group is called a rod group

Rod group

In mathematics, a rod group is a three-dimensional line group whose point group is one of the axial crystallographic point groups. This constraint means that the point group must be the symmetry of some three-dimensional lattice....

. There are 75 rod groups.

• The Coxeter notation
  Coxeter notation
  In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M...
  
   is based on the rectangular wallpaper groups, with the vertical axis wrapped into a cylinder of symmetry order n or 2n.

Going to the continuum limit, with n to ∞, the possible point groups become C_∞, C_∞h, C_∞v, D_∞, and D_∞h, and the line groups have the appropriate possible offsets, with the exception of zigzag.

Helical symmetry

The groups C_n(q) and D_n(q) express the symmetries of helical objects. C_n(q) is for |q| helices oriented in the same direction, while D_n(q) is for |q| unoriented helices and 2|q|, helices with alternating orientations. Reversing the sign of q creates a mirror image, reversing the helices' chirality or handedness. The helices may have their own internal repeat lengths; n becomes the number of turns necessary to produce an integer number of internal repeats. But if the helix's coiling and internal repeating are incommensurable (ratio not a rational number), then n is effectively ∞.

Nucleic acid

Nucleic acid

Nucleic acids are biological molecules essential for life, and include DNA and RNA . Together with proteins, nucleic acids make up the most important macromolecules; each is found in abundance in all living things, where they function in encoding, transmitting and expressing genetic information...

s, DNA

DNA

Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...

 and RNA

RNA

Ribonucleic acid , or RNA, is one of the three major macromolecules that are essential for all known forms of life....

, are well-known for their helical symmetry. Nucleic acids have a well-defined direction, giving single strands C_n(1). Double strands have opposite directions and are on opposite sides of the helix axis, giving them D_n(1).

See also

• Point group
  Point group
  In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
  
  
• Space group
  Space group
  In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
  
  
• One-dimensional symmetry group
• Frieze group
  Frieze group
  A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
  
  
• Rod group
  Rod group
  In mathematics, a rod group is a three-dimensional line group whose point group is one of the axial crystallographic point groups. This constraint means that the point group must be the symmetry of some three-dimensional lattice....