
Compactification (physics)
Encyclopedia
In physics
, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic.
Compactification plays an important part in thermal field theory where one compactifies time, in string theory
where one compactifies the extra dimensions of the theory, and in two- or one-dimensional solid state physics, where one considers a system which is limited in one of the three usual spatial dimensions.
At the limit where the size of the compact dimension goes to zero, no fields depend on this extra dimension, and the theory is dimensionally reduced
.
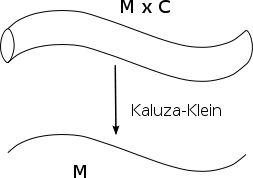
. It tries to conciliate the gap between the conception of our universe based on its four observable dimensions with the ten, eleven, or twenty-six dimensions theoretical equations lead to suppose the universe is made with. For this purpose it is assumed the extra dimensions are "wrapped" up on themselves, or "curled" up on Calabi–Yau spaces, or on orbifold
s. Models in which the compact directions support flux
es are known as flux compactifications. The coupling constant
of string theory
, which determines the probability of strings to split and reconnect, can be described by a field
called dilaton
. This in turn can be described as the size of an extra (eleventh) dimension which is compact. In this way, the ten-dimensional type IIA string theory can be described as the compactification of M-theory
in eleven dimensions. Furthermore, different versions of string theory are related by different compactifications in a procedure known as T-duality
.
The formulation of more precise versions of the meaning of compactification in this context has been promoted by discoveries such as the mysterious duality.
is a Calabi–Yau manifold or generalized Calabi–Yau manifold which is equipped with non-zero values of fluxes, i.e. differential form
s that generalize the concept of an electromagnetic field
(see p-form electrodynamics).
The hypothetical concept of the anthropic landscape in string theory follows from a large number of possibilities in which the integers that characterize the fluxes can be chosen without violating rules of string theory. The flux compactifications can be described as F-theory
vacua or type IIB string theory vacua with or without D-brane
s.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic.
Compactification plays an important part in thermal field theory where one compactifies time, in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
where one compactifies the extra dimensions of the theory, and in two- or one-dimensional solid state physics, where one considers a system which is limited in one of the three usual spatial dimensions.
At the limit where the size of the compact dimension goes to zero, no fields depend on this extra dimension, and the theory is dimensionally reduced
Dimensional reduction
In physics, a theory in D spacetime dimensions can be redefined in a lower number of dimensions d, by taking all the fields to be independent of the location in the extra D − d dimensions....
.

Compactification in string theory
In string theory, compactification is a generalization of Kaluza–Klein theoryKaluza–Klein theory
In physics, Kaluza–Klein theory is a model that seeks to unify the two fundamental forces of gravitation and electromagnetism. The theory was first published in 1921. It was proposed by the mathematician Theodor Kaluza who extended general relativity to a five-dimensional spacetime...
. It tries to conciliate the gap between the conception of our universe based on its four observable dimensions with the ten, eleven, or twenty-six dimensions theoretical equations lead to suppose the universe is made with. For this purpose it is assumed the extra dimensions are "wrapped" up on themselves, or "curled" up on Calabi–Yau spaces, or on orbifold
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
s. Models in which the compact directions support flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
es are known as flux compactifications. The coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
of string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, which determines the probability of strings to split and reconnect, can be described by a field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
called dilaton
Dilaton
In particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
. This in turn can be described as the size of an extra (eleventh) dimension which is compact. In this way, the ten-dimensional type IIA string theory can be described as the compactification of M-theory
M-theory
In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
in eleven dimensions. Furthermore, different versions of string theory are related by different compactifications in a procedure known as T-duality
T-duality
T-duality is a symmetry of quantum field theories with differing classical descriptions, of which the relationship between small and large distances in various string theories is a special case. Discussion of the subject originated in a paper by T. S. Buscher and was further developed by Martin...
.
The formulation of more precise versions of the meaning of compactification in this context has been promoted by discoveries such as the mysterious duality.
Flux compactification
A flux compactification is a particular way to deal with additional dimensions required by string theory. It assumes that the shape of the internal manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is a Calabi–Yau manifold or generalized Calabi–Yau manifold which is equipped with non-zero values of fluxes, i.e. differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s that generalize the concept of an electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
(see p-form electrodynamics).
The hypothetical concept of the anthropic landscape in string theory follows from a large number of possibilities in which the integers that characterize the fluxes can be chosen without violating rules of string theory. The flux compactifications can be described as F-theory
F-theory
F-theory is a branch of string theory developed by Cumrun Vafa. The new vacua described as F-theory were discovered by Vafa, and it also allowed string theorists to construct new realistic vacua — in the form of F-theory compactified on elliptically fibered Calabi-Yau four-folds...
vacua or type IIB string theory vacua with or without D-brane
D-brane
In string theory, D-branes are a class of extended objects upon which open strings can end with Dirichlet boundary conditions, after which they are named. D-branes were discovered by Dai, Leigh and Polchinski, and independently by Hořava in 1989...
s.

