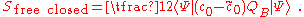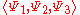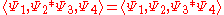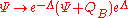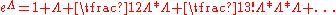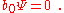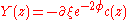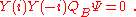String field theory - AbsoluteAstronomy.com

String field theory is a formalism in string theory

String theory

String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...

in which the dynamics of relativistic

Special relativity

Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

strings is reformulated in the language of quantum field theory

Quantum field theory

Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...

. This is accomplished at the level of perturbation theory

Perturbation theory (quantum mechanics)

In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...

by finding a collection of vertices for joining and splitting strings, as well as string propagator

Propagator

In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...

s, that give a Feynman diagram

Feynman diagram

Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...

-like expansion for string scattering amplitudes. In most string field theories, this expansion is encoded by a classical action

Action (physics)

In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...

found by second-quantizing the free string and adding interaction terms. As is usually the case in second quantization, a classical field configuration of the second-quantized theory is given by a wave function in the original theory. In the case of string field theory, this implies that a classical configuration, usually called the string field, is given by an element of the free string Fock space

Fock space

The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...

.

The principal advantages of the formalism are that it allows the computation of off-shell amplitudes

Probability amplitude

In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...

and, when a classical action is available, gives non-perturbative information that cannot be seen directly from the standard genus expansion of string scattering. In particular, following the work of Ashoke Sen

Ashoke Sen

Ashoke Sen , FRS, is an Indian theoretical physicist. He has made a number of major original contributions to the subject of string theory, including his landmark paper on strong-weak coupling duality or S-duality, which was influential in changing the course of research in the field...

, it has been useful in the study of tachyon condensation

Tachyon condensation

In particle physics, theoretical processes that eliminate or resolve particles or fields into better understood phenomena are called, by extension and metaphor with the macroscopic process, "condensation"...

on unstable D-branes. It has also had applications to topological string theory

Topological string theory

In theoretical physics, topological string theory is a simplified version of string theory. The operators in topological string theory represent the algebra of operators in the full string theory that preserve a certain amount of supersymmetry...

, non-commutative geometry, and strings in low dimensions.

String field theories come in a number of varieties depending on which type of string is second quantized: Open string field theories describe the scattering of open strings, closed string field theories describe closed strings, while open-closed string field theories include both open and closed strings.

In addition, depending on the method used to fix the worldsheet diffeomorphisms and conformal transformations in the original free string theory, the resulting string field theories can be very different. Using light cone gauge

Light cone gauge

In theoretical physics, light cone gauge is an approach to remove the ambiguities arising from a gauge symmetry. While the term refers to several situations, a null component of a field A is set to zero in all cases.-Gauge theory:In gauge theory, light-cone gauge refers to the condition A^+=0...

, yields light-cone string field theories whereas using BRST quantization

BRST quantization

In theoretical physics, BRST quantization is a relatively rigorous mathematical approach to quantizing a field theory with a gauge symmetry...

, one finds covariant string field theories. There are also hybrid string field theories, known as covariantized light-cone string field theories which use elements of both light-cone and BRST gauge-fixed string field theories.

A final form of string field theory, known as background independent open string field theory, takes a very different form; instead of second quantizing the worldsheet string theory, it second quantizes the space of two-dimensional quantum field theories.

Light-cone string field theory

Light-cone string field theories were introduced by Stanley Mandelstam

Stanley Mandelstam

Stanley Mandelstam is a South African-born theoretical physicist. He introduced the relativistically invariant Mandelstam variables into particle physics in 1958 as a convenient coordinate system for formulating his double dispersion relations...

and developed by Mandelstam, Michael Green

Michael Green (physicist)

Michael Boris Green FRS is a British physicist and one of the pioneers of string theory. Currently a professor in the Department of Applied Mathematics and Theoretical Physics and a Fellow in Clare Hall at the University of Cambridge in England, he succeeded Stephen Hawking on 1 November 2009...

, John Schwarz and Lars Brink. An explicit description of the second-quantization of the light-cone string was given by Michio Kaku

Michio Kaku

is an American theoretical physicist, the Henry Semat Professor of Theoretical Physics in the City College of New York of City University of New York, the co-founder of string field theory, and a "communicator" and "popularizer" of science...

and Keiji Kikkawa.

Light-cone string field theories were the first string field theories to be constructed and are based on the simplicity of string scattering in light-cone gauge. For example, in the bosonic closed string

Bosonic string theory

Bosonic string theory is the original version of string theory, developed in the late 1960s.In the early 1970s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory became the real focus...

case, the worldsheet scattering diagrams naturally take a Feynman diagram-like form, being built from two ingredients, a propagator

Propagator

and two vertices for splitting and joining strings, which can be used to glue three propagators together,

These vertices and propagators produce a single cover of the moduli space of

-point closed string scattering amplitudes so no higher order vertices are required. Similar vertices exist for the open string.

When one considers light-cone quantized superstrings, the discussion is more subtle as divergences can arise when the light-cone vertices collide. To produce a consistent theory, it is necessary to introduce higher order vertices, called contact terms, to cancel the divergences.

Light-cone string field theories have the disadvantage that they break manifest Lorentz invariance. However, in backgrounds with light-like killing vectors

Killing vector field

In mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...

, they can considerably simplify the quantization of the string action. Moreover, until the advent of the Berkovits string it was the only known method for quantizing strings in the presence of Ramond-Ramond field

Ramond-Ramond field

In theoretical physics, Ramond–Ramond fields are differential form fields in the 10-dimensional spacetime of type II supergravity theories, which are the classical limits of type II string theory. The ranks of the fields depend on which type II theory is considered...

s. In recent research, light-cone string field theory played an important role in understanding strings in pp-wave backgrounds.

Free covariant string field theory

An important step in the construction of covariant string field theories (preserving manifest Lorentz invariance) was the construction of a covariant kinetic term. This kinetic term can be considered a string field theory in its own right: the string field theory of free strings. Since the work of Warren Siegel, it has been standard to first BRST-quantize the free string theory and then second quantize so that the classical fields of the string field theory include ghosts as well as matter fields. For example, in the case of the bosonic open string theory in 26-dimensional flat spacetime, a general element of the Fock-space of the BRST quantized string takes the form (in radial quantization in the upper half plane),

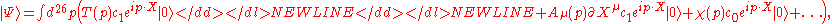
where

is the free string vacuum and the dots represent more massive fields. In the language of worldsheet string theory,

, and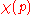

represent the amplitudes for the string to be found in the various basis states. After second quantization, they are interpreted instead as classical fields representing the tachyon

, gauge field

and a ghost field

.

In the worldsheet string theory, the unphysical elements of the Fock space are removed by imposing the condition

as well as the equivalence relation

. After second quantization, the equivalence relation is interpreted as a gauge invariance, whereas the condition that

is physical is interpreted as an equation of motion

Equation of motion

Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...

. Because the physical fields live at ghostnumber one, it is also assumed that the string field

is a ghostnumber one element of the Fock space.

In the case of the open bosonic string a gauge-unfixed action with the appropriate symmetries and equations of motion was originally obtained by André Neveu

André Neveu

André Neveu is a French physicist working on string theory and quantum field theory who coinvented the Neveu-Schwarz algebra and the Gross-Neveu model.Neveu studied in Paris at the École normale supérieure...

, Hermann Nicolai and Peter C. West. It is given by

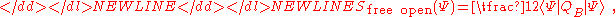
where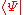

is the BPZ-dual of

.

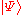For the bosonic closed string, construction of a BRST-invariant kinetic term requires additionally that one impose

and

. The kinetic term is then

Additional considerations are required for the superstrings to deal with the superghost zero-modes.

Witten's cubic open string field theory

The best studied and simplest of covariant interacting string field theories was constructed by Edward Witten

Edward Witten

Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....

. It describes the dynamics of bosonic open strings and is given by adding to the free open string action a cubic vertex:

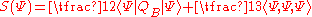where, as in the free case,

is a ghostnumber one element of the BRST-quantized free bosonic open-string Fock-space.

The cubic vertex,

is a triliniar map which takes three string fields of total ghostnumber three and yields a number.
Following Witten, who was motivated by ideas from noncommutative geometry, it is conventional to introduce the

-product defined implicitly through

The

-product and cubic vertex satisfy a number of important properties (allowing the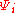

to be general ghost number fields):

Cyclicity :
BRST invariance :

For the -product, this implies that acts as a graded derivation
Associativity

In terms of the cubic vertex,

In these equations,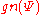

denotes the ghost number of

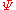Gauge invariance

These properties of the cubic vertex are sufficient to show that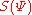

is invariant under
the Yang-Mills-like gauge transformation,

where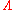

is an infinitesimal gauge parameter. Finite gauge transformations take the form

where the exponential is defined by,

Equations of motion

The equations of motion are given by

Because the string field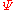

is an infinite collection of ordinary classical fields, these equations represent an infinite collection of non-linear coupled differential equations. There have been two approaches to finding solutions: First, numerically, one can truncate the string field to include only fields with mass less than a fixed bound, a procedure known as "level truncation". This reduces the equations of motion to a finite number of coupled differential equations and has led to the discovery of many solutions. Second, following the work of Martin Schnabl one can seek analytic solutions by carefully picking an ansatz which has simple behavior under star multiplication and action by the BRST operator. This has led to solutions representing marginal deformations as well as the tachyon vacuum solution

Quantization

To consistently quantize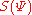

one has to fix a gauge. The traditional choice has been Feynman-Siegel gauge,

Because the gauge transformations are themselves redundant (there are gauge transformations of the gauge transformations), the gauge fixing procedure requires introducing an infinite number of ghosts via the BV formalism

Batalin-Vilkovisky formalism

In theoretical physics, the Batalin–Vilkovisky formalism was developed as a method for determining the ghost structure for Lagrangian gauge theories, such as gravity and supergravity, whose corresponding Hamiltonian formulation has constraints not related to a Lie algebra In theoretical...

. The complete gauge fixed action is given by

where the field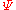

is now allowed to be of arbitrary ghostnumber. In this gauge, the Feynman diagrams are constructed from a single propagator and vertex. The propagator takes the form of a strip of worldsheet of width

and length

There is also an insertion of an integral of the

-ghost along the red line. The modulus,

is integrated from 0 to

.

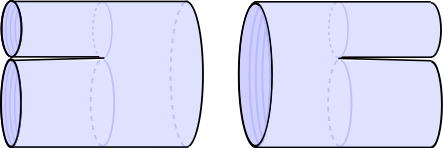
The three vertex can be described as a way of gluing three propagators together as shown in the following picture:

In order to represent the vertex embedded in three dimensions, the propagators have been folded in half along their midpoints. The resulting geometry is completely flat except for a single curvature singularity where the midpoints of the three propagators meet.

These Feynman diagrams generate a complete cover of the moduli space of open string scattering diagrams. It follows that, for on-shell amplitudes, the n-point open string amplitudes computed using Witten's open string field theory are identical to those computed using standard worldsheet methods.

Supersymmetric covariant open string field theories

There are two main constructions of supersymmetric extensions of Witten's cubic open string field theory. The first is very similar in form to its bosonic cousin and is known as modified cubic superstring field theory. The second, due to Nathan Berkovits is very different and is based on a WZW

Wess-Zumino-Witten model

In theoretical physics and mathematics, the Wess–Zumino–Witten model, also called the Wess–Zumino–Novikov–Witten model, is a simple model of conformal field theory whose solutions are realized by affine Kac–Moody algebras...

-type action.

Modified cubic superstring field theory

The first consistent extension of Witten's bosonic open string field theory to the RNS string was constructed by
Christian Preitschopf, Charles Thorn and Scott Yost and independently by Irina Aref'eva, P. B. Medvedev and A. P. Zubarev. The NS string field is taken to be a ghostnumber one picture zero string field in the small Hilbert space (i.e.

).
The action takes a very similar form to bosonic action,

where

is the inverse picture changing operator. The suggested

picture number extension of this theory to the Ramond sector might be problematic.

This action has been shown to reproduce tree-level amplitudes and has a tachyon vacuum solution with the correct energy.
The one subtlety in the action is the insertion of picture changing operators at the midpoint, which imply that the linearized equations of motion take the form

Because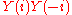

has a non-trivial kernel, there are potentially extra solutions that are not in the cohomology of

. However, such solutions would have operator insertions near the midpoint and would be potentially singular, and importance of this problem remains unclear.

Berkovits superstring field theory

A very different supersymmetric action for the open string was constructed by Nathan Berkovits. It takes the form

where all of the products are performed using the

-product including the anticommutator

, and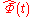

is any string field such that

and

. The string field

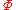is taken to be in the NS sector of the large Hilbert space, i.e. including the zero mode of

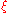. It is not known how to incorporate the R sector, although some preliminary ideas exist.

The equations of motion take the form

The action is invariant under the gauge invariance

The principal advantage of this action is that it free from any insertions of picture-changing operators. It has been shown to reproduce correctly tree level amplitudes and has been found, numerically, to have a tachyon vacuum with appropriate energy. The only known analytic solutions to the classical equations of motion are marginal deformations.

Other formulations of covariant open superstring field theory

A formulation of superstring field theory using the non-minimal pure-spinor variables was introduced by Berkovits. The action is cubic and includes a mid-point insertion whose kernel is trivial. As always within the pure-spinor formulation, the Ramond sector can be easily treated. However, it is not known how to incorporate the GSO- sectors into the formalism.

In an attempt to resolve the allegedly problematic mid-point insertion of the modified cubic theory, Berkovits and Siegel proposed a superstring field theory based on a non-minimal extension of the RNS string, which uses a mid-point insertion with no kernel. It is not clear if such insertions are in any way better than mid-point insertions with non-trivial kernels.

Covariant closed string field theory

Covariant closed string field theories are considerably more complicated than their open string cousins. Even if one wants to construct a string field theory which only reproduces tree-level interactions between closed strings, the classical action must contain an infinite number of vertices consisting of string polyhedra.

If one demands that on-shell scattering diagrams be reproduced to all orders in the string coupling, one must also include additional vertices arising from higher genus (and hence higher order in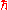

) as well. In general, a manifestly BV invariant, quantizable action takes the form

where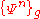

denotes an

th order vertex arising from a genus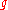

surface and

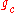is the closed string coupling. The structure of the vertices is in principle determined by a minimal area prescription, although, even for the polyhedral vertices, explicit computations have only been performed to quintic order.

Covariant heterotic string field theory

A formulation of the NS sector of the heterotic string was given by Berkovits, Okawa and Zwiebach.
The formulation amalgams bosonic closed string field theory with Berkovits' superstring field theory.

Light-cone string field theory

Free covariant string field theory

Witten's cubic open string field theory

Gauge invariance

Equations of motion

Quantization

Supersymmetric covariant open string field theories

Modified cubic superstring field theory

Berkovits superstring field theory

Other formulations of covariant open superstring field theory

Covariant closed string field theory

Covariant heterotic string field theory

See also