Seesaw mechanism
Encyclopedia
In theoretical physics
, the seesaw mechanism is a mechanism within grand unification theory
, and in particular in theories of neutrino
masses and neutrino oscillation
, where it can be used to explain the smallness of observed neutrino masses relative to those of quark
s and lepton
s.
There are several varieties commonly referred to as type 1 seesaw, type 2 seesaw etc. The simplest version, type 1, requires as additional assumptions to the standard model
only two or more right-handed neutrino fields, and the existence of a very large mass scale in the theory which can for example be the scale of grand unification.
, which has possibly been detected.
The mathematics behind the seesaw mechanism is the following fact: the 2×2 matrix
where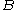
is much larger than 
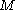, has the following eigenvalues: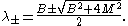
The larger eigenvalue is approximately equal to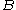
while the smaller eigenvalue is approximately equal to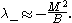
Therefore, M is the geometric mean
of B and λ−, up to the sign. In other words, the determinant
equals . If one of the eigenvalues goes up, the other goes down, and vice versa. This is the reason why the name seesaw
was given to the mechanism.
This mechanism is used to explain why the neutrino
masses are so small. The matrix A is essentially the mass matrix
for the right-handed neutrino. The Majorana mass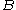
is comparable to the GUT scale and M, the Dirac mass, is of order of the electroweak scale. The smaller eigenvalue then leads to a very small neutrino mass comparable to which qualitatively agrees with the experiments. Such an agreement may be interpreted as an experimentally confirmed qualitative prediction of Grand Unified Theories.
by considering the most general mass matrix allowed by gauge invariance
of the standard model action
, and the corresponding charges of the lepton- and neutrino fields. Let the Weyl spinor χ be the neutrino
part of a left-handed
lepton
isospin
doublet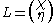
as it is present in the minimal standard model
without neutrino masses, and let η be a postulated right-handed neutrino Weyl spinor which is a singlet under weak isospin
. There are now three ways to form Lorentz covariant
mass terms, giving either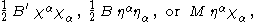
and their complex conjugate
s, which can be written as a quadratic form
,
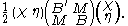
Since the right-handed neutrino spinor is uncharged under all standard model gauge symmetries, B is a free parameter which can in principle take any arbitrary value. The parameter M is forbidden by electroweak gauge symmetry
, and can only appear after its spontaneous breakdown
through a Higgs mechanism
. In particular, since has weak isospin
½ like the Higgs field H, and χ has weak isospin
0, the mass parameter M can be generated from Yukawa interaction
s with the Higgs field,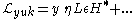
This means that M is naturally
of the order of the vacuum expectation value
of the standard model Higgs field,
if the dimensionless Yukawa coupling
is . It can be chosen smaller consistently, but extreme values can make the model nonperturbative
. The parameter B on the other hand, is completely forbidden, since no singlet under weak hypercharge
and isospin
can be formed using these objects. This is the origin of the pattern and hierarchy of scales of the mass matrix A within the "type 1" seesaw mechanism. The exact size of B can be explained in the context of grand unification
. In such models, enlarged gauge symmetries
may be present which initially force in the unbroken phase, but generate a nonvanishing value around the scale of their spontaneous symmetry breaking
.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the seesaw mechanism is a mechanism within grand unification theory
Grand unification theory
The term Grand Unified Theory, often abbreviated as GUT, refers to any of several similar candidate models in particle physics in which at high-energy, the three gauge interactions of the Standard Model which define the electromagnetic, weak, and strong interactions, are merged into one single...
, and in particular in theories of neutrino
Neutrino
A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
masses and neutrino oscillation
Neutrino oscillation
Neutrino oscillation is a quantum mechanical phenomenon predicted by Bruno Pontecorvowhereby a neutrino created with a specific lepton flavor can later be measured to have a different flavor. The probability of measuring a particular flavor for a neutrino varies periodically as it propagates...
, where it can be used to explain the smallness of observed neutrino masses relative to those of quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s and lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
s.
There are several varieties commonly referred to as type 1 seesaw, type 2 seesaw etc. The simplest version, type 1, requires as additional assumptions to the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
only two or more right-handed neutrino fields, and the existence of a very large mass scale in the theory which can for example be the scale of grand unification.
Type 1 seesaw
This model produces a light neutrino, corresponding to the three known neutrino flavors, and a very heavy, undiscovered sterile neutrinoSterile neutrino
Sterile neutrinosIn scientific literature, these particles are also variously referred to as right-handed neutrinos, inert neutrinos, heavy neutrinos, or neutral heavy leptons . are a hypothetical type of neutrino that do not interact via any of the fundamental interactions of the Standard Model...
, which has possibly been detected.
The mathematics behind the seesaw mechanism is the following fact: the 2×2 matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
where
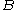is much larger than 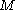, has the following eigenvalues: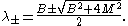The larger eigenvalue is approximately equal to
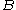while the smaller eigenvalue is approximately equal to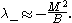Therefore, M is the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
of B and λ−, up to the sign. In other words, the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
equals . If one of the eigenvalues goes up, the other goes down, and vice versa. This is the reason why the name seesaw
Seesaw
A seesaw is a long, narrow board pivoted in the middle so that, as one end goes up, the other goes down.-Mechanics:Mechanically a seesaw is a lever and fulcrum....
was given to the mechanism.
This mechanism is used to explain why the neutrino
Neutrino
A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
masses are so small. The matrix A is essentially the mass matrix
Mass matrix
In computational mechanics, a mass matrix is a generalization of the concept of mass to generalized coordinates. For example, consider a two-body particle system in one dimension...
for the right-handed neutrino. The Majorana mass
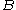is comparable to the GUT scale and M, the Dirac mass, is of order of the electroweak scale. The smaller eigenvalue then leads to a very small neutrino mass comparable to which qualitatively agrees with the experiments. Such an agreement may be interpreted as an experimentally confirmed qualitative prediction of Grand Unified Theories.Field Theory Background
The 2×2 matrix A arises in a natural manner within the standard modelStandard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
by considering the most general mass matrix allowed by gauge invariance
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
of the standard model action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
, and the corresponding charges of the lepton- and neutrino fields. Let the Weyl spinor χ be the neutrino
Neutrino
A neutrino is an electrically neutral, weakly interacting elementary subatomic particle with a half-integer spin, chirality and a disputed but small non-zero mass. It is able to pass through ordinary matter almost unaffected...
part of a left-handed
Chirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
lepton
Lepton
A lepton is an elementary particle and a fundamental constituent of matter. The best known of all leptons is the electron which governs nearly all of chemistry as it is found in atoms and is directly tied to all chemical properties. Two main classes of leptons exist: charged leptons , and neutral...
isospin
Weak isospin
In particle physics, weak isospin is a quantum number relating to the weak interaction, and parallels the idea of isospin under the strong interaction. Weak isospin is usually given the symbol T or I with the third component written as Tz, T3, Iz or I3...
doublet
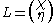
as it is present in the minimal standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
without neutrino masses, and let η be a postulated right-handed neutrino Weyl spinor which is a singlet under weak isospin
Weak isospin
In particle physics, weak isospin is a quantum number relating to the weak interaction, and parallels the idea of isospin under the strong interaction. Weak isospin is usually given the symbol T or I with the third component written as Tz, T3, Iz or I3...
. There are now three ways to form Lorentz covariant
Lorentz covariance
In standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
mass terms, giving either
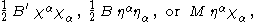
and their complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
s, which can be written as a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
,
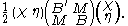
Since the right-handed neutrino spinor is uncharged under all standard model gauge symmetries, B is a free parameter which can in principle take any arbitrary value. The parameter M is forbidden by electroweak gauge symmetry
Electroweak interaction
In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
, and can only appear after its spontaneous breakdown
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
through a Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
. In particular, since has weak isospin
Weak isospin
In particle physics, weak isospin is a quantum number relating to the weak interaction, and parallels the idea of isospin under the strong interaction. Weak isospin is usually given the symbol T or I with the third component written as Tz, T3, Iz or I3...
½ like the Higgs field H, and χ has weak isospin
Weak isospin
In particle physics, weak isospin is a quantum number relating to the weak interaction, and parallels the idea of isospin under the strong interaction. Weak isospin is usually given the symbol T or I with the third component written as Tz, T3, Iz or I3...
0, the mass parameter M can be generated from Yukawa interaction
Yukawa interaction
In particle physics, Yukawa's interaction, named after Hideki Yukawa, is an interaction between a scalar field \phi and a Dirac field \Psi of the typeV \approx g\bar\Psi \phi \Psi or g \bar \Psi \gamma^5 \phi \Psi ....
s with the Higgs field,
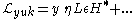
This means that M is naturally
Naturalness (physics)
Naturalness is the property that all parameters appearing in a theory take values of order 1...
of the order of the vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of the standard model Higgs field,
if the dimensionless Yukawa coupling
Yukawa interaction
In particle physics, Yukawa's interaction, named after Hideki Yukawa, is an interaction between a scalar field \phi and a Dirac field \Psi of the typeV \approx g\bar\Psi \phi \Psi or g \bar \Psi \gamma^5 \phi \Psi ....
is . It can be chosen smaller consistently, but extreme values can make the model nonperturbative
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
. The parameter B on the other hand, is completely forbidden, since no singlet under weak hypercharge
Weak hypercharge
The weak hypercharge in particle physics is a conserved quantum number relating the electrical charge and the third component of weak isospin, and is similar to the Gell-Mann–Nishijima formula for the hypercharge of strong interactions...
and isospin
Weak isospin
In particle physics, weak isospin is a quantum number relating to the weak interaction, and parallels the idea of isospin under the strong interaction. Weak isospin is usually given the symbol T or I with the third component written as Tz, T3, Iz or I3...
can be formed using these objects. This is the origin of the pattern and hierarchy of scales of the mass matrix A within the "type 1" seesaw mechanism. The exact size of B can be explained in the context of grand unification
Grand unification theory
The term Grand Unified Theory, often abbreviated as GUT, refers to any of several similar candidate models in particle physics in which at high-energy, the three gauge interactions of the Standard Model which define the electromagnetic, weak, and strong interactions, are merged into one single...
. In such models, enlarged gauge symmetries
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
may be present which initially force in the unbroken phase, but generate a nonvanishing value around the scale of their spontaneous symmetry breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
.